
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Методы прогнозирования проявления опасных климатических явлений
Профессор В.У.Стоянов
И.о. доцента М.В.Бакулина
Значительная часть явлений природы (чрезвычайные ситуации природного характера) протекают при существенном участии тех или иных случайных факторов. Если знать вероятность проявления опасных природных явлений и ожидаемую величину ущерба от них, то можно принять ряд адекватных мер по недопущению или ослаблению воздействия поражающих факторов, ослабить их воздействие благодаря принятию альтернативных решений, предусмотреть эффективные компенсационные механизмы.
Поэтому главной задачей при прогнозировании природных чрезвычайных ситуаций является оценка возможного риска проявления и развития опасных явлений.
Процесс прогнозирования природных катастроф чаще всего основан на использовании долговременных статистических данных наблюдения за теми или иными природными явлениями.
В зависимости от механизма и природы происхождения природные явления классифицируются по классам (рис. 1.1).
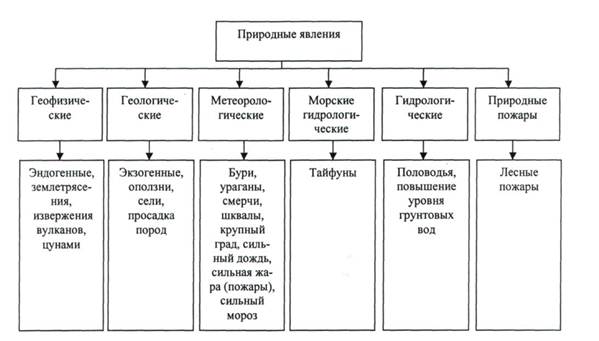
Рис. 1.1. Классификация природных явлений по классам.
Нами будут рассмотрены климатические показатели различных метеорологических явлений. Не перечисляя всех конкретных задач по использованию климатических показателей в различных областях народного хозяйства, укажем их основные типы.
Основное назначение климатических показателей состоит в учете их при перспективном планировании различного рода хозяйственных мероприятий и конструировании различных сооружений и изделий. Планирование и конструирование не может проводиться без учета вероятности проявления опасных климатических явлений и возможных предельных значении их поражающих (негативных) значений.
Метеорологические опасные явления могут быть вызваны следующими причинами:
- ветром, в том числе бурей, ураганом, смерчем при скорости ветра 15 м/с и более;
- сильным дождем (при количестве осадков 50 мм и более в течение 12 часов и более, а в горных, селевых и ливнеопасных районах – 30 мм и более за 12 часов);
- крупным градом (при диаметре градин 20 мм и более);
- сильным снегопадом (при количестве осадков 20 мм и более за 12 часов);
- понижением, повышением температуры воздуха больше принятых в СНиП.
Значительное количество опасных событий (чрезвычайных ситуаций природного характера) протекает при существенном участии тех или иных случайных климатических факторов, причем только часть из них может оказать существенное негативное воздействие. Поэтому, главной задачей прогнозирования чрезвычайных ситуаций природного характера является оценка вероятности проявления и параметров данных негативных метеорологических факторов на данной территории.
| Методы прогнозирования опасных событий природного и техногенного характера значительно различаются. |
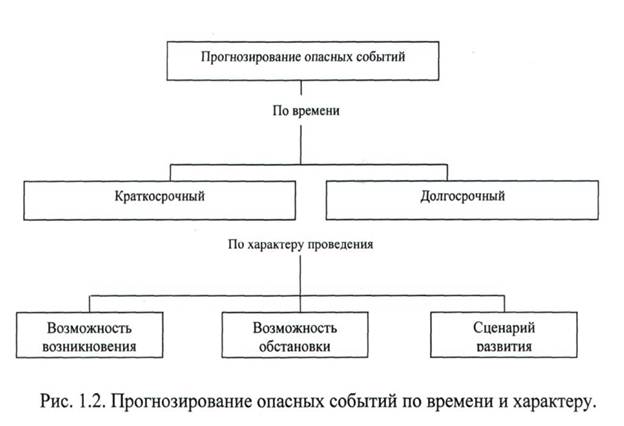 |
Способы прогнозирования опасных событий по времени и характеру проявления классифицируются следующим образом:
Рассмотрим подходы к прогнозированию природных чрезвычайных ситуаций.
Процесс прогнозирования природных катастроф чаще всего основан на использовании долговременных статистических данных наблюдений за теми или иными природными явлениями, проводимых в системе мониторинга состояния окружающей среды. Следует, однако, иметь в виду, что в тот конкретный промежуток времени, на который проводится прогнозирование, фактические условия могут существенно отличаться от среднестатистических. Просто надо понимать, что имеющиеся статистические показатели служат лишь фоном, который используется для несвойственной ему функции ориентира на возможность проявления опасного природного фактора в настоящее время или в ближайшем будущем. И такой подход к прогнозу чрезвычайных ситуаций природного характера на практике себя хорошо оправдывает. При этом неразумно, с одной стороны, предъявлять слишком большие требования к точности получаемых прогнозных показателей опасных природных явлений. С другой стороны, задачи прогноза опасности для населения и территорий – это такие задачи, когда требуется как можно точнее охарактеризовать возможные риски в конкретном районе или в конкретный отрезок времени. При решении таких задач необходимо стремиться к получению статистических данных с наибольшей возможной точностью.
При таком подходе прогнозирование возможностей риска возникновения опасного природного фактора на данный момент времени в данном конкретном районе по исходным данным, приведенным в таблицах справочной литературы, путем расчета всегда является трудоемкой и длительной операцией. В то же время, рассматривая ряды статистических наблюдений за геологическими, гидрологическими и метеорологическими факторами как ряда случайных величин, можно использовать уже установленные законы распределения этих случайных величин, что во многом облегчает прогноз оценки риска возникновения той или иной чрезвычайной ситуации в данный период времени на данной территории.
Практически задача состоит в том, чтобы продлить уже имеющиеся статистические зависимости распределения случайного фактора в области с маловероятностными значениями. При этом не требуется точного теоретического обоснования предлагаемого отрезка для продлевания функции. Достаточно лишь вычислить некоторые количественные критерии соответствия предлагаемого теоретического распределения эмпирическим данным. При этом вероятностные показатели любого опасного фактора в этом случае могут быть получены с достаточно большой точностью без особого труда и без обращения к исходному ряду наблюдений, что очень важно для прогнозирования относительно редко возникающих опасных природных явлений.
Наиболее простым законом распределения дискретной случайной величины является классический биноминальный закон, установленный Бернулли.Метеорологическое явление, описываемое биноминальным распределением, может принимать значения 
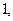
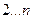 с вероятностью:
с вероятностью:
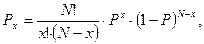
| (1.1) |
где:  - означает вероятность осуществления данного случайного события,
- означает вероятность осуществления данного случайного события, 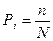 ;
;
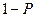 - вероятность неосуществления этого события;
- вероятность неосуществления этого события;
 - число дней, при которых обычно проявляется изучаемое явление на данной территории (статистический показатель метеонаблюдений за значительный промежуток времени);
- число дней, при которых обычно проявляется изучаемое явление на данной территории (статистический показатель метеонаблюдений за значительный промежуток времени);
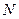 - число дней в изучаемом временном промежутке (месяце);
- число дней в изучаемом временном промежутке (месяце);
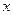 - прогнозируемое время (1, 2, 3 дня) проявления опасного явления.
- прогнозируемое время (1, 2, 3 дня) проявления опасного явления.
Каждое значение случайной величины, распределенной по биноминальному закону, следует понимать как число случаев осуществления некоторого случайного события из  возможных случаев. В метеорологии таким событием может быть день с опасным явлением, декада или месяц, имеющие опасные условия, характерные для начала негативных процессов. Например, сухой месяц – возникновение природных пожаров, гибель урожая от засухи и др.; влажный месяц – подтопления, оползни, селевые потоки и др.
возможных случаев. В метеорологии таким событием может быть день с опасным явлением, декада или месяц, имеющие опасные условия, характерные для начала негативных процессов. Например, сухой месяц – возникновение природных пожаров, гибель урожая от засухи и др.; влажный месяц – подтопления, оползни, селевые потоки и др.
Для выравнивания статистически наблюденного распределения по биноминальному закону необходимо, прежде всего, найти параметры этого закона  и
и  . Обычно,
. Обычно,  задается числом дней. Вероятность случайного метеорологического явления вычисляется как отношение числа дней с опасным явлением ко всему числу случаев наблюдений
задается числом дней. Вероятность случайного метеорологического явления вычисляется как отношение числа дней с опасным явлением ко всему числу случаев наблюдений  . Например, если в данном месяце (продолжительностью 30 дней) в среднем наблюдается 3 дня с опасным явлением, то
. Например, если в данном месяце (продолжительностью 30 дней) в среднем наблюдается 3 дня с опасным явлением, то 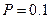 . По формуле (1.1) рассчитывают вероятности различного числа дней с опасным явлением, из которых и формируется биноминальное распределение, выравнивающее наблюденное распределение.
. По формуле (1.1) рассчитывают вероятности различного числа дней с опасным явлением, из которых и формируется биноминальное распределение, выравнивающее наблюденное распределение.
Можно ожидать, что биноминальному распределению в некоторых случаях будет подчиняться распределение числа дней с такими опасными метеорологическими явлениями как грозы, туман, метель за сравнительно короткие промежутки времени (декаду, месяц).
Для определения ветровых нагрузок используют скорости ветра заданной обеспеченности, иначе говоря, наибольшие скорости, возможные определенное количество раз в заданное число лет. В зависимости от типа сооружения, от проектируемой продолжительности его существования может быть задана обеспеченность (интегральная повторяемость), с которой наблюдается опасная скорость ветра. Интегральная кривая повторяемости, настроенная по результатам обработки всей совокупности наблюдений над ветром за многолетний период, аппроксимируется аналитической функцией вида:

| (1.2) |
 где:
где:  - число лет, за которые один раз наблюдалась скорость ветра, равная или превосходящая величину
- число лет, за которые один раз наблюдалась скорость ветра, равная или превосходящая величину 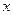 ;
;
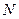 - число наблюдений в течение года, которая является частным случаем функции Гудригаи широко применяется в гидрологических расчетах [14].
- число наблюдений в течение года, которая является частным случаем функции Гудригаи широко применяется в гидрологических расчетах [14].
Интегральные повторяемости скорости ветра рассчитываются по дифференциальным повторяемостям, содержащимся в справочной литературе и наносятся на номограмму, представленную на рис. 1.3.

Рис. 1.3. Интегральные повторяемости скорости ветра.
На этой номограмме интегральная кривая достаточно хорошо спрямляется и с нее снимаются требуемые значения расчетных скоростей ветра. В качестве примера на номограмме нанесены интегральные повторяемости, рассчитанные по наблюдениям метеостанции Черноморская АР Крым.
Поскольку интегральные повторяемости рассчитывались по всей совокупности четырехстрочных наблюдений, то число их в году равно 1461. Полагая  и задавая значения
и задавая значения  , легко определить значения
, легко определить значения  ,соответствующие различным периодам повторения. Так, например, интегральная повторяемость скорости ветра, возможной раз в году, будет равна
,соответствующие различным периодам повторения. Так, например, интегральная повторяемость скорости ветра, возможной раз в году, будет равна  или
или 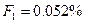 . Положив
. Положив  годам, найдем соответствующие значения
годам, найдем соответствующие значения  равные
равные 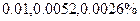 . По этим значениям повторяемости с интегральной кривой, нанесенной на номограмму, легко снимаются требуемые расчетные скорости.
. По этим значениям повторяемости с интегральной кривой, нанесенной на номограмму, легко снимаются требуемые расчетные скорости.
| <== предыдущая страница | | | следующая страница ==> |
| Принятие управленческих решений по снижению уровня риска | | | Методы прогнозирования проявления опасных геологических явлений |
Дата добавления: 2014-03-22; просмотров: 1817; Нарушение авторских прав

Мы поможем в написании ваших работ!