Перевычисляют измеренные плоские координаты ИСЗ в экваториальные на эпоху измерений

Для того, чтобы выбрать из каталога координаты звезд, полученные на снимке, эти звезды необходимо опознать. Процесс опознавания называется отождествлением и выполняется визуально при помощи различных звездных атласов путем сличения конфигураций звезд на снимке и в атласе.

После отождествления звезд на снимке, измеряют их координаты и координаты ИСЗ с помощью высокоточной координатно-измерительной машины. Затем в экваториальные координаты звезд вводят поправки за рефракцию и годичную аберрацию.

а) Поправка за аберрацию:

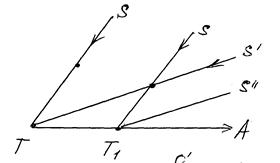
Предположим, что в момент

фотографирования спутника Т,

получены его координаты. Эти

координаты необходимо относить не к моменту Т, а к другому моменту Т’. Разность между моментами Т и Т’ вызвана влиянием спутниковой аберрации и называется аберрационным временем:

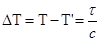, где τ- расстояние до ИСЗ, с-скорость света.

При обработке наблюдений, поправкой за аберрацию не обязательно исправлять момент Т. Ее можно учесть, исправляя непосредственно значения прямого восхождения и склонения ИСЗ.

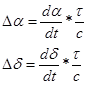значения скоростей 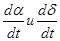можно получить из обработки

Негативов, используя прерывистые следы изображений спутников и производя соответствующие измерения.

б) Поправка за рефракцию:

Рефракция- это явление преломления световых лучей, проходящих через воздушные слои различной плотности. Выделить слои невозможно, т.к. воздух сжимаем и на различных расстояниях по высоте, его плотность различна. Поэтому считают, что свет бесконечно много раз преломляется в атмосфере и луч представляет собой кривую большого радиуса.

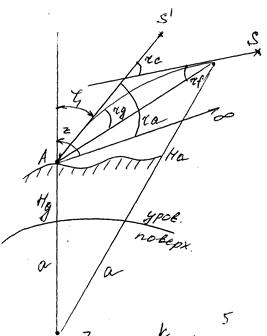
В зависимости от положения источника и приемника световых волн различают следующие виды рефракции:

ζ-измеренное зенитное расстояние

Н_а- высота источника света над уровен-

ной поверхностью в момент начала

преломления

Н_g- высота над уровенной поверхностью

приемника световых волн

а- радиус Земли

.

τ_А- астрономическая рефракция. Источник света в бесконечности, приемник на поверхности Земли.

τ_с- полная рефракция: угол между касательными, проведенными к траектории светового луча в начальной и конечной точках преломления света.

τ_g- Земная (планетная) рефракция: источник света в атмосфере или за его пределами, но на конечном расстоянии (например, ИСЗ), приемник на поверхности Земли.

τ_f- фотограмметрическая (параллактическая) рефракция: источник света на поверхности Земли, приемник в атмосфере или за ее пределами, но на конечном расстоянии.

Кроме перечисленных имеются еще: нормальная (средняя) рефракция: среднее значение, изменяющегося со временем в зависимости от метеорологических условий, угла рефракции на данном зенитном расстоянии; случайная рефракция: низкочастотные изменения рефракции с частотой около 0,01 герц; аномальная рефракция: случайные длительно существующие отклонения значений угла рефракции от нормальных на данном зенитном расстоянии.

Наиболее исследованными являются астрономическая и Земная рефракции.

При наблюдении ИСЗ может возникнуть необходимость учета всех видов рефракции, но наиболее вероятным является учет Земной рефракции, т.к. ИСЗ находится хотя и на большом, но все же конечном расстоянии от Земли.

Тогда для ИСЗ найдем: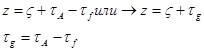

Для определения τ_А (для сферической атмосферы) получен интеграл рефракции:

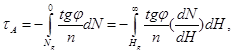где n-коэффициент преломления воздуха на поверхности Земли; N_g- индекс преломления 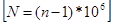в точке наблюдений; φ- угол падения светового луча на границу атмосферы.

Если решить этот интеграл путем разложения в ряд подынтегральной функции, то получим:

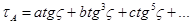
Где а,b,с – коэффициенты, зависящие от метеоусловий атмосферы в пункте наблюдений ( температура, давление, влажность).

Параллактическая (фотограмметрическая) рефракция 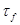для спутника может быть определена по формуле:

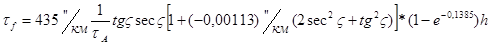
Где h- высота ИСЗ в км; е- основание натурального логарифма.

При h≥1000 км и ζ≤ 45° можно использовать приближенную формулу:

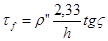, где h- в метрах (высота ИСЗ).

Лекция 13. Связь между плоскими координатами звезд или ИСЗ на снимке с их экваториальными координатами.

В процессе фотографирования, изображения звезд и спутника на снимке, получаются в центральной проекции. Возникает задача перехода от измеренных на снимке прямоугольных координат звезд и ИСЗ к их экваториальным координатам α и δ.

Для получения формул перехода сделаем чертеж:

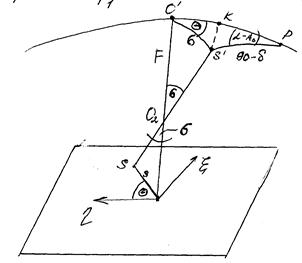
На рис. О- главная точка снимка

О’- точка на небесной сфере, которой

соответствует точка О на снимке.

OS=s- расстояние от главной точки

Снимка до изображения ИСЗ на снимке.

S’- ИСЗ; F- фокусное расстояние камеры;

σ- угловое расстояние ИСЗ.

Из рис. следует, что между угловым

расстоянием ИСЗ и его линейным расстоя-

нием существует следующая зависимость:

s=Ftgσ (1)

Зависимость (1) называется законом Тангенса.

Пр обработки фотографических наблюдений ИСЗ возникает задача: по измеренным прямоугольным координатам x, y, z звезд и спутника, а также по известным из каталога координатам α и δ опорных звезд, найти экваториальные топоцентрические координаты ИСЗ: .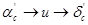

Для решения этой задачи вводится специальная система координат ξ и η с началом в точке О (центр снимка).

Эта система координат называется идеальной или стандарной или тангенциальной. Впервые эти координаты были применены для обработки фотографических наблюдений звезд англ. астрономом Тернером в 1893г.

В идеальной системе ось η совпадает с изображением на снимке круга склонений, а ось ξ ей перпендикулярна.

Тогда, если обозначить координаты оптического центра О через А_{о ,}Д_о, то в единицах фокусного расстояния (F=1) в соответствии с рисунком, получим:

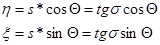(2)

Опустим на сторону О’Р сферический перпендикуляр KS’. Обозначим склонение этого перпендикуляра через q, тогда KP=90-q; O’P=90- Д_о; O’K=q- Д_о. Из прямоугольного треугольника O’KS’ по правилу Непера, получим:

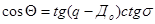(3)

Подставим (3) в первое уравнение системы (2), найдем:

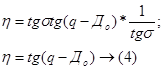
Из того же треугольника, запишем:

Подставим (5) в (2), получим:

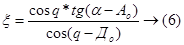
Для определения q из прямоугольного треугольника KPS’:

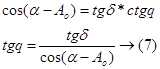,откуда

Формулы (4), (5), (6) позволяют определять идеальные ξ и η координаты ИСЗ через известные экваториальные координаты α и δ – это прямая задача.

Обратная задача- это определение экваториальных координат α и δ спутника по его идеальным координатам ξ и η

Эта задача решается по формулам:

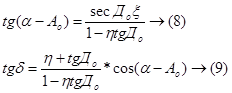
Связь между идеальными координатами спутника (ξ и η) и измеренными на снимке координатами ИСЗ (x, y).

Такая связь устанавливается с помощью уравнений Тернера. Эти уравнения имеют вид:

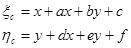
В этих уравнениях a, b, c, d, e, f постоянные (const) пластинки (коэффициенты уравнений Тернера), которые находят из решения нормальных уравнений, если число звезд более 3х.

Обычно при обработке фотографических наблюдений ИСЗ в качестве опорных используют от 6 до 10 звезд.

Порядок вычисления топоцентрических координат ИСЗ по результатам обработки фотографических наблюдений следующий:

1. Отождествление звезд на снимке с помощью звездных атласов;

2. Выборка из каталога координат опорных звезд (α_о и δ_о);

3. Приведение α_о и δ_о от эпохи каталога на момент наблюдений;

4. Определение по опорным звездам положения центра снимка (А_{о ,}Д_о,);

5. Измерение на снимке прямоугольных координат звезд (x, y) и спутника (x_c , y_c) и исправления их за ошибки прибора;

6. Переход от экваториальных координат звезд (α и δ) к их идеальным координатам (ξ и η);

7. Составление для звезд уравнений Тернера и определение a, b, c, d, e, f;

8. Составление уравнений Тернера для ИСЗ и определение ξ_сп и η_сп ;

Дата добавления: 2014-03-24; просмотров: 439; Нарушение авторских прав

Мы поможем в написании ваших работ!