Основные понятия

Аэродинамический расчет воздуховодов обычно сводится к определению размеров их поперечного сечения, а также потерь давления на отдельных участках и системы в целом. Это прямая задача. Возможна и обратная задача – определить расходы воздуха при заданных размерах воздуховодов и известном перепаде давления в системе.

При аэродинамическом расчете воздуховодов систем вентиляции можно пренебречь сжимаемостью перемещающегося воздуха, так как максимально возможное изменение давления в системе меньше 5 % атмосферного. По этой же причине принято пользоваться значениями избыточных давлений, принимая за условный нуль атмосферное давление на уровне системы. Одна из особенностей вентиляционных систем – наличие участков, где избыточное давление меньше нуля.

При движении воздуха по воздуховоду в любом поперечном сечении потока различают три вида давления: статическое, динамическое и полное.

Статическое давление можно рассматривать как потенциальную энергию сжатия 1 м³ воздуха, равную работе, которую может совершить 1 м³ воздуха при расширении.

Динамическое давление – кинетическая энергия, отнесенная к 1 м³ движущегося воздуха, эквивалентная давлению

.

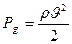Динамическое давление является всегда положительной величиной, оно не меняется при постоянном сечении трубы и зависит только от скорости и плотности перемещаемого воздуха.

Полное давление представляет собой сумму статического и динамического давлений

.

т.е. выражает полный запас энергии движущегося воздуха в рассматриваемом сечении воздуховода.

Потери давления в системе вентиляции складываются из потерь на трение и потерь в местных сопротивлениях.

16.2. Потери давления на трение

Рассмотрим движение воздуха на отрезке воздуховода между сечениями I – I и II – II. Заданы длина отрезка l, площадь поперечного сечения ¦, периметр сечения П и расход воздуха, проходящего через воздуховод L, м³/ч. Статическое давление в сечении I – I равно Р_I, а в сечении II – II – Р_II < Р_I.

Рис. VII.4. Отрезок воздуховода длиной l и диаметром d (J-скорость движения воздуха)

На объем воздуха, заключенного в воздуховоде между рассматриваемыми сечениями, действует сила (Р_I – P_II) ¦, уравновешиваемая силой сопротивления трения воздуха о стенки воздуховода.

Если обозначить касательное напряжение у поверхности стенки, возникающее при движении воздуха, , то силу сопротивления можно определить так: lП. Следовательно, для установившегося движения:

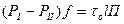; (16.1)

отсюда

. (16.2)

Известно, что касательное напряжение пропорционально динамическому давлению перемещающейся среды

, (16.3)

где y - коэффициент пропорциональности, называемый коэффициентом трения.

Сопоставляя выражения (16.2) и (16.3), получим формулу Вейсбаха

. (16.4)

Отношение f/П для воздуховодов круглого сечения равно 0,25 d, т.е.

. (16.5)

Эта формула предложена Дарси, коэффициент l_тр = 4y называют коэффициентом сопротивления трения. Формула Дарси для воздуховодов с произвольной формой поперечного сечения имеет вид

. (16.6)

Коэффициент сопротивления трения зависит от режима движения и шероховатости стенок воздуховода

,

где Re – критерий Рейнольдса; K – абсолютная шероховатость.

Коэффициент трения определяется по формуле Альтшуля

. (16.7)

При инженерных расчетах потери давления на трение в воздуховоде длиной l, м, принято определять по выражению, Па

, (16.8)

где R – потеря давления на 1 м длины воздуховода, Па/м.

16.3. Эквивалентный диаметр

При расчете воздуховодов вводят понятие эквивалентного диаметра. В практике проектирования получили распространение 3 вида эквивалентных диаметров: по скорости –d_J, по расходу – d_L и по площади поперечного сечения – d_f.

Эквивалентный по скорости диаметр d_Jможно определить из условия, что удельные потери на трение в круглом R и прямоугольном R_пр воздуховодах равны при J = J _пр.

Потери давления на трение в прямоугольном воздуховоде по формуле (16.6)

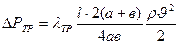. (16.9)

Потери на трение в эквивалентном круглом воздуховоде по формуле (17.5)

. (16.10)

Приравняв выражение (17.9) и (17.10), получим

. (16.11)

Чтобы найти значение R_пр по таблице составленной для круглых воздуховодов, необходимо определить R при d_J и J _пр (фактической скорости в прямоугольном воздуховоде), не принимая во внимание фактический расход воздуха.

Эквивалентный диаметр по расходу d_L определяется из условия, что R = R_пр при равенстве расходов L = L_пр.

Потери на трение в прямоугольном воздуховоде можно выразить через секундный расход воздуха

. (16.12)

Потери на трение в эквивалентном круглом воздуховоде

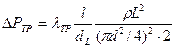. (16.13)

Приравняв выражения (16.12) и (16.13), получим:

;

или

. (16.14)

Чтобы найти значение R_пр по таблице составленной для круглых воздуховодов, необходимо определить R при d_L и L (фактического расхода в прямоугольном воздуховоде), не принимая во внимание фактическую скорость воздуха.

Эквивалентный диаметр по площади поперечного сечения df определяется из условия равенства площадей

. (16.15)

16.4. Потери давления в местных сопротивлениях

Местные сопротивления возникают при изменении направления и скорости движения воздуха (поворот каналов, изменение сечения, тройники, задвижки и т.д.). Коэффициенты местного сопротивления, с точки зрения закона подобия (критерий Эйлера Е = DР / (r), зависят, как и коэффициент трения, от числа Re. Нарушение установившегося поля скоростей начинается на некотором расстоянии до местного сопротивления, а выравнивание потока происходит на некотором расстоянии (обычно несколько калибров – диаметров) после него. На всем участке возмущенного потока происходят потери энергии на вязкое трение и увеличиваются потери на трение о стенки. Однако условно для удобства проведения аэродинамического расчета потери давления в местных сопротивлениях считают сосредоточенными.

Потери давления в местном сопротивлении пропорциональны динамическому давлению воздуха в воздуховоде

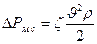. (16.16)

Коэффициент z называется коэффициентом местного сопротивления и определяет потери давления в местном сопротивлении в долях динамического давления. Значения z для различных местных сопротивлений изменяются в широких пределах – обычно 0 < z < 10. В отдельных случаях в ответвлениях тройников возможен отрицательный коэффициент z. Это означает увеличение удельной энергии потока ответвления вследствие эжекции его основным потоком. Таким образом, при расчете изменения давления следует учитывать знак z.

Потери давления в местных сопротивлениях участка:

; (16.17)

где åz - сумма коэффициентов местных сопротивлений на участке.

Общие потери давления на участке воздуховода длиной l при наличии местных сопротивлений

. (16.18)

Лекция № 17 Аэродинамический расчет систем вентиляции

План

Дата добавления: 2014-04-10; просмотров: 586; Нарушение авторских прав

Мы поможем в написании ваших работ!