
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ММ-4. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ ЗАДАЧ. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ
3.1. Что такое линейная оболочка системы элементов 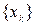 ?
?
А.Сумма их норм.
Б.Сумма расстояний между ними.
В. Выражение 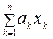 , где
, где 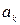 - числа;
- числа;
Г. Множество всехлинейных комбинаций каждых 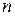 элементов, где
элементов, где 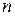 -любое конечное количество этих элементов.
-любое конечное количество этих элементов.
3.2. Что такое линейная независимость элементов конечной системы 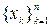 ?
?
А. Невозможность указать такой набор коэффициентов 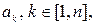 одновременно не равных нулю, чтобы линейная комбинация указанных элементов с этими коэффициентами равнялась нулю.
одновременно не равных нулю, чтобы линейная комбинация указанных элементов с этими коэффициентами равнялась нулю.
Б. Их принадлежность к разным пространствам.
В. Возможность указать такой набор коэффициентов 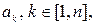 одновременно не равных нулю, чтобы линейная комбинация указанных элементов с этими коэффициентами равнялась нулю.
одновременно не равных нулю, чтобы линейная комбинация указанных элементов с этими коэффициентами равнялась нулю.
Г. Ортогональность элементов системы.
3.3. Что называется подпространством нормированного пространства?
А. Линейная оболочка любой системы элементов этого пространства.
Б. Множество всехлинейных комбинаций каждых 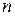 элементов, где
элементов, где 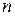 -любое конечное количество этих элементов.
-любое конечное количество этих элементов.
В. Всякое его замкнутое линейное подмножество.
Г. Множество элементов с одинаковой нормой.
3.4. Что называется размерностью пространства?
А. Число 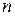 такое, что в пространстве имеется конечное число
такое, что в пространстве имеется конечное число 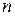 линейно независимых элементов, а любые
линейно независимых элементов, а любые 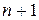 его элементов линейно зависимы. Если в пространстве (или его подпространстве) можно указать произвольное сколь угодно большое (конечное) количество линейно независимых элементов, то оно бесконечномерно.
его элементов линейно зависимы. Если в пространстве (или его подпространстве) можно указать произвольное сколь угодно большое (конечное) количество линейно независимых элементов, то оно бесконечномерно.
Б. Число элементов пространства.
В. Наибольшее расстояние между его элементами.
Г. Наибольшая норма его элемента.
3.5. Что такое базис конечномерного пространства?
А. Любая система его элементов.
Б. Система элементов, количество которых равно размерности пространства.
В. Система ортогональных элементов этого пространства.
Г. Любая система 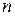 линейно независимых элементов этого пространства, где
линейно независимых элементов этого пространства, где 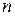 - размерность пространства.
- размерность пространства.
3.6. Что такое базис бесконечномерного пространства?
А. Любая бесконечная система его элементов.
Б. Система ортогональных элементов этого пространства.
В. Такое счётное множество элементов 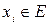 , которое каждый элемент
, которое каждый элемент 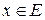 позволяет представить в виде
позволяет представить в виде 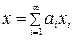 , причём это представление единственнои должно пониматься по аналогии с тем, как понимается сумма ряда.
, причём это представление единственнои должно пониматься по аналогии с тем, как понимается сумма ряда.
Г. Множество элементов с одинаковой нормой.
3.7. Что такое ортогональная система элементов, полная в данном евклидовом пространстве?
А. Любая система ортогональных элементов этого пространства.
Б. Ортогональная система элементов 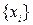
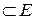 , где
, где 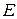 - евклидово пространство, называется полной в
- евклидово пространство, называется полной в 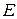 , если в
, если в 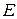 нет элемента
нет элемента 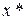 , ортогонального всем элементам системы.
, ортогонального всем элементам системы.
В. Система элементов, ортогональных ко всем элементам данного пространства.
Г. Ортогональная система, все элементы которой имеют единичную норму.
3.8. Что называется энергетическим пространством оператора 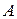 ?
?
А. Полное метрическое пространство, в котором задан этот оператор.
Б. Полное нормированное пространство, в котором задан этот оператор.
В. Замыкание  области определения этого оператора
области определения этого оператора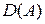 с введенным в него скалярным произведением в виде энергетического произведения и нормой в виде энергетической нормы.
с введенным в него скалярным произведением в виде энергетического произведения и нормой в виде энергетической нормы.
Г. Область определения оператора .
Ответы на тест-самоконтроль3.5 (адрес файла Блок 3 -----)
3.1. «Г» - Множество всех линейных комбинаций каждых 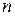 .элементов этой системы
.элементов этой системы
3.2. «А» - Невозможность указать такой набор коэффициентов 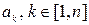 , одновременно не равных нулю, чтобы линейная комбинация указанных элементов с этими коэффициентами равнялась нулю.
, одновременно не равных нулю, чтобы линейная комбинация указанных элементов с этими коэффициентами равнялась нулю.
3.3. «В» - Всякое его замкнутое линейное подмножество.
3.4. «А» - Число 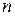 такое, что в пространстве имеется конечное число
такое, что в пространстве имеется конечное число 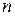 линейно независимых элементов, а любые
линейно независимых элементов, а любые 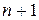 его элемент линейно зависимы. Если в пространстве можно указать произвольное сколь угодно большое конечное количество линейнонезависимых элементов, то оно бесконечномерно.
его элемент линейно зависимы. Если в пространстве можно указать произвольное сколь угодно большое конечное количество линейнонезависимых элементов, то оно бесконечномерно.
3.5. «Г» - любая система 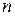 линейно независимых элементов этого пространства, где
линейно независимых элементов этого пространства, где 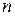 - размерность пространства.
- размерность пространства.
3.6. «В» - Такое счётное множество элементов 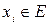 , которое каждый элемент в
, которое каждый элемент в 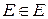 позволяет представить в виде
позволяет представить в виде 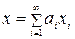 , причём это представление единственно и должно пониматься по аналогии тем, как понимается сумма ряда.
, причём это представление единственно и должно пониматься по аналогии тем, как понимается сумма ряда.
3.7. «Б» - Ортогональная система элементов 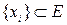 , где
, где 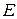 - евклидово пространство, если в
- евклидово пространство, если в 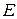 нет элемента, ортогонального всем элементам системы.
нет элемента, ортогонального всем элементам системы.
3.8. «В» - Замыкание области определения этого оператора с введенным в него скалярным произведением в виде энергетического произведения и нормой в виде энергетической нормы.
.

.

 |
ММ-4. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ ЗАДАЧ. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ.
ММ-4. Ключевые слова и понятия
4.1. Линеаризация нелинейной задачи
4.2. Неподвижная точка оператора
4.3. Область сходимости
4.4. Притягивающая точка
4.5. Отталкивающая точка
4.6. Оператор сжатия
4.7. Метод простых итераций для операторного уравнения 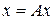
| <== предыдущая страница | | | следующая страница ==> |
| Тест - контроль для самопроверки | | | Входная информация для самопроверки. Для изучения данной темы Вам необходимо восстановить в памяти |
Дата добавления: 2014-04-15; просмотров: 342; Нарушение авторских прав

Мы поможем в написании ваших работ!