
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Входная информация для самопроверки. Для изучения данной темы Вам необходимо восстановить в памяти
Для изучения данной темы Вам необходимо восстановить в памяти:
- из курса прикладной математики - понятия линейной алгебры, числовой последовательности, функциональной последовательности, предела;
-из настоящего спецкурса - понятия: пространства, метрического пространства; расстояния; фундаментальной последовательности; полноты пространства; оператора, линейного оператора.
4.2. Содержание темы
 4.2.1. Структурно – логическая схема содержания темы
4.2.1. Структурно – логическая схема содержания темы
 | |||
 | |||

Тематическое содержание
Как упоминалось в лекции ММ-1, при значительных абсолютных и относительных деформациях (или напряжениях) проявляются нелинейности различной природы – физическая нелинейность, геометрическая нелинейность и нелинейность уравнений равновесия; кроме того, в ряде случаев независимо от уровня деформаций имеет место ещё один, достаточно специфический, вид нелинейности – конструктивная нелинейность. В результате математическая модель деформирования конструкции (системы конструкций) становится нелинейной, что предопределяет необходимость применения специальных методов анализа таких моделей (решения соответствующих нелинейных уравнений или систем таких уравнений). Эти методы, как правило, предусматривают совместное выполнение двух приёмов: сведение исходной нелинейной задачи к последовательности линейных задач и дискретизацию континуальной задачи.
Для усвоения этих методов вначале необходимо ознакомиться с распространёнными стандартными методами аппроксимации и линеаризации, реализуемыми раздельно, независимо друг от друга. При этом для нас представляет интерес только линеаризация, осуществляемая с применением итераций, или последовательных приближений. Идея любого итерационного метода заключается в следующем.
1. В области  некоторого пространства
некоторого пространства 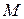 задано уравнение
задано уравнение
 , (4.1)
, (4.1)
где  :
:  - оператор (в общем случае – нелинейный);
- оператор (в общем случае – нелинейный);  - искомый элемент;
- искомый элемент; 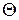 - нулевой элемент.
- нулевой элемент.
Оператор  зависит от своего аргумента
зависит от своего аргумента  :
:  ; например, коэффициенты системы канонических уравнений зависят от усилий (в методе сил) или от деформаций (в методе перемещений), Мы будем этот факт отражать записью воздействия такого оператора на элемент в виде
; например, коэффициенты системы канонических уравнений зависят от усилий (в методе сил) или от деформаций (в методе перемещений), Мы будем этот факт отражать записью воздействия такого оператора на элемент в виде 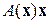 ; всё уравнение (4.1) тогда приобретёт вид
; всё уравнение (4.1) тогда приобретёт вид
 . (4.2)
. (4.2)
Пространство 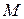 должно предоставлять возможность определения «близости» двух своих элементов – приближенного и точного решений или двух приближённых решений. Из известных нам пространств такую возможность предоставляет метрическое и нормированное пространства (известны другие типы пространств, позволяющие оценить «близость» своих элементов, но нам они не понадобятся).
должно предоставлять возможность определения «близости» двух своих элементов – приближенного и точного решений или двух приближённых решений. Из известных нам пространств такую возможность предоставляет метрическое и нормированное пространства (известны другие типы пространств, позволяющие оценить «близость» своих элементов, но нам они не понадобятся).
Далее следует убедиться, что в этой области уравнение имеет единственный корень, либо разбить область  на подобласти с одним корнем в каждой.
на подобласти с одним корнем в каждой.
2. В каждой подобласти некоторого пространства, в которой разыскивается приближённое решение, выбирается «нулевое приближение» - первый элемент последовательности решений. Это достаточно трудная задача, так как он должен быть достаточно близок к точному решению, которое неизвестно. Обычно (но не всегда!) существует некоторая область, включающая точное решение, из любой точки которой может стартовать вычислительный процесс, порождающий сходящуюся к точному решению последовательность приближённых решений.
Эта область называется областью сходимости данного точного решения.
3. Организуется вычислительный процесс, порождающий последовательность линейных задач и соответствующую последовательность приближённых решений
 , (4.2)
, (4.2)
причём на первом шаге 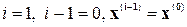 .
.
Обозначение 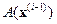 означает, что все параметры оператора
означает, что все параметры оператора 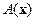 вычисляются при
вычисляются при  то - есть, при фиксированных значениях, полученных на предыдущей итерации.
то - есть, при фиксированных значениях, полученных на предыдущей итерации.
Следовательно, эти задачи линейны, так как 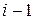 задано и оператор
задано и оператор 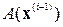 задан и не зависит от
задан и не зависит от  .
.
Все вычисления при фиксированном значении 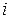 , а также само решение уравнения (4.2), называются
, а также само решение уравнения (4.2), называются 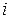 - ой итерацией.
- ой итерацией.
В редких случаях удаётся на каждой итерации найти в замкнутом виде оператор, обратный оператору 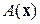 (оператор
(оператор  ), поэтому приходится решать линейную задачу - линейное алгебраическое уравнение или конечную систему линейных алгебраических уравнений, краевую задачу для линейного дифференциального уравнения (обыкновенных или в частных производных) или системы таких уравнений и т.д.
), поэтому приходится решать линейную задачу - линейное алгебраическое уравнение или конечную систему линейных алгебраических уравнений, краевую задачу для линейного дифференциального уравнения (обыкновенных или в частных производных) или системы таких уравнений и т.д.
На каждой итерации проверяется выполнение условия выхода из итерационного цикла– некоторая оценка погрешности(см. лекцию ММ-1) не должна превышать определённую заранее допустимую величину.
Обычно такая оценка погрешности выражается через расстояние между двумя последовательными итерациями (для нас это понятие совпадает с понятием нормы их разности), которое легко определяется в процессе счёта.
Как указывалось в лекции ММ-1, такое сведение нелинейной задачи к последовательности линейных задач (и их решений) называется линеаризацией.
Алгоритм такого счёта иногда называется итерационной схемой. Может быть предложено множество различных итерационных схем, причём каждая из них имеет свою область применения и не может быть применена вне пределов этой области.
Такая область применения устанавливается заранее (обычно, математиками – специалистами в конкретной области вычислительной математики) и формулируются в виде условий (обычно неравенств), накладываемых на функции, записанные в правой части уравнений, на область, в которой разыскивается решение и т.д.

Настоящая лекция посвящена простейшему методу линеаризации – методу простых итераций.
Этот метод предназначен непосредственно для решения нелинейных задач разнообразной природы, однако операторное представление этих уравнений должно иметь специальный вид
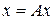 , (4.3)
, (4.3)
где  - искомый элемент (число, вектор, функция, вектор-функция), принадлежащий некоторому пространству
- искомый элемент (число, вектор, функция, вектор-функция), принадлежащий некоторому пространству  ;
;  - оператор. Следует, однако, отметить, что почти всегда система уравнений, которую необходимо решить, может быть приведена различными способами к виду (4.3), и проблема состоит скорее в выборе такого способа.
- оператор. Следует, однако, отметить, что почти всегда система уравнений, которую необходимо решить, может быть приведена различными способами к виду (4.3), и проблема состоит скорее в выборе такого способа.
Идея метода чрезвычайно проста. Выбирается начальное приближение  и критерий выход из цикла(обеспечивающий достаточную точность приближения)
и критерий выход из цикла(обеспечивающий достаточную точность приближения) 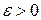 , после чегоначинается выполнение итераций
, после чегоначинается выполнение итераций  где
где  - процедура проверки возможности выхода из цикла
- процедура проверки возможности выхода из цикла  если
если 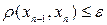 , то можно прекратить итерации и принять
, то можно прекратить итерации и принять 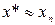 . Напоминаем: так как точное решение
. Напоминаем: так как точное решение  неизвестно, точная мера погрешности решения
неизвестно, точная мера погрешности решения  , где
, где 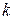 - номер последней выполненной итерации, не может быть определена. Определяется лишь оценка величины
- номер последней выполненной итерации, не может быть определена. Определяется лишь оценка величины 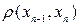 , по которой, как мы установим далее, можно при выполнении определённых условий определить оценку меры погрешности. Таким образом, в результате применения этого метода мы получаем последовательность приближённых решений
, по которой, как мы установим далее, можно при выполнении определённых условий определить оценку меры погрешности. Таким образом, в результате применения этого метода мы получаем последовательность приближённых решений 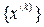 ; необходимо ответить на вопросы: а) сходится ли эта последовательность? б) если сходится, то к точному решению или нет? в) когда прекратить выполнение итераций?
; необходимо ответить на вопросы: а) сходится ли эта последовательность? б) если сходится, то к точному решению или нет? в) когда прекратить выполнение итераций?
Для метода простых итераций установлены достаточно общие условия, обеспечивающие сходимость последовательности решений линейных задач (иначе – условия сходимости итерационного процесса, или условия сходимости метода), порождаемых этим методом, к точному решению задачи (7.1). Благодаря отмеченной выше возможности сведения разнообразных задач к виду (7.1) возможен анализ условий сходимости различных методов линеаризации на базе отмеченных выше общих условий сходимости метода простых итераций.
Вначале введём некоторые определения.
Пусть мы нашли решение уравнения (4.3), то - есть, такой элемент  , который превращает (4.3) в тождество
, который превращает (4.3) в тождество 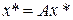 . Тогда
. Тогда  называется неподвижной точкой оператора
называется неподвижной точкой оператора  , действующего из
, действующего из  в
в  (
( ).
).
|

Для того, чтобы метод простых итераций сходился, необходимо выполнение определённых условий. В общем случае это условие достаточно неопределённо:  должно быть выбрано достаточно «близко» к
должно быть выбрано достаточно «близко» к  (в то время, как
(в то время, как  неизвестно!), и представляет интерес: каково множество таких элементов, которые можно выбирать в качестве начального приближения, то - есть, таких точек, для которых последовательность решений
неизвестно!), и представляет интерес: каково множество таких элементов, которые можно выбирать в качестве начального приближения, то - есть, таких точек, для которых последовательность решений  сходится к
сходится к  ?
?


|

Условия сходимости метода простых итераций, установленные Банахом, содержат требования к оператору задачи  и к пространству
и к пространству  , которому принадлежат элементы
, которому принадлежат элементы  и последовательность приближённых решений
и последовательность приближённых решений 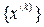 . А именно, оператор
. А именно, оператор  должен быть оператором сжатия.
должен быть оператором сжатия.
|
к оператору задачи 
Иногда  называют константой Липшица оператора
называют константой Липшица оператора  , хотя чаще применяют этот термин в частном случае, когда в роли оператора выступает числовая функция. Условие
, хотя чаще применяют этот термин в частном случае, когда в роли оператора выступает числовая функция. Условие 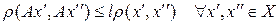 называют в этом случае условием Липшица.
называют в этом случае условием Липшица.
Теперь мы можем сформулировать теорему Банаха о неподвижной точке в метрическом пространстве
Теорема Банаха. Пусть  - полное метрическое пространство и оператор
- полное метрическое пространство и оператор 
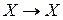 является оператором сжатия. Тогда этот оператор имеет единственную неподвижную точку
является оператором сжатия. Тогда этот оператор имеет единственную неподвижную точку  (решение уравнения
(решение уравнения 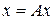 ), которая может быть найдена методом простых итераций. Начальный элемент
), которая может быть найдена методом простых итераций. Начальный элемент 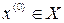 может быть выбран в нём произвольно.
может быть выбран в нём произвольно.
Лемма. . . (4.4)
. . (4.4)
Доказательство леммы. Умножим левую часть (4.4) на 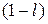
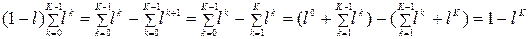
(здесь в первых скобках записана первая сумма, во вторых скобках – вторая). Разделив теперь первое и последнее выражения на 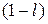 , мы получим равенство, которое и требовалось доказать.
, мы получим равенство, которое и требовалось доказать.
Доказательство теоремы. По условию теоремы, заданное пространство – полное. Следовательно, для того, чтобы установить наличие предела, достаточно доказать, что последовательность  фундаментальна. Для этого исследуем поведение
фундаментальна. Для этого исследуем поведение  при
при  . Согласно аксиоме треугольника
. Согласно аксиоме треугольника
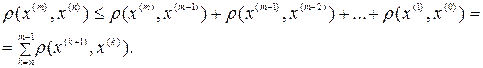 (4.5)
(4.5)
Дадим оценку расстояния между двумя последовательными элементами 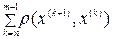 :
:
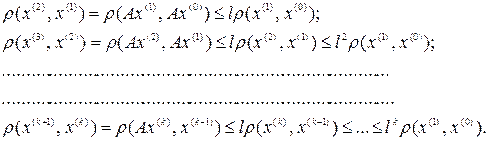
Итак,
 (4.6)
(4.6)
Подставляя (7.4) в (7.3), получим
 (4.7)
(4.7)
Используя доказанное в лемме равенство (4.4) для вычисления 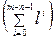 , приведём правую часть (4.7) к виду
, приведём правую часть (4.7) к виду
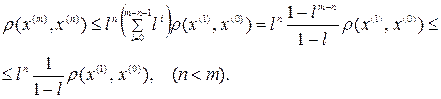 (4.8)
(4.8)
Теперь мы можем проверить, является ли при выполнении условий теоремы последовательность 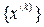 сходящейся (здесь учтено, что
сходящейся (здесь учтено, что 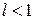 и
и 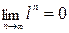 ):
):
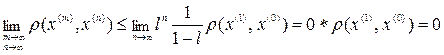 . (4.9)
. (4.9)
Таким образом, последовательность приближённых решений 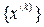 фундаментальна и, вследствие условия теоремы о полноте пространства, в котором действует оператор, она в этом пространстве имеет предел.
фундаментальна и, вследствие условия теоремы о полноте пространства, в котором действует оператор, она в этом пространстве имеет предел.
Таким образом, мы установили существование неподвижной точки и возможность её определения методом простых итераций.
Единственность такой точки можно установить следующим образом. Пусть оператор сжатия  , где
, где  - полное метрическое пространство, имеет две неподвижные точки:
- полное метрическое пространство, имеет две неподвижные точки: 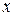 и
и 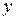 , то – есть,
, то – есть,  . Тогда, по определению оператора сжатия,
. Тогда, по определению оператора сжатия, 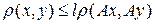 . Подставляя сюда
. Подставляя сюда 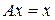 и
и 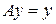 , получим
, получим
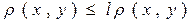 .
.
При 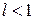 это неравенство может выполняться только при
это неравенство может выполняться только при  , то – есть, при
, то – есть, при  .
.
Добавления.
1.  может быть замкнутым подпространством полного метрического пространства.
может быть замкнутым подпространством полного метрического пространства.
2. Оценка погрешности 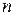 - го приближения может быть получена по формуле
- го приближения может быть получена по формуле
 , (4.10)
, (4.10)
где  - константа Липшица оператора
- константа Липшица оператора  .
.
3. Из (4.10) легко получить количество итераций, гарантирующее, что погрешность не будет превосходить заданную величину  (с учётом
(с учётом 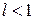 )
)
 . (4.11)
. (4.11)
4. В ряде случаев может быть более эффективной проверка такого признака, который легко прослеживать на каждой итерации. Такой признак может быть установлен на основании (4.6)
 (4.12)
(4.12)
и оценки (4.10) в сочетании с требованием 
 . (4.13)
. (4.13)
Из (4.13) непосредственно следует
 . (4.14)
. (4.14)
Подставляя (4.14) в (4.12), получим искомое условие выхода из цикла, использующее расстояние между двумя последовательными приближениями, контроль которого во время вычислений осуществляется наиболее легко
 . (4.15)
. (4.15)
Анализ приведенных условий выхода из цикла показывает, что чем меньше  и
и  (то – есть, чем ближе нулевое приближение к точному), тем меньшее число итераций требуется для достижения заданной точности или тем большая точность может быть достигнута при заданном числе итераций.
(то – есть, чем ближе нулевое приближение к точному), тем меньшее число итераций требуется для достижения заданной точности или тем большая точность может быть достигнута при заданном числе итераций.
 | |||
|
Если необходимо решить нелинейное уравнение, то – есть, уравнение (4.3) имеет вид
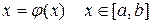 , (4.16)
, (4.16)
где 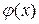 - нелинейная функция, непрерывная на
- нелинейная функция, непрерывная на 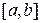 и дифференцируемая на
и дифференцируемая на 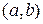 , то определение константы Липшица осуществляется следующим образом. Разобьём отрезок
, то определение константы Липшица осуществляется следующим образом. Разобьём отрезок 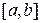 возрастающей последовательностью
возрастающей последовательностью 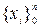 ,
,  на подобласти
на подобласти 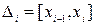 и запишем для каждой из них теорему Лагранжа
и запишем для каждой из них теорему Лагранжа
 , (4.17)
, (4.17)
где  .
.
Тогда для каждого  при любой его длине
при любой его длине  константа Липшица в его пределах
константа Липшица в его пределах
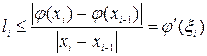 . (4.18)
. (4.18)
При  его концы сближаются и
его концы сближаются и 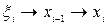 , откуда в пределе
, откуда в пределе
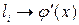 , (4.19)
, (4.19)
где 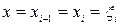 .
.
Для всего отрезка 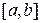
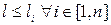 , поэтому в качестве константы Липшица можно принять
, поэтому в качестве константы Липшица можно принять
 . (4.20)
. (4.20)
Тогда условие выхода из цикла (4.15) приводится к виду
 . (4.21)
. (4.21)
В случае решения одного нелинейного уравнения возможны два варианта модификации теоремы Банаха.
Вариант 1. Пусть на  нелинейная функция
нелинейная функция 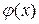 удовлетворяет условию Липшица с
удовлетворяет условию Липшица с 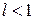 и
и 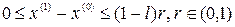 . В этом случае уравнение (4.16) имеет единственное решение
. В этом случае уравнение (4.16) имеет единственное решение 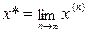 и
и 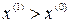 .
.
В этом варианте итерационный процесс стартует с левого конца области поиска решения.
Вариант 2 отличается: а) областью поиска (она расположена слева от начального приближения: 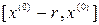 ) и б) одним из условий (теперь
) и б) одним из условий (теперь 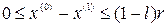 ). В этом случае процесс стартует с правого конца области поиска.
). В этом случае процесс стартует с правого конца области поиска.
В случае, если решается система 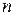 нелинейных уравнений с
нелинейных уравнений с 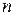 неизвестными,
неизвестными,
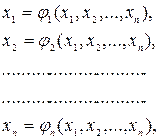 (4.22)
(4.22)
или в компактной векторно – матричной записи
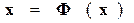 , (4.23)
, (4.23)
где 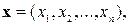
 , определение константы Липшица основывается на тех же соображениях. Однако, она должна теперь отражать свойства всей совокупности функций
, определение константы Липшица основывается на тех же соображениях. Однако, она должна теперь отражать свойства всей совокупности функций 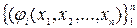 , поэтому нам следует рассматривать все
, поэтому нам следует рассматривать все 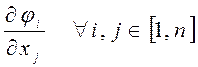 .
.
Исходя из этого, введём в рассмотрение матрицу Якобиуказанной выше совокупности функций 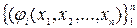 :
:
 . (4.24)
. (4.24)
Другое обозначение матрицы Якоби
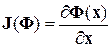 . (4.25)
. (4.25)

По
Теперь по аналогии со случаем одного уравнения заменим производные (то - есть, тоже функции) максимумами их модулей
 . (4.26)
. (4.26)
Таким образом, мы вместо одного числа, которому можно было бы приписать роль константы Липшица, имеем 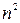 чисел.
чисел.
Для преодоления этой трудности нам потребуется ввести понятие нормы матрицы. Здесь для нас важна роль матрицы как оператора  в выражении для дифференциала вектор – функции
в выражении для дифференциала вектор – функции 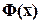
 . (4.27)
. (4.27)
Поэтому дадим вначале более общее понятие нормы линейного оператора.
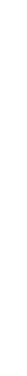 |

 ример расчёта.ана система уравнений
ример расчёта.ана система уравнений
|

Поскольку в определении нормы оператора участвует понятие нормы элемента  , способ определения нормы оператора зависит от определения нормы элемента. В соответствии с этим норма
, способ определения нормы оператора зависит от определения нормы элемента. В соответствии с этим норма  матрицы
матрицы  определяется следующим образом
определяется следующим образом
если норма вектора  принимается равной
принимается равной 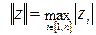 , то
, то
 , (4.28)
, (4.28)
если норма вектора  принимается равной
принимается равной  , то
, то
можно применять два варианта определения нормы матрицы
1) норма Шмидта (иногда называется евклидовой, а также сферической)
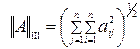 ; (4.29)
; (4.29)
2) спектральная норма – определяется как наибольшее собственное число матрицы 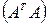
Теперь мы можем определить константу Липшица для матрицы - оператора 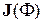 :
:
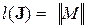 . (4.30)
. (4.30)
Из определения расстояния, нормы вектора и нормы оператора, а также приведенных способов определения нормы матрицы легко усмотреть, что (4.30) действительно задаёт константу Липшица оператора 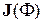 :
:
Решение системы (4.22) методом простых итераций заключается в многократном повторении вычислений по формуле
 , (4.31)
, (4.31)
где 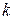 - номер итерации.
- номер итерации.
При решении системы (4.22) возможна модификация метода, сходная с методом Зейделя решения систем линейных алгебраических уравнений
 . (4.32)
. (4.32)
Смысл этой модификации состоит в том, что на каждой 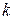 -ой итерации для вычисления значения функции
-ой итерации для вычисления значения функции 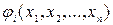 используются уже определённые на этой итерации значения неизвестных
используются уже определённые на этой итерации значения неизвестных  с меньшими нижними индексами (
с меньшими нижними индексами (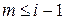 ).
).
Пример.
Требуется найти решение системы
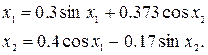
с допустимой погрешностью  .
.
1. Локализуем корень системы. Из первого уравнения и неравенств  следует, что
следует, что 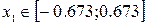 . В этом диапазоне
. В этом диапазоне 
 , и второе уравнение даёт
, и второе уравнение даёт 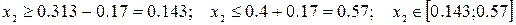 .
.
2. Определим оценку константы Липшица, установим возможность применения метода и определим условие прекращения вычислений:
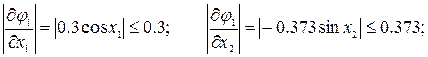

Следовательно,  .
.
Итак, применение метода простых итераций возможно.
Условие выхода из цикла 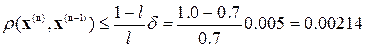
3. Назначим начальное приближение (трудоёмкие прикидки отвлекли бы нас от основной идеи лекции, поэтому опущены): 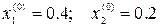 .
.
4. Организуем модифицированный итерационный цикл
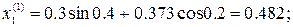
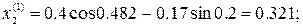
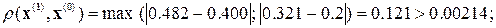
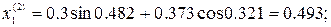

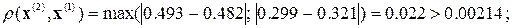

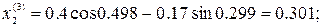
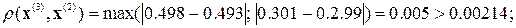

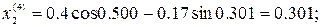
 .
.
Следовательно, решение 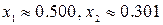 с погрешностью, не превышающей допустимую величину, приближает точное решение.
с погрешностью, не превышающей допустимую величину, приближает точное решение.
4.3. Критерии усвоения
После изучения содержания данной темы Вы должны:
·
| |
как решаются методом простых итераций нелинейные уравнения и системы нелинейных уравнений;
каким условиям должны удовлетворять уравнения для того, чтобы их можно было решать методомпростых итераций;
как контролируется погрешность очередной итерации;
· понимать
роль каждого условия применения метода;
смысл алгоритма решения на каждой итерации;
· Уметь
применять метод простых итераций для решения нелинейных уравнений и их систем..
4.4. Выход темы в другие темы и дисциплины
Данная тема имеет выход в дипломные, магистерские и диссертационные работы.
4.5. Тест - контроль для самопроверки
4.1. Что называется линеаризацией нелинейной задачи?
А. Следующая последовательность процедур:
1. Проверка выполнения условий применения данной итерационной схемы.
2. Разделение корней (выделение подобластей, включающих единственный корень) и выбор нулевых приближений для каждой подобласти..
3. Выполнение итераций, включающих
- формулирование линейной задачи 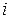 - ой итерации;
- ой итерации;
- решение этой задачи с использованием результатов предыдущей итерации (предыдущих итераций);
- проверка условий выхода из итерационного цикла;
- при выполнении указанных условий – выход из цикла.
Б. Формулирование линейной задачи 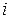 - ой итерации.
- ой итерации.
В. Формулирование и решение линейной задачи 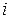 - ой итерации с использованием результатов предыдущей итерации (предыдущих итераций).
- ой итерации с использованием результатов предыдущей итерации (предыдущих итераций).
Г. Преобразование нелинейной задачи в линейную задачу.
4.2. Что называется неподвижной точкой оператора?
А. Наименьшее из таких чисел 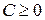 , для которых выполняется условие
, для которых выполняется условие
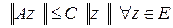 ,
,
где 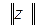 и
и 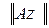 - нормы элемента
- нормы элемента 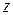 и его образа
и его образа  .
.
Б. Элемент 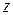 , удовлетворяющий условию
, удовлетворяющий условию  , где
, где  - заданный оператор,
- заданный оператор, 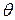 - нулевой элемент.
- нулевой элемент.
В. Элемент  , удовлетворяющий условию
, удовлетворяющий условию 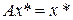 .
.
Г. Элемент 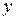 .такой, что
.такой, что  , где
, где  - заданный оператор.
- заданный оператор.
4.3. Что такое область сходимости неподвижной точки оператора  ?
?
А. Область  , если для каждой точки
, если для каждой точки  существует элемент
существует элемент  .
.
Б. Область  , если для каждой точки
, если для каждой точки  можно указать такой элемент
можно указать такой элемент 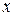 , что
, что  .
.
В. Множество всех элементов 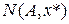 такое, что для любого
такое, что для любого 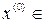
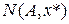 последовательность
последовательность  принадлежит ей.
принадлежит ей.
Г. Множество всех элементов 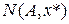 такое, что для любого
такое, что для любого 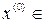
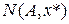 последовательность
последовательность  сходится к
сходится к  .
.
4.4. Что называется оператором сжатия?
А. Оператор  , удовлетворяющий условию
, удовлетворяющий условию  , где
, где  - нулевой элемент.
- нулевой элемент.
Б. Оператор  , удовлетворяющий условию
, удовлетворяющий условию 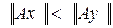 , если
, если  .
.
В. Оператор  , для которого можно указать постоянную
, для которого можно указать постоянную  такую, что
такую, что 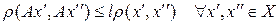 .
.
Г. Оператор  , для которого можно указать постоянную
, для которого можно указать постоянную  такую, что
такую, что 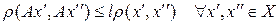 .
.
4.5. Что называется методом простых итераций?
А. Следующая последовательность вычислительных процедур.
1. Проверка возможности использования метода.
2. Выбор начальной точки.
3. Последовательное выполнение итераций, причём любая 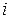 - ая итерация выполняется по формуле
- ая итерация выполняется по формуле  .
.
4. Условия выхода из цикла могут иметь следующий вид:
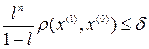 ,
,
 ,
,
 .
.
Б. Следующая последовательность вычислительных процедур:
1. Проверка возможности использования метода.
2. Выбор начальной точки.
3. Последовательное выполнение итераций, причём любая 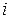 - ая итерация выполняется по формуле
- ая итерация выполняется по формуле  .
.
4. Условия выхода из цикла могут иметь следующий вид:
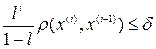 ,
,
 ,
,
 .
.
В. Следующая последовательность вычислительных процедур:
1. Проверка возможности использования метода.
2. Выбор начальной точки.
3. Последовательное выполнение итераций, причём любая 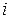 - ая итерация выполняется по формуле
- ая итерация выполняется по формуле 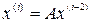 .
.
4. Условия выхода из цикла могут иметь следующий вид:
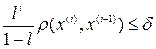 ,
,
 ,
,
 .
.
Г. Следующая последовательность вычислительных процедур:
1. Проверка возможности использования метода.
2. Выбор начальной точки.
3. Последовательное выполнение итераций, причём любая 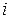 - ая итерация выполняется по формуле
- ая итерация выполняется по формуле  .
.
4. Условия выхода из цикла могут иметь следующий вид:
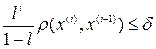 ,
,
 ,
,
 .
.
|



А. Следующая последовательность процедур:
1. Проверка выполнения условий применения данной итерационной схемы.
2. Разделение корней (выделение подобластей, включающих единственный корень) и выбор нулевых приближений для каждой подобласти..
3. Выполнение итераций, включающих
- формулирование линейной задачи 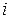 - ой итерации;
- ой итерации;
- решение этой задачи с использованием результатов предыдущей итерации (предыдущих итераций);
- проверка условий выхода из итерационного цикла;
- при выполнении указанных условий – выход из цикла

| <== предыдущая страница | | | следующая страница ==> |
| ММ-4. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ ЗАДАЧ. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ | | | ММ-6. ДИСКРЕТИЗАЦИЯ ФУНКЦИОНАЛЬНОГО ПРОСТРАНСТВА |
Дата добавления: 2014-04-15; просмотров: 404; Нарушение авторских прав

Мы поможем в написании ваших работ!
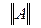 линейного оператора
линейного оператора  , где
, где  - нормированное пространство, называется наименьшее из таких чисел
- нормированное пространство, называется наименьшее из таких чисел  .
.
 Вернитесь к тексту
Вернитесь к тексту