ММ-7. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ. РЕШЕНИЕ НЕЛИНЕЙНЫХ ЗАДАЧ СТРОИТЕЛЬНОЙ МЕХАНИКИ

2. Необходимость выбора полной (то-есть, бесконечной) координатной системы, с использованием при каждом последовательном расчёте первых 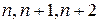и т.д. функций.Как указыавлось выше, в общем случае произвольную функцию 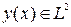можно описать при помощи координатной системы, полной в этом пространстве; так как оно бесконечномерно, то и указанная система должна быть бесконечной. Однако, расчёт можно выполнять только с конечной её подсистемой. Поэтому в общем случае следует выбирать бесконечную систему, полную в пространстве, которому принадлежит точное решение. В качестве таких систем можно указать систему степенных функций в 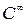, тригонометрическую систему 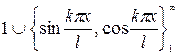или системы различных ортогональных многочленов, определяемых областью 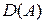, - в .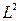

В то же время эта система должна быть минимальной,то-есть. Такой. стобы вычёркивание любой её функции изменяло размерность натянутого на неё подпространства, сужало возможность описания произвольной функции линейной комбинацией координатных функций – среди функций системы не должно быть «лишних», «бесполезных», линейно зависящих от других функций системы.

В общем случае необходимо выбирать полную минимальную систему (бесконечную) систему и, при каждом расчёте. – её конечную пдсистему с возрастющим количеством функций.

.

6.3. Критерии усвоения

После изучения содержания данной темы Вы должны:

·

содержание понятий «линейная аппроксимация», «координатная функция», «координатная система», проекция точного решения в подпространство»;

в чём заключается соответствие «краевая задача – вариационная задача»;

каким условиям должен отвечать оператор задачи, чтобы это соответствие имело место;

каким условиям должна удовлетворять координатная система;

к какой задаче сводится краевая задача на последнем шаге метода Ритца;

как определить элементы матрицы Ритца и сбодный член получаемой этим методом системы уравнений;

каким условиям необходимо подчинить невязку, чтобы получить элемент наилучшего приближения методом Бубнова-Галёркина;

каковы преимущества метода Бубнова-Галёркина;

сколько разнеобходимо выполнять расчёт прямыми методами.

· Понимать

смысл понятия «проекция в подпространство»;

связь этого понятия с понятием «приближённое решение»;

смысл ограничений, налагаемых на оператор задачи;

смысл требований к координатной системе;

зачем ищется решение вариационной задачи в методе Ритца;

смысл требований к невязке при поиске элемента наилучшего приближения в методе Бубнова-Галёркина.

· Уметь

Уметь приводить краевую задачу к системе линейных алгебраических уравнений методом Ритца и методом Бубнова-Галёркина, определять коэффициенты и свободные члены этой системы;

применять каждый из изложенных методов при решении простых задач расчёта балок на упругом основании, сжато-изогнутых элементов

6.4. Выход темы в другие темы и дисциплины

Данная тема имеет выход в дипломные, магистерские и диссертационные работы.

6.5. Тест - контроль для самопроверки

6.1. Что называется элементом наилучшего приближения?

А. Элементом наилучшего приближения элемента 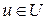в подпространстве 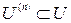называется линейная комбинация координатных функций..

Б. Элементом наилучшего приближения элемента 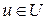в подпространстве 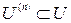называется работа внутренних сил на возможных перемещениях.

В. Элементом наилучшего приближения элемента 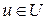в подпространстве 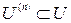называется работа внутренних сил на действительных перемещениях.

Г. Элементом наилучшего приближения элемента 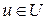в подпространстве 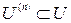называется такой элемент 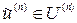, для которого выполняется требование .

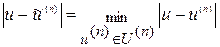6.2. Что называется координатными функциями?

А. Заранее выбранные в 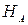(для метода Ритца) и в 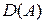(для метода Бубнова-Галёркина) функции, при помощи линейной комбинации которых записывается приближённое решение.

Б. Заранее выбранные в 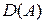(для метода Ритца) и в 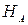(для метода Бубнова-Галёркина) функции, при помощи линейной комбинации которых записывается приближённое решение.

В. Разность между левой и правой частями дифференциального уравнения задачи.

Г. Правая часть дифференциального уравнения задачи.

6.3. Что называется координатной системой?

А. Система коэффициентов линейной аппроксимации решения.

Б. Система коэффициентов линейной аппроксимации свободного члена дифференциального уравнения задачи.

В. Система координатных функций 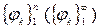, удовлетворяющая определённым требованиям, обеспечивающим сходимость последовательности приближённых решений и повышающих устойчивость процесса счёта.

Г. Система ортов осей координат.

6.4. В чём заключается метод Ритца?

А. В использовании линейной аппроксимации решения.

Б. В следующих действиях

1) формулируется вариационная задача, эквивалентная данной краевой задаче;

2.) выбирается координатная система, отвечающая установленным требованиям;

3) поочерёдно выбираются координатные подсистемы с растущим количеством координатных функций в них и для каждой подсистемы

а) определяются коэффициенты Ритца;

б) определяются свободные члены системы уравнений Ритца;

в) решается система уравнений Ритца;

г) сравнивается норма разности решений с допускаемой величиной (можно сравнивать два последовательных набора коэффициентов, исключая последний коэффициент последующего набора);

д) принимается решение о продолжении счёта или выходе из цикла;

4) формируется линейная комбинация координатных функций с полученными коэффициентами последнего расчёта и вычисляются значения исокмой функции в назаначенных точках её области определения.

В. В использовании линейной апроксимации свободного члена дифференциального уравнения задачи.

Г. В сведении краевой задачи к вариационной.

6.5. В чём заключается метод Бубнова-Галёркина?

А. В использовании линейной аппроксимации решения

Б. В следующем

1) формулируется вариационная задача, эквивалентная данной краевой задаче;

2.) выбирается координатная система, отвечающая установленным требованиям;

3) поочерёдно выбираются координатные подсистемы с растущим количеством координатных функций в них и для каждой подсистемы

а) определяются коэффициенты Ритца;

б) определяются свободные члены системы уравнений Ритца;

в) решается система уравнений Ритца;

г) сравнивается норма разности решений с допускаемой величиной (можно сравнивать два последовательных набора коэффициентов, исключая последний коэффициент последующего набора);

д) принимается решение о продолжении счёта или выходе из цикла;

4) формируется линейная комбинация координатных функций с полученными коэффициентами последнего расчёта и вычисляются значения исокмой функции в назаначенных точках её области определения.

В. В использовании линейной апроксимации свободного члена дифференциального уравнения задачи.

Г. В следующем

1) выбирается координатная система, отвечающая установленным требованиям;

2) поочерёдно выбираются координатные подсистемы с растущим количеством координатных функций в них и для каждой подсистемы

а) записываются условия ортогональности невязки функциям координатной подсистемы;

б) определяются коэффициенты системы линейных алгебраических уравнений метода;

в) определяются свободные члены этой системы;

г) решается эта система уравнений;

д) сравнивается норма разности решений с допускаемой величиной (можно сравнивать два последовательных набора коэффициентов, исключая последний коэффициент последующего набора);

е) принимается решение о продолжении счёта или выходе из цикла;

3) формируется линейная комбинация координатных функций с полученными коэффициентами последнего расчёта;

4) вычисляются значения исокмой функции в назаначенных точках её области определения.

ММ-7. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ. РЕШЕНИЕ НЕЛИНЕЙНЫХ ЗАДАЧ СТРОИТЕЛЬНОЙ МЕХАНИКИ

ММ-7. Ключевые слова и понятия

7.1. Ограниченный носитель.

7.2. Финитные функции.

7.3. Конечный элемент.

7.4. Узел конечного элемента.

7.5. Узел расчётной схемы системы.

7.6. Сетка конечных элементов.

7.7. Сетка узлов системы.

7.8. Конечноэлементная расчётная схема системы.

7.9. Координатные функции МКЭ (функции формы, функции распределения).

7.10. Матрица жёсткости конечного элемента..

7.11. Матрица жёсткости системы.

7.12. Ансамблирование

7.13. Метод переменных параметров упругости.

7.14. Метод фиктивных нагрузок и вынужденных деформаций.

7.15. Шагово-итерационные методы.

Дата добавления: 2014-04-15; просмотров: 601; Нарушение авторских прав

Мы поможем в написании ваших работ!