
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Средняя арифметическая и ее свойства
Средняя арифметическая вычисляется либо как простая, либо как взвешенная величина.
При расчете средней заработной платы по данным таблицы примера 6.1 мы сложили все значения признака и поделили на их количество. Ход наших вычислений запишем в виде формулы средней арифметической простой
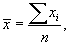
где хi – варианты (отдельные значения признака);
п – число единиц в совокупности.
Пример 6.2. Теперь сгруппируем наши данные из таблицы примера 6.1, т. е. построим дискретный вариационный ряд распределения работающих по уровню заработной платы. Результаты группировки представлены в таблице.
Распределение работников предприятия по уровню заработной платы

Запишем выражение для вычисления среднего уровня заработной платы в более компактной форме:
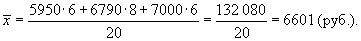
В примере 6.2 была применена формула средней арифметической взвешенной
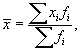
где fi – частоты, показывающие, сколько раз встречается значение признака хi y единиц совокупности.
Расчет средней арифметической взвешенной удобно проводить в таблице, как это показано ниже (табл. 6.1):
Таблица 6.1 – Расчет средней арифметической в дискретном ряду
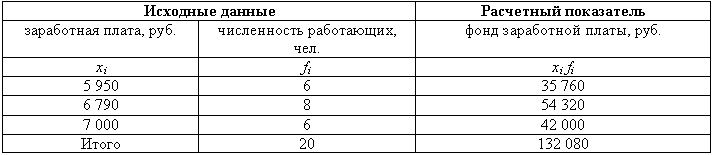
Средняя арифметическая простая используется в тех случаях, когда данные не сгруппированы или сгруппированы, но все частоты равны между собой.
Часто результаты наблюдения представляют в виде интервального ряда распределения (см. таблицу в примере 6.4). Тогда при расчете средней в качестве хi берут середины интервалов. Если первый и последний интервалы открыты (не имеют одной из границ), то их условно «закрывают», принимая за величины данного интервала величину примыкающего интервала, т.е. первый закрывают исходя из величины второго, а последний – по величине предпоследнего.
Пример 6.3.По результатам выборочного обследования одной из групп населения рассчитаем размер среднедушевого денежного дохода.
В приведенной таблице середина первого интервала равна 500. Действительно, величина второго интервала – 1000 (2000 - 1000); тогда нижняя граница первого равна 0 (1000 - 1000), а его середина – 500. Аналогично поступаем с последним интервалом. За его середину принимаем 25 000: величина предпоследнего интервала 10 000 (20 000 - 10 000), тогда его верхняя граница – 30 000 (20 000 + 10 000), а середина, соответственно, - 25 000.
Расчет средней арифметической в интервальном ряду
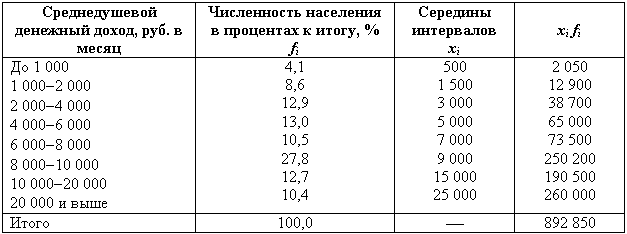
Тогда среднедушевой размер месячного дохода составит
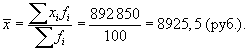
Средняя арифметическая величина обладает рядом математических свойств. Приведем основные из них:
1) если хi = с, где с – постоянная величина, то средняя арифметическая будет равна с;
2) сумма отклонений значений признака от его средней арифметической равна 0, т. е. 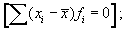
3) если из всех значений признака вычесть постоянную величину с, то средняя арифметическая уменьшится на эту величину с:
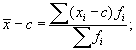
4) от уменьшения или увеличения частот fi каждого значения признака в т раз величина средней арифметической не изменится:
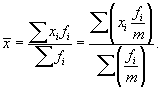
5) если все индивидуальные значения признака уменьшить или увеличить в d раз, то величина средней арифметической также уменьшится или увеличится в d раз:
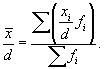
На изложенных свойствах средней арифметической базируется один из методов ее расчета – способ моментов, или метод отсчета от условного нуля, который используется в случае вариационных рядов с равными интервалами. Согласно этому методу среднюю арифметическую взвешенную можно вычислить по следующей формуле:
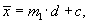
где 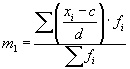 – момент первого порядка.
– момент первого порядка.
За d, как правило, принимают величину интервалов, а за с – значение середины интервала, находящегося в центре ряда (если количество интервалов нечетное), или середину интервала с наибольшей частотой также из центра ряда (при четном количестве интервалов в центре ряда будут находиться два интервала).
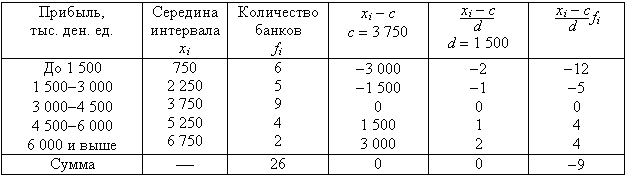
Пример 6.4.Рассчитаем среднюю прибыль по группе банков способом моментов.
Расчет средней арифметической способом моментов
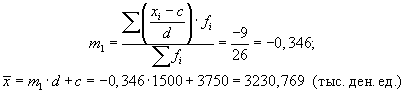
| <== предыдущая страница | | | следующая страница ==> |
| Заработная плата работников | | | Средняя гармоническая |
Дата добавления: 2014-04-24; просмотров: 1567; Нарушение авторских прав

Мы поможем в написании ваших работ!