
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Глава 11. Выборочное наблюдение в статистике
11.1.1. Основные определения и обозначения
Под термином генеральная совокупность понимается изучаемая статистическая совокупность, из которой проводится отбор единиц для непосредственного наблюдения (количество единиц генеральной совокупности обозначается через N).
Отобранная по определенным правилам часть единиц генеральной совокупности образует выборочную совокупность (n – количество единиц выборочной совокупности).
Доля выборочной совокупности в общем объеме генеральной совокупности, выраженная в процентах, называется долей отбора (процентом выборки, процентом отбора):
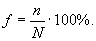
Например, при объеме генеральной совокупности в 200 единиц и выборочной – в 50 единиц говорят о 25%-ной выборке (доля отбора – 25%).
Если исследуется количественный признак, то непосредственная задача выборочного наблюдения – это оценка среднего и суммарного значения признака. Среднее значение признака в генеральной совокупности принято обозначать через 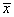 . По данным генеральной совокупности оно может быть определено как
. По данным генеральной совокупности оно может быть определено как
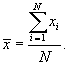
Среднее значение признака в выборочной совокупности обозначается через 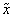 . Оно исчисляется как
. Оно исчисляется как
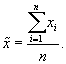
Дисперсия единиц количественного признака определяется следующим образом:
- генеральная дисперсия
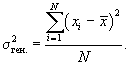
Так как генеральная дисперсия по большей части в ходе исследования остается неизвестной, то условно принимают ее равной дисперсии, рассчитываемой по выборочным данным;
- выборочная дисперсия
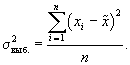
Обозначая численность единиц, обладающих изучаемым признаком, в генеральной совокупности через М, а в выборочной – через т, получим долю единиц, обладающих исследуемым признаком в генеральной совокупности: 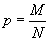 и в выборочной:
и в выборочной: 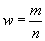 .
.
Дисперсия альтернативного признака рассчитывается следующим образом:
- генеральная дисперсия доли
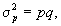
где q – доля единиц, не обладающих исследуемым признаком (q=1-p);
выборочная дисперсия доли
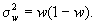
| <== предыдущая страница | | | следующая страница ==> |
| Показатели относительного изменения уровней динамического ряда | | | Способы отбора единиц в выборочную совокупность. Классификация видов выборочного наблюдения |
Дата добавления: 2014-04-24; просмотров: 531; Нарушение авторских прав

Мы поможем в написании ваших работ!