Показатели относительного изменения уровней динамического ряда

Характеристиками относительного изменения уровней ряда динамики являются коэффициенты и темпы роста значений показателя и темпы их прироста.

Коэффициент роста представляет собой соотношение двух уровней динамического ряда, выраженное в виде простого кратного отношения. Он показывает, во сколько раз изменилось значение показателя в одном периоде (моменте) времени по сравнению с другим. Темп роста – это коэффициент роста,выраженный в процентах. Он показывает, сколько процентов составляет значение показателя в данном периоде, если уровень, с которым проводится сравнение, принять за 100%.

Так же, как и абсолютные приросты, коэффициенты и темпы роста могут быть цепными и базисными.

Цепные коэффициент и темп роста измеряют относительное изменение текущего уровня показателя по сравнению с предшествующим ему уровнем:

коэффициент роста:

темп роста:

Базисные коэффициент и темп роста характеризуют относительное изменение текущего уровня показателя по сравнению с базисным (чаще всего с первым) уровнем:

коэффициент роста

темп роста

Цепные и базисные коэффициенты роста имеют между собой следующую связь:

- произведение всех рассчитанных до текущего периода цепных коэффициентов роста дает базисный коэффициент роста текущего периода:

- деление базисного коэффициента роста текущего периода на базисный коэффициент роста предшествующего периода дает цепной коэффициент роста текущего периода

Средние темп роста и коэффициент роста в динамических рядах с равноотстоящими уровнями рассчитываются по формуле средней геометрической простой

– цепные коэффициенты роста;

– цепные темпы роста.

Эти формулы могут быть приведены к следующему виду:

Для того чтобы определить, на сколько процентов текущий уровень показателя больше или меньше значения предшествующего или базисного уровня, рассчитываются темпы прироста. Они исчисляют путем вычитания 100% из соответствующих темпов роста:

- цепные темпы прироста:

- базисные темпы прироста:

Значения темпов прироста можно получить и другим способом, а именно через отношение соответствующих абсолютных приростов к уровням показателей, принятым за базу сравнения:

- цепные темпы прироста:

- базисные темпы прироста:

Средний темп прироста рассчитывается аналогичным образом: из среднего темпа роста вычитаются 100%:

Пример 9.7.В таблице приведены рассчитанные коэффициенты роста, темпы роста и прироста показателя, характеризующего среднемесячный размер выплаченного компанией страхового возмещения за период с января по июнь.

По формуле средней геометрической простой определим среднемесячный коэффициент роста показателя за период с февраля по июнь:

или

Средний темп роста, соответственно, равен 101,1%. Следовательно, в среднем ежемесячно размер выплат страхового возмещения увеличивался в 1,011 раза, или на 1,1%.

Если известны средние темпы (или коэффициенты) роста за некоторые неравные отрезки времени, то средний темп роста за весь период исчисляется по формуле средней геометрической взвешенной

где 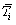– средний темп роста за i-й период времени;

t_i – длина i-го периода.

Пример 9.8.Среднегодовые коэффициенты роста числа страховых компаний в одной из областей России составили за период 1991-1995 гг. – 1,18; 1995-2000 гг. – 1,24; 2000-2004 – 1,56. Определим среднегодовой коэффициент роста числа страховых компаний за весь период с 1991 по 2004 гг.

Решение:

Таким образом, за период с 1991 по 2004 гг. среднегодовой темп роста числа страховых компаний в одной из областей России составил 131,1%, соответственно, среднегодовой темп прироста – 31,1%.

Для более полного анализа динамики расчет цепных показателей роста и прироста уровней динамического ряда часто сопровождаются указаниями абсолютных значений 1% прироста.

Абсолютное значение 1% прироста (А_i) определяется как отношение значения абсолютного прироста показателя к его темпу прироста в i-й момент времени

В последней графе таблицы примера 9.7 рассчитаны цепные абсолютные значения 1% прироста.

Дата добавления: 2014-04-24; просмотров: 1067; Нарушение авторских прав

Мы поможем в написании ваших работ!