Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли

Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику – среднюю ошибку выборки (m).

В теории выборочного наблюдения выведены формулы для определения m, которые индивидуальны для разных способов отбора (повторного и бесповторного), типов используемых выборок и видов оцениваемых статистических показателей.

Например, если применяется повторная собственно случайная выборка, то m определяется как:

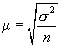– при оценивании среднего значения признака;

– если признак альтернативный, и оценивается доля.

При бесповторном собственно случайном отборе в формулы вносится поправка

– для среднего значения признака;

– для доли.

Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.

Предельная ошибка выборки (D) равна t-кратному числу средних ошибок выборки (в теории выборки принято коэффициент t называть коэффициентом доверия):

D = t m.

Если ошибку выборки увеличить в два раза (t=2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае – двойной средней ошибки) – 0,954. Если взять t=3, то доверительная вероятность составит 0,997 – практически достоверность.

Уровень предельной ошибки выборки зависит от следующих факторов:

- степени вариации единиц генеральной совокупности;

- объема выборки;

- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);

- уровня доверительной вероятности.

Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше – по таблице распределения Стьюдента (Приложение 1).

Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.

Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:

Итак, определение границ генеральной средней и доли состоит из следующих этапов:

¨ нахождение в выборке среднего значения признака (или доли);

¨ определение m в соответствии с выбранной схемой отбора и вида выборки;

¨ задание доверительной вероятности Р и определение коэффициента доверия t по соответствующей таблице;

¨ вычисление предельной ошибки выборки D;

¨ построение доверительного интервала для средней (или доли).

Дата добавления: 2014-04-24; просмотров: 910; Нарушение авторских прав

Мы поможем в написании ваших работ!