Вопрос 2. Ошибки выборки

При выборочном наблюдении должна быть обеспечена случайностъ отбора единиц. Каждая единица должна иметь равную с другими возможность быть отобранной. Именно на этом основывается собственно-случайная выборка.

Собственно-случайная выборка- отбор единиц из всей генеральной совокупности без предварительного ее разделения на какие-либо группы посредством жеребьевки (преимущественно) или какого-либо иного подобного спосо­ба, например, с помощью таблицы случайных чисел.

Количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки.

Доля выборки- отношение числа единиц выборочной со­вокупности к числу единиц генеральной совокупности:

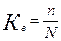
Применяя выборочный метод в статистике, обычно используют два основных вида обобщающих показателей: среднюю величину ко­личественного признака и относительную величину альтернативного признака, т.е. долю или удельный вес единиц в статистической сово­купности, которые отличаются от всех других единиц этой сово­купности только наличием изучаемого признака.

Выборочная доля (w), или частость, определяется отношением числа единиц, обладающих изучаемым признаком т, к общему числу единиц выборочной совокупности п:

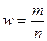
Для характеристики надежности выборочных показателей применяют среднюю и предельную ошибки выборки.

При случайном повторном отборе средние ошибки рассчитывают по следующим формулам:

1) для средней количественного признака

2) для доли, т.е. альтернативного признака

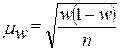
При случайном бесповторном отборе в приведенные выше формулы расчета средних ошибок выборки необходимо подко­ренное выражение умножить на 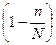. Следовательно, для бесповторной вы­борки расчетные формулы средней ошибки выборки примут такой вид:

1) для средней количественного признака

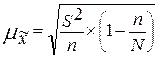
2) для доли (альтернативного признака)

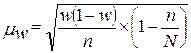
Механическая выборка- выборка, при которой отбор единиц в выборочную совокупность из генеральной, разбитой по ней­тральному признаку на несколько равных групп, произво­дится таким образом, что из каждой такой группы в выборку отбирается лишь одна единица. Чтобы избежать систематической ошибки, отбираться должна единица, которая находится в середине каждой группы.

При организации механического отбора единицы совокуп­ности предварительно располагают в определенном порядке, например, по алфавиту, местоположению, в порядке возрастания или убывания значений какого-либо по­казателя, не связанного с изучаемым свойством, и т.д.

Ошибки выборки при механическом отборе единиц вычисляют по формулам собственно-случайной бесповторной выборки:

1) для средней количественного признака

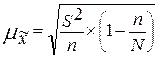
2) для доли (альтернативного признака)

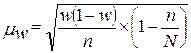
Для отбора единиц из неоднородной совокупности применя­ется, так называемая типическая выборка.

Типическая выборка– это способ отбора, который осуществляется на основе распределения количества отобранных единиц между группами, которые присутствуют в генеральной совокупности.

При определении средней ошибки типической выборки в ка­честве показателя вариации выступает средняя из внутригрупповых дисперсий.

Среднюю ошибку типической выборки находят по формулам:

1) для средней количественного признака

А) повторный отбор:

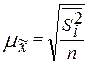
Б) бесповторный повтор

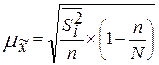
2) для доли (альтернативного признака)

А) повторный отбор:

Б) бесповторный повтор

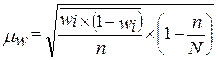
где 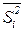- средняя из внутригрупповых дисперсий по вы­борочной совокупности;

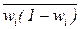- средняя из внутригрупповых дисперсий доли (альтернативного признака) по выборочной совокупности.

Серийная выборкапредполагает случайный отбор из генеральной совокупности не отдельных единиц, а их равновеликих групп (гнезд, серий) с тем, чтобы в таких группах подвергать наблюдению все без исключения единицы.

Среднюю ошибку выборки для средней количественного при­знакапри серийном отборе находят по формулам:

1) повторный отбор:

2) бесповторный отбор:

где r– число отобранных серий ;

R – общее число серий;

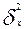- межгрупповая дисперсия серийной выборки, вычисляемая сле­дующим образом:

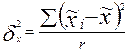
где — средняя i- й серии;

— общая средняя по всей выборочной совокупности.

Средняя ошибка выборки для доли (альтернативного при­знака) при серийном отборе:

1) повторный отбор:

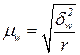
2) бесповторный отбор:

где - межгрупповая (межсерийная) дисперсия доли серийной вы­борки,определяемая по формуле:

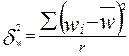
где 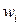— доля признака в i-й серии;

— общая доля признака во всей выборочной совокупности.

В практике статистических обследований помимо рассмот­ренных способов отбора применяется их комбинация (комбинированный отбор).

---

<== предыдущая страница	|	следующая страница ==>
Вопрос 1. Понятие о выборочном наблюдении	|	Вопрос 3. Распространение выборочных результатов на генеральную совокупность

---

Дата добавления: 2014-03-11; просмотров: 711; Нарушение авторских прав

---

Поделиться с ДРУЗЬЯМИ:

Мы поможем в написании ваших работ!