Сумма двух случайных величин

Z=X+Y

Мат. ожидание

M(Z)=M(X)+M(Y) или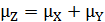

Дисперсия

.

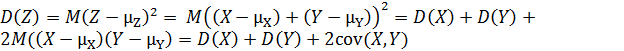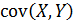–ковариация или корреляционный момент рассматриваемых случайных величин

Коэффициент корреляции

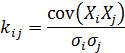
Для независимых случайных величин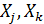

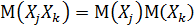
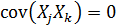
Если 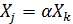, то ,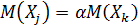

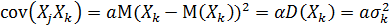
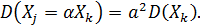
Отсюда

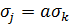
При этом коэффициент корреляции

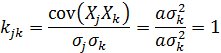
Итак, для линейно зависимых случайных величин коэффициент корреляции по модулю равен 1.

Для нормального распределения (но не для любого) из 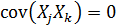следует независимость .

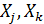Функция распределения суммы случайных величин

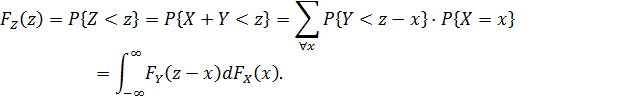
Данный интеграл называется интегралом типа свертки.

Для дискретной случайной величины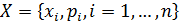

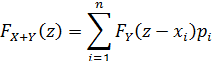
Именно такую операцию мы выполняли при определении вероятности дефицита мощности при биномиальном распределении числа отключенных блоков.

В общем случае

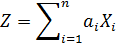
Математическое ожидание

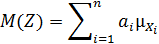
Дисперсия

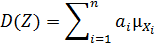
6.3 ДЗ. Комп:

Получить вероятность и МО дефицита мощности при детерминированной нагрузке:

1. через вероятностный ряд генерации;

2. через формульное аналитическое представление;

3. через дополнительную случайную величину (небаланс мощности,
N=Р_н – Р_расп), рассматривая ее как нормально распределенную величину

4. Построить график изменения МО дефицита мощности от
q 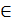(0.2 –0.12);

5. На одном графике построить интегральную и дифференциальную функции распределения небаланса мощности N=Р_н – Р_расп с вероятностным рядом генерации, а также кривую плотности распределения N, считая ее нормально распределенной величиной. Какой вывод можно сделать относительно аппроксимации реального распределения небаланса мощности N=Р_н – Р_расп нормальным?

Дата добавления: 2014-05-02; просмотров: 486; Нарушение авторских прав

Мы поможем в написании ваших работ!