
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Лекция 6. Детерминированная нагрузка
6.1 Детерминированная нагрузка.
При 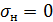 встроенная в Excel функция нормального распределения НОРМ.РАСП(x; μ; σ; i) не работает. В этом случае необходимо поставить ловушку на нулевую дисперсию. Детерминированная величина может рассматриваться как случайная с функцией распределения, имеющей единичный скачок в точке ее значения. В этом случае желательно создать собственную процедуру расчета нормального распределения, учитывающую «ловушку», например, в среде VBA (Visual Basic for Applications) такую:
встроенная в Excel функция нормального распределения НОРМ.РАСП(x; μ; σ; i) не работает. В этом случае необходимо поставить ловушку на нулевую дисперсию. Детерминированная величина может рассматриваться как случайная с функцией распределения, имеющей единичный скачок в точке ее значения. В этом случае желательно создать собственную процедуру расчета нормального распределения, учитывающую «ловушку», например, в среде VBA (Visual Basic for Applications) такую:
Public Function VerFDist(x, MO, sko) As Double 'Интегральная Функция нормального распределения
VerFDist = 0:
If (sko = 0 And x >= MO) Then VerFDist = 1
If (sko = 0 And x < MO) Then VerFDist = 0
If (sko < > 0) Then VerFDist = НОРМ.РАСП(x; MO; sko; 1)
End Function
При априори заданной детерминированной нагрузке столбец вероятности дефицита мощности при заданной располагаемой мощности можно получить используя логическую функцию «Если(Pн<Ррасп; 0;1)», а столбец МО дефицита мощности при заданной располагаемой мощности , используя «Если(Pн<Ррасп; 0; Pн-Ррасп)».
При детерминированной нагрузке единственной случайной величиной является располагаемая мощность (число отключенных блоков). Дефицит мощности наблюдается, если Pн 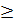 Ррасп
Ррасп
Отсюда вероятность дефицита мощности можно определить исходя из определения функции распределения
P=1-B(Pн/Pбл; n; q,1),
где B() – функция биномиального распределения.
МО дефицита мощности при детерминированной нагрузке может быть определено на базе биномиального распределения по формуле (5.2)
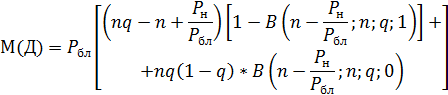
| <== предыдущая страница | | | следующая страница ==> |
| Оптимальный резерв мощности в концентрированной ЭЭС | | | Сумма двух случайных величин |
Дата добавления: 2014-05-02; просмотров: 409; Нарушение авторских прав

Мы поможем в написании ваших работ!