
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Оптимальный резерв мощности в концентрированной ЭЭС
Формула Марковича
Одним из ярких примеров необходимости и применимости вероятностных характеристик небаланса мощности в ЭЭС является задача об оптимальном резерве мощности в концентрированной энергосистеме.
Увеличение резерва приводит к повышению надежности электроснабжения потребителя, но это связано с дополнительными капиталовложениями. В качестве критерия оптимальности в экономических расчетах, как правило, принимается минимум приведенных затрат. Если составляющие затрат имеют вероятностный характер, то данный критерий преобразуется в минимум математического ожидания (МО) приведенных затрат.
От величины располагаемого резерва мощности 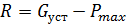 зависит вероятностный ущерб от недоотпуска электрической энергии
зависит вероятностный ущерб от недоотпуска электрической энергии
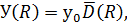 где
где 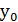 – удельный ущерб от недоотпуска электроэнергии;
– удельный ущерб от недоотпуска электроэнергии; 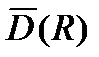 – МО дефицита мощности. В общем случае
– МО дефицита мощности. В общем случае 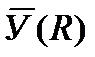 имеет более сложный функциональный характер, который, безусловно, учитывается в программных реализациях.
имеет более сложный функциональный характер, который, безусловно, учитывается в программных реализациях.
Отсюда задача об оптимальном резерве мощности имеет вероятностный характер и заключается в отыскании такого резерва R, который минимизирует МО приведенных затрат,
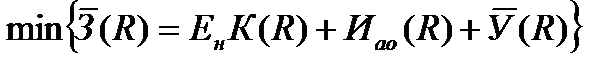 .
.
В упрощенной постановке можно принять линейную модель капиталовложений и ежегодных издержек 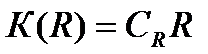 ,
,
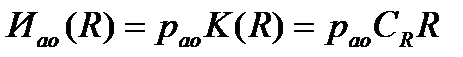 .
.
Реальный годовой график максимальной нагрузки можно представить максимальной нагрузкой 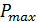 и числом часов использования максимума
и числом часов использования максимума  . В свою очередь,
. В свою очередь, 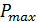 обладает неопределенностью и может рассматриваться как случайная величина с МО
обладает неопределенностью и может рассматриваться как случайная величина с МО 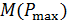 и дисперсией
и дисперсией 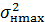 . В этом случае
. В этом случае
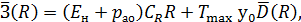
Электропотребление можно представить не только через, например, суточную максимальную мощность, но и через текущую мощность 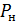 с заданным мат. ожиданием
с заданным мат. ожиданием 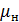 и дисперсией
и дисперсией 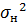 (
( 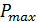 и
и 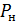 – это две разные случайные величины. Как правило,
– это две разные случайные величины. Как правило, 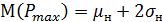 . В этом случае длительность расчетного периода равна 8760 ч.
. В этом случае длительность расчетного периода равна 8760 ч.
Дефицит мощности имеет место, если мощность нагрузки превышает установленную, с учетом вновь вводимого резерва мощности – располагаемую мощность 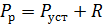 .
.
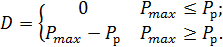
Рассмотрим новую случайную величину N = 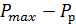 (сдвиг по оси мощности на величину
(сдвиг по оси мощности на величину  ). Она, как и
). Она, как и 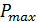 , описывается нормальным распределением с МО
, описывается нормальным распределением с МО 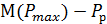 и дисперсией
и дисперсией 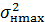
В этом случае мат. ожидание дефицита мощности
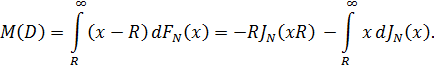
| (5.3) |
где 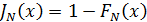 – дополнительная функция распределения.
– дополнительная функция распределения.
Интеграл
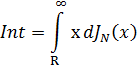
можно представить в ином виде, используя разложение интеграла «по частям», принимая
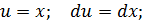

Отсюда
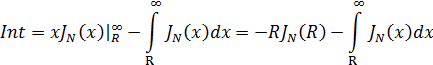
Подставляя полученное выражение в (5.3), получаем
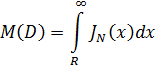
т.е. МО дефицита определяется площадью под кривой дополнительной функции распределения 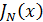 (рис. 1.1). В результате
(рис. 1.1). В результате
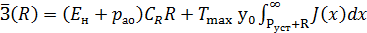 .
.
Оптимальный резерв мощности определяется из условия равенства нулю производной по R от функции приведенных затрат
| J(x) |
| x |
| Руст+R |
| Jопт |
| Рис. 5.1 Оптимальный резерв мощности |
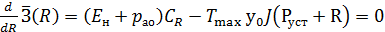
Отсюда оптимальный резерв мощности должен быть таким, чтобы вероятность дефицита мощности удовлетворяла условию
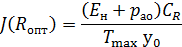
т.е. оптимальная вероятность дефицита мощности пропорциональна удельным капиталовложениям и обратно пропорциональна удельному ущербу. Данное соотношение носит название критерия Марковича []. Нетрудно видеть, что для определения численной величины оптимального резерва мощности необходимо знать параметры (МО и дисперсию) функции распределения максимальной мощности
Пример 1.1. Пусть CR=200 $/кВт; у0=1$/кВт·ч; Тmax=6000ч; отчисления на амортизацию и обслуживание рао=9%.
При оптимальном резерве 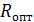 вероятность дефицита мощности
вероятность дефицита мощности 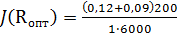 =0,007 (в течение года допускается 0,007∙8760=61 час состояния дефицита мощности). При заданных условиях оптимальный индекс надежности (вероятность бездефицитной работы)
=0,007 (в течение года допускается 0,007∙8760=61 час состояния дефицита мощности). При заданных условиях оптимальный индекс надежности (вероятность бездефицитной работы)  =0,993 , т.е. оптимальный резерв мощности должен быть таким, чтобы обеспечить индекс надежности =0,993.
=0,993 , т.е. оптимальный резерв мощности должен быть таким, чтобы обеспечить индекс надежности =0,993.
Пусть при Рр=1100 МВт МО нагрузки μнmax=1000 МВт, σнmax=100 МВт. При оптимальной вероятности отсутствия дефицита мощности (индекс надежности)
 =
= 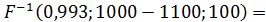 146 МВт.
146 МВт.
ДЗ:
1. Рассмотреть оптимизационную задачу (в Excel-е использовать процедуру «Поиск решения»):
По критерию минимальных приведенных затрат определить оптимальный дополнительный резерв Rопт мощности. Приведенные затраты
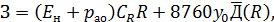
где 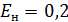 – нормативный коэффициент эффективности;
– нормативный коэффициент эффективности; 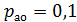 – отчисления на амортизацию и обслуживание;
– отчисления на амортизацию и обслуживание; 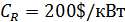 – удельные капиталовложения в резервную мощность; у0=1$/кВтч – удельный ущерб от недоотпуска электроэнергии потребителям;
– удельные капиталовложения в резервную мощность; у0=1$/кВтч – удельный ущерб от недоотпуска электроэнергии потребителям; 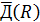 – зависящее от МО дефицита мощности.
– зависящее от МО дефицита мощности.
2. Графически изобразить зависимость З(R).
3. Рассмотреть объединенную систему «нагрузка + генерация» и нормально распределенную случайную величину – небаланс мощности 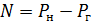 с математическим ожиданием
с математическим ожиданием 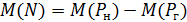 =
=  и дисперсией
и дисперсией 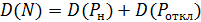 . Определить вероятность и МО дефицита мощности (
. Определить вероятность и МО дефицита мощности ( 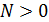 ). Сравнить результаты с ранее полученными при биноминальном распределении отключенных генераторах.
). Сравнить результаты с ранее полученными при биноминальном распределении отключенных генераторах.
| Объединенная система | |||||
| Исх. Данные | q | n | Рбл | Руст | |
| Генерация | 0,1 | ||||
| Нагрузка | Мат.ожид. | Дисперсия | sigma | ||
| Генерация | M( Роткл) | D( Роткл) | sigma | ||
| Роткл | 116,19 | ||||
| Небаланс | МО( N) | D( N) | sigma | ||
| N | -100 | 177,482 | |||
| Модель | P(деф) | М(деф) | |||
| N | 0,28657 | 31,756 | |||
| дискр.ряд | 0,28113 | 32,4429 | |||
| Ошибка | 1,90% | 2,16% |
При
| <== предыдущая страница | | | следующая страница ==> |
| Лекция 5. Оптимальный резерв мощности | | | Лекция 6. Детерминированная нагрузка |
Дата добавления: 2014-05-02; просмотров: 386; Нарушение авторских прав

Мы поможем в написании ваших работ!