Причины прогрессивной эволюции

________________________________

На основе успехов ньютоновской механики сложилась определенная система взглядов, получившая название лапласовского (механического) детерминизма. Согласно Лапласу, если заданы начальные условия (Координаты и импульсы всех частиц системы), действующие на систему неограниченно, в прошлое и будущее.

Рис. 2.5 – Изменение состояния системы в зависимости от эффективного времени t/t

Дадим определения. Динамическими называются такие закономерности, которые однозначно определяют состояние системы в любой момент времени по полному набору параметров состояния в некоторый момент времени. Вероятностными (или статическими) называются закономерности, на основании которых однозначно определяются вероятности появления определенных значений случайных величин.

С точки зрения лапласовского детерминизма все закономерности в природе – динамические, и если наука не находит таких закономерностей, то это означает, что неточно заданы какие-либо параметры состояния (например, внутренние силы системы).

Рассмотрим в качестве примера полет ракеты. Динамическое воздействие определяется силой гравитации и силой тяги двигателя ракеты. Стохастические воздействия зависят от атмосферных вихрей, от флуктуаций процесса сгорания топлива. Стохастическое – нерегулярное, имеющее вероятностный характер, внешне неотличимое от случайного воздействия. Очевидно, что динамическое воздействие превосходит стохастическое. Однако, несмотря на свою малость, стохастические воздействия могут привести к тому, что ракета не достигнет запланированной области.

Если описывать зависимость поведения любой системы от времени, то динамическое поведение будет соответствовать плавной линии на рис.2.5. В тот момент времени, когда становится существенным стохастическое воздействие, система может непредсказуемым образом изменить свое поведение в зависимости от величины стохастического воздействия. В этом случае ее поведение будет описываться одной из возможных кривых, выходящих из одной точки В. Состояние, в котором при заданных начальных условиях и силах эволюция системы может пойти по-разному, называется бифуркационным состоянием или точкойбифуркации.

Для указанных закономерностей поведения можно привести интересную интерпретацию – механическое устройство, подобное «машине катастроф» Зимана (рис. 2.6). Оно состоит из рычага АВ, шарнирно соединенного с основанием (точка А), и пружин ВС и СД, одна из которых (ВС) связана с рычагом АВ и основанием, а другая (БД) имеет один свободный конец (Д), к которому должна быть приложена сила.

«Катастрофа» наступает, если попытаться перевести точку В из верхней полуплоскости, ограничиваемой продолжениями отрезка АС, в нижнюю полуплоскость. Когда точки А, В и С окажутся на одной линии (точка Д может уже находиться ниже указанной линии), то пружина ВС испытывает максимальное растяжение. Затем происходит срыв («катастрофа») и стремительное движение точки В в новое положение (ниже линии АС).

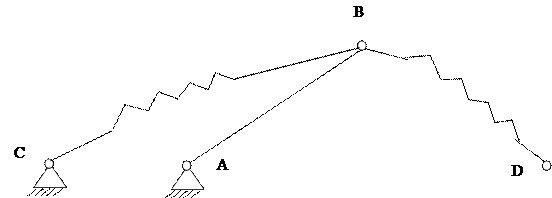Рисунок 2.6. – Машина катастроф с одной степенью свободы.

Состоянию срыва соответствуют разные положения точки Д, определяемые величиной и направлением прилагаемых к ней усилий. При этом можно построить так называемую «кривую катастроф», параметры которой зависят от геометрических и упругих характеристик системы.

Аналогия с «теорией перестройки» здесь, на наш взгляд, налицо: управляемая система соответствует контуру АВС, растяжение пружины ВС характеризует степень неудовлетворительности состояния системы, близость ее к наихудшему состоянию. Однако в указанном предельном положении (точка В лежит на прямой АС) сопротивление перемещению невелико, здесь нарушается регулярная структура, и в этом смысле имеет место хаос. Таким образом, поведение «машины катастроф» согласуется с положениями «теории перестройки». Попытаемся теперь выяснить условия, определяющие различный характер процесса бифуркации.

Согласно изложенному, структура нарушается тогда, когда точки А, В, С расположатся по одной прямой, очевидно, что пружина ВС при этом максимально растянута. Специфика данного положения заключена в том, что при любом направлении выхода из него длина пружины ВС уменьшается, а катастрофа выражается тем, что после срыва внутренние свойства системы АВС обуславливают потерю управляемости и стремительный переход в новое функциональное состояние.

В особом положении система АВС (без учета действия пружины ВД) пребывает в состоянии неустойчивого равновесия. Но данное состояние вполне можно продлить как угодно долго, расположив пружину ВД также вдоль линии АС и соответствующим образом растянув ее, - тогда сила натяжения этой пружины может обеспечить устойчивость особого положения.

Если же, перемещая точку Д вдоль линии АС, мы будем ослаблять натяжение указанной пружины, то направление срыва и стремительного перемещения точки В будет определено случайными факторами (например, минимальными вибрациями основания), мало влияющими в обычных состояниях. При этом наличие дополнительного (пусть весьма маломощного) привода в точке А обусловит отсутствие случайности в определении направления движения звена АВ.

Процесс бифуркации при различных условиях может иметь как катастрофический, так и вполне управляемый характер, что определяется натяжением пружины ВД и траекторией точки Д. Если из положения, изображенного на рис. 2.6. данную точку перемещать вдоль линии ВД, увеличивая расстояние между этими точками, то точка В будет приближаться к линии СА и соответственно к другой полуплоскости, определяемой этой линией, затем неизбежно произойдет срыв, и вследствие наличия упругости будут наблюдаться колебания около устойчивого состояния. Отметим, что перед срывом точки В и Д будут располагаться в разных полуплоскостях. Некатострофический переход возможен, если пружина ВД сильно растянута и упругость пружины СВ мало влияет на характер процесса.

Основываясь на изложенном, хотелось бы сделать несколько замечаний. Во-первых, следует отметить, что характер процесса бифуркации существенно зависит от свойств системы, как-то: от наличия в ней некоторых внутренних сил, характер действия которых определяется структурой и возможностью изменения этой структуры в особых точках.

Во-вторых, можно указать на важность характера внешних сил, их точки приложения, величины и траектории действия - напомним, что катастрофический характер бифуркации связан с возможностью расположить точки В и Д по разные стороны от линии АС, разделяющей две полуплоскости. Если же в момент происхождения особой точки внешняя сила способна уравновесить внутреннюю, обусловливающую катастрофичность, то процесс бифуркации управляем.

Наконец, хотелось бы отметить роль соотношения между характеристиками передаточных элементов (пружин), осуществляющих взаимодействие между элементами системы и внешними возмущениями. (Если вместо пружины ВД будет просто жесткий стержень, то «катастрофа» в принципе невозможна.)

Безусловно, рассматриваемая механическая система весьма проста, однако, по нашему мнению, она в какой-то степени отражает поведение гораздо более сложных систем, и это обусловлено несколькими обстоятельствами. Прежде всего отметим, что даже вполне сложная система с разветвленной структурой в точке бифуркации имеет, как правило, одну главную особенность, главное противоречие. Собственно, термин «синергия», характеризующий совместное действие многих элементов системы, связан с тем, что эти элементы становятся подчинены одному или нескольким параметрам порядка.

Далее укажем на то обстоятельство, что рассмотренная модель вполне характеризует важность соотношения внешних и внутренних сил, действующих на систему, с учетом их величины, точки приложения и направления действия. Кроме того, здесь показана возможность существования такой ситуации, что в точке бифуркации выбор подвержен лишь случайным факторам, а для целенаправленного осуществления выбора может быть необходим дополнительный (в данном случае расположенный в точке А) двигатель.

Здесь уместно остановиться на термине «диссипативные системы», применяемом И. Пригожиным. Если внутренние силы, по сравнению со внешними, весьма велики, то система может считаться консервативной. В этом случае она подвержена действию законов сохранения (энергии, массы). Если же внешние силы значительно превышают внутренние и, кроме того, передаточные элементы (пружины) обладают существенной жесткостью, то катастрофический процесс бифуркации уступает место вполне управляемому процессу. По нашему мнению, диссипативными следует считать системы, где нет существенного преобладания внешних или внутренних сил друг относительно друга. В указанном смысле рассматриваемая механическая модель может отвечать термину «диссипативная».

Однако отметим, что описанное механическое устройство действительно не отражает многих свойств сложных систем. Одно из этих свойств связано с тем, что внешние силы подчас в принципе не могут обусловить движение системы из точки бифуркации в некотором предписанном направлении. Следует также указать на случаи, когда особые точки могут образовывать целые связанные области. Речь, в частности, может идти об устройствах с более высоким, чем единица, числом степеней свободы.

Приведем еще один пример. Рассмотрим реальный газ, находящийся в сосуде при нормальных условиях. Движение молекул между столкновениями подчиняется законам классической механики и носит динамический характер. Строго говоря, столкновения определяются силами Ван-дер-Ваальса, которые подчиняются закономерностям квантовой механики.

Движение бильярдных шаров и даже движение галактик аналогично движению молекул газа. До столкновения движение этих систем описывается динамически, различны лишь времена динамического поведения t. Для молекул это время составляет 10^-8 с, а для космических объектов – порядка 10⁹ лет.

В рамках классической термодинамики были получены крайне важные теоретические и практические результаты. Однако классическая термодинамика имеет нерешенные проблемы, которые определяют границы ее применимости. Во-первых, эта наука рассматривает лишь изолированные системы. Во-вторых, она не рассматривает скорости протекания термодинамических процессов и факторы, влияющие на эти скорости. Все это приводит к тому, что классическая термодинамика не в состоянии описать эволюцию реальной системы, живой или неживой. Описанием эволюции систем занимается неравновесная термодинамика, которая, в соответствии с принятой сегодня терминологией, является одной из ветвей нового направления в науке - синергетики. В 80-е годы 20 века синергетика сформировалась как научное направление, ориентированное на поиск законов эволюции открытых неравновесных систем любой природы. Слово «синергетика» происходит от греческого слова synergetikos – совместный, согласованно действующий. Термин «синергетика» был предложен в 1977 г. Г. Хакеном. Он отражает тот факт, что процессы упорядочивания в сложноорганизованных неравновесных системах возникают благодаря взаимодействию элементов системы [203, 212].

Показано, что в точках бифуркации может происходить смена пространственно-временной организации системы. Система «скачком» переходит из хаотического в организованное состояние. Говорят, что в системе произошла самоорганизация. Под самоорганизацией понимаются процессы упорядочивания, происходящие в системе за счет самосогласованного действия ее элементов. Примерами самоорганизации могут служить процессы объединения птиц в стаю, людей на улице в очередь у магазина, предпринимателей в ассоциацию.

Классическим примером самоорганизации в физической системе является эффект Бенара возникновение ячеек правильной геометрической формы (ячеек Бенара) в слое жидкости (силиконового масла), помещенном между горячей нижней и холодной верхней пластинами (рис. 2.7).

При незначительной разности температур между пластинами преобладающим процессом является вязкость жидкости, жидкость в целом неподвижна, все тепло передается от нижней пластины к верхней за счет теплопроводности. С ростом разности температур более теплая жидкость снизу расширяется и стремится поменять местами с более холодными, имеющими большую плотность слоями, расположенными сверху. Состояние, когда снизу находится легкая, а сверху тяжелая жидкость, является неустойчивым.

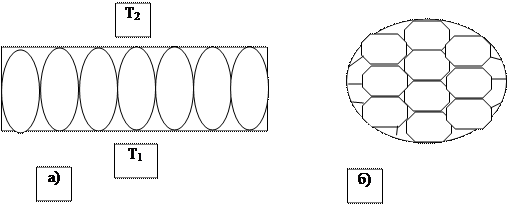Рис. 2.7. – Образование ячеек Бенара: а - вид сбоку; в – вид сверху [212]

Когда разность температур достигнет критического значения, в жидкости возникает макроскопическая структура, сильно зависящая от окружающих условий. Если слой жидкости тонкий, то возникшая структура состоит из цилиндрических вихрей (ячеек), изображенных на рис.2.7,а. Если слой жидкости не является тонким и отсутствует верхняя охлаждаемая пластина, то формируется верхняя охлаждаемая пластина, то формируется очень похожая на пчелиные соты структура из шестигранных призматических ячеек (рис. 2.7, в). Жидкость поднимается в центре каждой ячейки и опускается вблизи ее граней.

Согласованный эффект, проявляющийся при возникновении ячеек Бенара, разрушается при дальнейшем повышении температуры, что приводит к полностью неупорядоченному, хаотическому состоянию.

На основании этого сформулируем выводы. По мере увеличения отклонения от равновесия, при определенных критических значениях внешних параметров, система переходит в качественно новое состояние, которое характеризуется более высоким уровнем организации, когда возникают устойчивые пространственные неоднородные структуры. Процесс возникновения этих структур называется самоорганизацией, а возникающие структуры называются диссипативными, поскольку они могут существовать лишь при постоянной диссипации (рассеянии) энергии, поступающей из внешней среды. Сущность процесса самоорганизации заключается в формировании в изначально однородной среде упорядоченных в пространстве и (или) времени состояний, т.е. в переходе от хаоса к порядку.

Явление Бенара ярко демонстрирует роль диссипативных процессов как основного фактора для осуществления самоорганизации среды. процесс диссипации (рассеяния) тепловой энергии приводит при определенных условиях к формированию на макроуровне пространственных структур строгой геометрической формы, т.е. к возникновению порядка из хаоса.

Таким образом, по мере удаления системы от равновесия в ней спонтанно, вероятностным образом возникают диссипативные структуры, т.е. система может произвольно переходить от более низкого уровня сложности к более высокому. Это означает, что можно говорить о прогрессивной эволюции открытых неравновесных систем.

Первое сообщение о возможности образования пространственных структур в однородной среде было опубликовано в 1952 году А. Тьюрингом, наблюдавшим этот процесс в химических реакциях с диффузией. Глубокое понимание природы явлений, имеющих место в этих реакциях, пришло значительно позже в результате исследований, проведенных в брюссельской научной школе, руководимой И.Р. Пригожиным. В 1977 г. И.Р. Пригожин был удостоен Нобелевской премии по химии за создание теории диссипативных структур.

Перечислим условия, необходимые для запуска механизма самоорганизации:

1. система должна быть диссипативной (или открытой), что позволяет ей обмениваться энергией и веществом с окружающей средой;

2. отклонение от равновесия, вызванное внесением энергии в систему, должно превышать критическое значение;

3. динамические уравнения, описывающие поведение системы, должно быть нелинейным;

4. процессы на уровне элементов системы должны происходить согласованно.

Выводы неравновесной термодинамики, описывающей процессы самоорганизации, дают возможность, пусть качественно, но ответить на вопрос о механизме возникновения жизни и прогрессивном характере эволюции неживого и живого вещества.

Согласно выводам неравновесной термодинамики, высокоорганизованные формы неживой и живой материи могут возникать сами по себе, даже если диссипативной системе не поставлена кем-либо опережающая цель.

Космические, геологические, биологические и другие эволюционные процессы, состоящие в возникновении порядка из хаоса, осуществляются за счет передачи положительной энтропии в окружающую среду. В точке бифуркации возможно возникновение различных состояний, среди которых затем, путем отбора, производится выбор наиболее устойчивых состояний. Естественный отбор, который характерен не только для живой материи, создает направленную эволюцию. «Возникновение неоднородностей – звезд и галактик – вследствие гравитационной неустойчивости означает конкуренцию и естественный отбор. Гравитационные неоднородности конкурируют друг с другом за конденсируемый материал» [213]

Поясним, как действует естественный отбор на уровне открытых систем. Внутренняя устойчивость любой системы предполагает ее постоянное противодействие внешним факторам, стремящимся вывести систему из состояния неустойчивого равновесия и привести ее в состояние устойчивого равновесия (с максимумом энтропии). Внешние воздействия стремятся изменить состояние системы. Любая неравновесная система стремится сохранить состояние неустойчивого равновесия, складывающегося в каждый данный момент времени. Неравновесные состояния, возникающие в системах за счет случайных флуктаций, оказываются в подавляющем большинстве случаев неустойчивыми не потому, что система стремится обратно к равновесию, а потому, что организация системы недостаточно эффективна, чтобы стабилизировать такое состояние. Таким образом, можно сделать вывод, что борьба за неравновесное состояние свойственна всем материальным взаимодействиям. Именно это дает основание определить общезначимый (во всех сферах) критерий прогресса: система, сумевшая стабилизировать более высокие значения неравновесия со средой, обладает более совершенными средствами управления, и данное обстоятельство задает направление прогрессивного развития [203].

Дата добавления: 2014-05-02; просмотров: 418; Нарушение авторских прав

Мы поможем в написании ваших работ!