
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Формальная (математическая) интерпретация эволюционных и революционных процессов
_____________________
Первой областью науки, где пытались определить и описать эволюционные закономерности, явилось естествознание.
Было замечено, например, что рост популяций происходит неравномерно: сначала медленно, затем бурно с постепенным замедлением, приближаясь к некоторому пределу.
Установлено, что рост популяций, как и другие процессы развития, идет по S-образной (логической) кривой. Этот закон в 1845 году был открыт Р.Перле, американским биологом и демографом. Кривая Перле симметрична относительно точки перегиба (рис. 2.8 ) и имеет вид [200]:
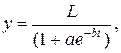 (2.5)
(2.5)
где L, a, b – константы, t – время
Для более точной апраксимации реальных процессов английским статистиком и математиком Б. Гомперцем предложена кривая, ассиметричная относительно точки перегиба (рис. 2.9):
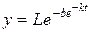 , (2.6)
, (2.6)
где L, b, k – константы, t – время
Закономерности, описываемые уравнениями (2.5) и (2.6) наблюдаются и в технике.
Изменения параметров машин и других технических систем описываются различными математическими зависимостями: линейными ( 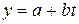 ), степенными (
), степенными ( 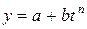 ), полулогарифмическими (
), полулогарифмическими ( 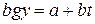 ), экспоненциальными (
), экспоненциальными (  ) и др. В настоящее время известно 130 способов описания закономерностей развития различных систем.
) и др. В настоящее время известно 130 способов описания закономерностей развития различных систем.

Рис. 2.8 Рис. 2.9
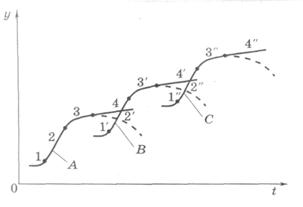
Рис. 2.10
Для развития реальных технических систем характерен многостадийный процесс. Статистические данные изменения тех или иных параметров больших технических систем отражают результаты одновременного воздействия факторов, обусловленных объективными законами. Учитывая одновременное воздействие положительных (прогрессивных) и отрицательных (регрессивных) факторов на процесс развития технических систем, графическое представление многостадийности этого развития может быть представлено семейством единообразных S-образных кривых (А, В, С и т.д.) (рис. 2.10).
Несмотря на индивидуальные особенности, присущие разным техническим системам, эта зависимость имеет характерные участки на каждой составляющей, общие для всех систем. На участке 1 идет медленное развитие системы (ее «детство»); участок 2 соответствует массовому применению, ее совершенствованию («возмужание», «зрелость»); на участке 3 темп развития системы спадает (ее «старость»), система А исчерпывает себя. Далее техническая система А либо деградирует, сменяясь принципиально новой системой В, либо долгое время сохраняет достигнутые показатели (участок 4). Для развития новой системы В характерна точно такая же стадийность, и ей на смену приходит более новая техническая система С и т.д.
В качестве примера на рис 2.11 представлена графическая интерпретация развития скоростных легких военных самолетов [214]. На представленном графике четко видны три стадии развития скоростей легких самолетов: первая стадия – 1930 год, вторая – 1930-1945 годы, третья – после 1945 года.
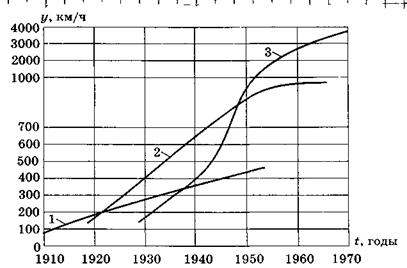
Рис. 2.11
Основным условием повышения скорости летательных аппаратов явилось появление новых двигателей, материалов и улучшение конструкции самолета или планера. Все стадии развития скоростей можно представить общим уравнением:
 (2.7)
(2.7)
где v – скорость, км/ч (t01 – 1914 г., t02 – 1930г., t03 – 1952г.). Коэффициенты этого соотношения приведены в таблице 2.1.
Таблица 2.1.
| Стадии развития | L | a | b | b |
| 0,155 | 1,71 | 0,133 | ||
| 0,142 | 1,104 | 0,0985 | ||
| 0,075 | 5,14 | 0,177 |
Аналогичные примеры приведены в разделе 2.1.
В рассмотренных примерах характерным является то, что в недрах каждой предыдущей стадии развития технической системы зарождается последующая, жизнеспособность и эффективность которой всегда выше предыдущей.
Особенности развития сложных систем заключаются в том, что каждая подсистема, входящая в систему, также проходит все три этапа развития, поэтому S-образные кривые для сложных систем являются интегральными, состоящими из совокупности S-образных кривых всех входящих подсистем. При этом самая «слабая» подсистема, ресурсы которой исчерпываются первыми, обычно тормозит развитие всей системы, поэтому дальнейшее развитие возможно только после ее замены. Например, в развитии самолетостроения в прошлом веке было несколько таких событий: в 20-х годах, когда исчерпала себя аэродинамическая концепция (биплан с неубирающимися шасси, открытая кабина летчика); в 40-х годах – неэффективность воздушного винта при скорости около 700 км/ч.
В экологии логистическое уравнение описывает как эволюционирует популяция из N особей с учетом рождаемости, смертности и количества ресурсов, доступных популяции. Т.е.:
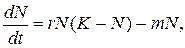 (2.8)
(2.8)
где r и m – характерные постоянные рождаемости и смертности;
К – «несущая способность» окружающей среды.
При любом начальном значении N система со временем выходит на стационарное значение
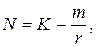 (2.9)
(2.9)
зависящее от разности между несущей способностью среды и отношением постоянных смертности и рождаемости. При достижении этого стационарного значения наступает насыщение: в каждый момент времени рождается столько индивидов, сколько их погибает (см. рис. 2.12). Кажущаяся простота логического уравнения до некоторой степени скрывает сложность механизмов, участвующих в процессе. Ясно, что при учете одних лишь климатических флуктуаций коэффициенты К, m и r нельзя считать постоянными: как хорошо известно, такие флуктуации могут разрушить экологическое равновесие и даже обречь популяцию на полное вымирание. Разумеется, в системе начинаются новые процессы, такие, как создание запасов пищи и образование новых колоний, которые заходят в своем развитии настолько далеко, что позволяют в какой-то мере избежать воздействия внешних флуктуаций.
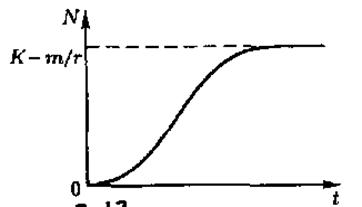
Рис. 2.12 – Эволюция популяции N как функции времени t, описываемая логической кривой. Стационарное состояние N=0 неустойчиво, а стационарное состояние N=K-m/r устойчиво относительно флуктуаций величины N.

Рис. 2.13 – Эволюция всей популяции X как функция времени. Популяция состоит из видов Х1, Х2 и Х3 , возникающих последовательно и соответствующих возрастающим значениям K-m/r
Живые сообщества непрестанно изыскивают новые способы эксплуатации существующих ресурсов или открытия новых (увеличивая тем самым значение параметра К), продления жизни или более быстрого размножения. Каждое экологическое равновесие, определяемое логистическим уравнением, носит лишь временный характер, и логистически заданная экологическая ниша последовательно заполняется серией видов, каждый из которых вытесняет предшествующие, когда его «способность» к использованию ниши, измеряемая величиной K-m/r, становится больше, чем у них (см. рис. 2.13). Таким образом, логистическое уравнение описывает весьма простую ситуацию, позволяющую количественно сформулировать дарвиновскую идею о выживании «наиболее приспособленного»: наиболее приспособленным считается тот вид, у которого в данный момент времени величина K-m/r больше.
Интересно отметить, что кривая на рис. 6.3, показывающая, как последовательно сменяются при увеличении параметра K-m/r периоды роста и пики семейства решений логического уравнения, может также описывать размножение некоторых технологических процедур или продуктов. Открытие или технологическое новшество, появление нового продукта нарушает сложившееся социальное, технологическое или экономическое равновесие. Такое равновесие соответствует максимуму кривой роста техники или продуктов производства, с которыми новшеству приходится вступать в конкуренцию. Приведем лишь один пример. Распространение пароходов привело не только к почти полному исчезновению парусного флота, но и за счет снижения транспортных расходов и повышения скорости перевозок способствовало увеличению спроса на морской транспорт (т.е. увеличению параметра К), что в свою очередь повлекло за собой увеличение численности транспортных судов. Разумеется, ситуация, о которой мы говорим здесь, предельно упрощена и, по предположению, подчиняется чисто экономической логике: технологическое новшество в данном случае лишь удовлетворяет ранее существовавшую потребность, которая остается неизменной. Но в экологии и человеческом обществе имеется немало примеров инноваций, оказавшихся успешными, несмотря на отсутствие предварительной «ниши».
Приведенные примеры подтверждают общность закономерностей развития различных видов технических систем и могут служить научно-обоснованной методикой для изучения процессов развития конкретных технических устройств.
Рассмотрим некоторые типичные бифуркационные диаграммы. В точке бифуркации В термодинамическая ветвь становится неустойчивой относительно флуктуаций (см. рис 2.14). При критическом значении lcrit , управляющего параметра система может находиться в трех различных стационарных состояниях: С, Е и D. Два из них устойчивы, третье неустойчиво. Очень важно подчеркнуть, что поведение таких систем зависит от их предыстории.
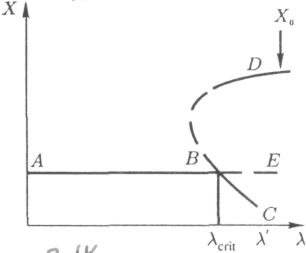
Рис. 2.14 - Бифуркационная диаграмма. Стационарные значения переменной Х представлены на диаграмме как функции параметра бифуркации l. Сплошные линии соответствуют устойчивым, штриховые – неустойчивым стационарным состояниям. Чтобы достичь ветви D, необходимо выбрать начальную концепцию Х0 выше значений Х, лежащих на прямой АВ и порождающих ветвь ВЕ.
Начав с малых значений управляющего параметра и медленно увеличивая их, мы с большой вероятностью опишем траекторию АВС. Наоборот, начав с больших значений концентрации Х и поддерживая постоянным значение управляющего параметра l, мы с высокой вероятностью придем в точку D. Таким образом, конечное состояние зависит от предыстории системы. До сих пор история использовалась при интерпретации биологических и социальных явлений. Совершенно неожиданно выяснилось, что предыстория может играть роль и в простых химических процессах.
Рассмотрим бифуркационную диаграмму, изображенную на рис. 2.15. От предыдущей диаграммы она отличается тем, что в точке бифуркации появляются два устойчивых решения. В связи с этим, естественно, возникает вопрос: по какому пути пойдет дальнейшее развитие системы после того, как мы достигнем точки бифуркации? У системы имеется «выбор» : она может отдать предпочтение одной из двух возможностей, соответствующим двум неравномерным распределениям концентрации Х в пространстве (рис. 2.16).
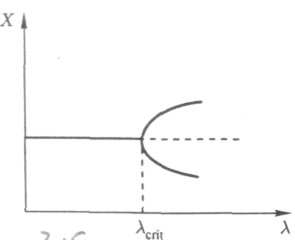
Рис. 2.15. – Симметричная бифуркационная диаграмма. Х как функция параметра бифуркации l. При l ≤ lcrit , существует только одно стационарное состояние, которое устойчиво. При l ³ lcrit существует два стационарных состояния при любом значении l (прежнее устойчивое стационарное состояние теряет устойчивость).
Каждое из этих распределений зеркально симметрично другому: на рис. 2.16 (а) концентрация Х больше справа, на рис. 2.16 (б) - слева. Каким образом система выбирает между правым и левым? В этом выборе неизбежно присутствует элемент случайности: макроскопическое уравнение не в состоянии предсказать, по какой траектории пойдет эволюция системы. Не помогает и обращение к микроскопическому описанию. Не существует также различия между правым и левым. Перед нами – случайные явления, аналогичные исходу бросания игральной кости.
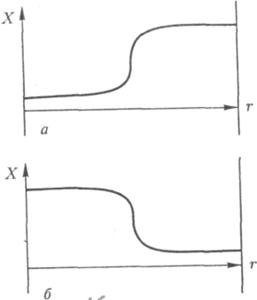
Рис. 2.16. – Два возможных пространственных распределения концентрации компоненты Х, соответствующие двум ветвям на бифуркационной диаграмме (рис. 5.9): (а)отвечает «правой» структуре; концентрация Х в правой части выше, чем в левой; (б) отвечает «левой» структуре (r – парметр бифуркации).
Можно было бы ожидать, что при многократном повторении эксперимента при переходе через точку бифуркации система в среднем в половине случаев окажется в состоянии с максимумом концентрации справа, а в половине случаев – в состоянии с максимумом концентрации слева.
Однако, у некоторых биологических объектов возникает так называемая дисимметрия. Например, направление закрутки раковин. У большинства особей закрутка развита преимущественно в одну сторону.
Таким образом, дисимметрия обусловлена единичным событием, случайным образом отдавшим предпочтение одному из двух возможных исходов. После того как выбор произведен, в дело вступает автокаталитический процесс и левосторонняя структура порождает новые левосторонние структуры. Другой ответ предполагает «войну» между лево- и правосторнними структурами, в результате которой одни структуры уничтожают другие.
К сожалению удовлетворительным ответом на этот вопрос современная наука не располагает.
Однако, следует сделать важный вывод, что бифуркации по времени могут определяться не изменением параметров, а ходом процессов самоструктурализации данной среды. Наконец, могут происходить изменения (вынужденные или спонтанные) самой открытой нелинейной среды. А если среда становится другой, то это приводит к качественному изменению картины процессов ее эволюции. На более глубинном уровне происходит переделка, перестктурализация поля возможных путей эволюции среды.
Резкое изменение направления развития в точке бифуркации, когда система скачком переходит в новое состояние (т.е. жесткие бифуркации) характерны для революционных процессов. Хотя, как было отмечено ранее, разница между эволюционным и революционным событием – лишь в скорости течения процесса.
Типичные признаки бифуркации:
· чувствительность к малым воздействиям вблизи точки бифуркации, т.е. система становится предельно уязвимой;
· неустойчивость предшествующего состояния;
· возможность катастрофических скачков – конечного отклика на бесконечно малые воздействия.
| <== предыдущая страница | | | следующая страница ==> |
| Причины прогрессивной эволюции | | |
Дата добавления: 2014-05-02; просмотров: 382; Нарушение авторских прав

Мы поможем в написании ваших работ!