
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Лекция 8. Реологические свойства характеризуют изменение всех механических свойств пласта при воздействии нагрузок
Реологические свойства характеризуют изменение всех механических свойств пласта при воздействии нагрузок.
Поведение пластов при длительном и кратковременном нагружении различно: при кратковременном нагружении происходит разрушение, длительная же нагрузка приводит к проявлению пластических свойств на известняках (образуются складки).
 |
К пластическим относятся следующие свойства:
& явление ползучести, или крипа
Крип – явление постепенного роста деформации при постоянном нагружении.
Для корунда график зависимости выглядит следующим образом:






 e
e
5%
I II III
400 ч t
Если корунд нагреть до температуры t°=1300°, он начнёт ползти по такой кривой.
При меньших значениях температур происходит ползучесть кварца, кальцита, доломита и других минералов.
Для нефтегазового пласта явление ползучести связано с переползанием отдельных дислокаций перпендикулярно плоскости скольжения.
Важную роль также играет и вязкостное сопротивление.
Кривая ползучести состоит из трёх областей:
I. обычный рост мгновенных деформаций;
II. установившееся течение при постоянной нагрузке;
III. стадия нарастания скорости деформации до наступления момента разрушения породы.
Механизм разрушения в случае пластической деформации отличен от хрупко-пластического.
Т.о. для феноменологического описания явления ползучести применяется вязкоупругая модель Максвелла.
До предела упругости общая деформация составляет:
ee=eЕ+eп
где eп – пластическая деформация, eЕ – упругая деформация.
Эта деформация меняется во времени:
dee/dt=deЕ/dt+deп/dt
eЕ=s/Е Þ deп/dt=1/Е×(j(s, t))
dee/dt=1/Е×(ds/dt+j(s, t)) - уравнение ползучести
В случае s=соnst dee/dt=1/Е×(j(s, t))
Отсюда можно сделать вывод, что деформация ползучести зависит от предыстории нагружения. Это явление называется наследственностью.
Согласно теории наследственности, если в момент времени s(t) действует напряжение dt, то j(s, t) может быть представлена в виде:
j(s, t)=s(t)×L(t - t),
где L(t - t) – ядро ползучести.
Ядра ползучести определяются в условиях лабораторного эксперимента, по данным эксперимента предлагаются различные виды функций:
L(t-t)=d(t-t)-a d>0, a>0
L(t-t)=а×е-в×(t-t)
Ползучесть присуща таким породам, как глина, аргиллит, глинистые сланцы, соли и т.д.
Ползучесть зависит от нагрузки на породу и направлении приложения нагрузки.
Максимальная ползучесть наблюдается в направлении перпендикулярном слоям. Отношение ползучести перпендикулярной слою к ползучести, направленной параллельно, достигает значения 1.4.
 |
& Другое свойство, обратное ползучести, - релаксация напряжений.
Она представляет собой ползучесть при напряжении, которое уменьшается пропорционально нарастающей пластической деформации.
При её изучении мы также фиксируем напряжения.
Т.о. релаксация и ползучесть – явления одного свойства.
Напряжения, которые возникают в первые моменты, при релаксации характеризуются упругой деформацией, которая переходит в пластическую.
de/dt=0 Þ
ds/dt=-s(t)×L(t-t) - уравнение релаксации
Оно следует из общего уравнения ползучести, при условии, что деформация постоянна.
Установлено, что: s=s0×е-t/t0,
где t0 – время, в течение которого напряжение s0 убывает в е раз, и это время называется периодом релаксации.
Период релаксации для большинства пород величина большая (~100-1000 ч), поэтому чаще на практике используется величина относительного падения напряжений R¢.
R¢=(s1-s2)/s1×100,
где s1 – напряжение в момент времени t1;
s2 – напряжение в момент времени t2.
Известно, что период релаксации уменьшается с ростом температуры и с ростом первоначального напряжения.
При воздействии длительных напряжений прочностные свойства породы (модуль Юнга (Е) и предел упругости) становятся меньше, т.е. прочность падает. Для характеристики длительных воздействий используют понятие текущей, или длительной, прочности.
s
 |
s0
 |
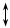
 sдл
sдл
s¥
 t
t
sдл – текущая прочность; s0 – мгновенный предел прочности; s¥ - предел прочности при длительном воздействии.
sдл<s0
Для разных пород связь между sдл и s0 различна:
sдл=s0×1g(В/t),
где В – свойство породы, характеризующее её стойкость к длительному воздействию.
Модуль упругости при длительном воздействии меньше начального (Е0) и составляет:
Е¥=(0.67¼0.95)×Е0
Уменьшение прочности пород при длительном воздействии иногда определяют величиной, называемой коэффициентом расслабления, который равен отношению мгновенного предела прочности к длительному: s0/sдл.
Значения этого коэффициента для некоторых пород приведены в таблице 1:
Таблица 1.
| порода | s0/sдл |
| глина | 1.5 |
| песчаник | 1.8 |
| бетон | 1.67 |

Лекция 8
1. В модели Солоу в долгосрочном периоде с увеличением объема выпуска фирмы капиталоемкость производства K/Y растет, снижается, остается неизменной или поведение этой величины неоднозначно? K – капитальные ресурсы, Y – объем производства.
Ведет себя неоднозначно
Снижается
Растет
Остается неизменной
2. Увеличение какого из управляющих параметров модели Солоу приведет к увеличению темпов экономического роста в долгосрочном периоде?
Необходимо увеличить норму амортизации и норму накопления
Нормы накопления
Нормы амортизации
Темпа прироста числа занятых
3. Рассмотрите модель Солоу с производственной функцией 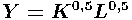 . Пусть норма накопления равна 30 %, темп роста населения равен 1 %, а норма амортизации составляет 2 %. Чему равно в стационарном состоянии подушевое потребление? Ответ должен быть целым числом.
. Пусть норма накопления равна 30 %, темп роста населения равен 1 %, а норма амортизации составляет 2 %. Чему равно в стационарном состоянии подушевое потребление? Ответ должен быть целым числом.
Внимание! Посмотрите, такие ли у вас цифры. Если нет, то найдите ответ самостоятельно по приведенному ниже алгоритму…
Решение: По условию: ν = 0,01; μ = 0,02; ρ = 0,3
Формула для подушевого потребления: 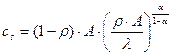 , где
, где 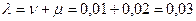
В общем виде производственная функция имеет вид 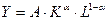
В нашем случае 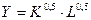 , поэтому
, поэтому 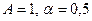
Теперь можем найти решение:
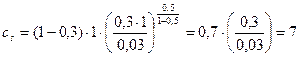
Ответ: 7
4. В рамках модели Солоу рассмотрите две страны (А и Б) с одинаковыми производственными функциями, нормами сбережения, темпами роста населения и темпами амортизации. В настоящий момент времени подушевой капитал страны А превосходит подушевой капитал страны Б. Что можно сказать о темпах роста ВВП в этих странах в ближайшей перспективе?
Решение: Нужно воспользоваться правилом: в стране с меньшим уровнем подушевого капитала – темп больше.
Темп роста капитала в странах А и Б будет одинаков
Темп роста капитала в стране Б будет выше чем в стране А
Темп роста капитала в стране А будет выше чем в стране Б
Темп роста капитала в странах А и Б будет меняться неоднозначно
5. В рамках модели Солоу рассмотрите две страны (А и Б) с одинаковыми производственными функциями, темпами роста населения и темпами амортизации. В стране А норма сбережения выше, чем в стране Б. В какой из стран выше подушевое потребление в долгосрочном периоде?
Однозначно ответить невозможно
Подушевое потребление в странах А и Б одинаково
Подушевое потребление выше в стране Б
Подушевое потребление выше в стране А
6. При каких условиях темп прироста капитала отличается от темпа прироста занятых в экономике в модели Солоу?
Если не реализуется режим "золотого правила накопления"
В стационарном режиме.
Если реализуется режим "золотого правила накопления"
Пока не достигнут стационарный режим.
7. К каким последствиям приведет в модели Солоу рост нормы сбережения в долгосрочной перспективе? НЕВЕРНО!!!
К росту подушевого потребления
К росту подушевого выпуска продукции
К росту подушевых инвестиций
К росту подушевого капитала
К росту подушевого потребления
К росту подушевого выпуска продукции
К росту подушевых инвестиций
К росту подушевого капитала
8. К каким последствиям приведет в модели Солоу в подушевых переменных увеличение темпа прироста населения, занятого в экономике, в долгосрочной перспективе?
Увеличению подушевых инвестиций.
Уменьшению подушевого выпуска продукции
Увеличению подушевого потребления
Уменьшению подушевого капитала
9. Какие величины, согласно модели Солоу без технического прогресса, остаются постоянными в стационарном состоянии, а какие изменяются?
Подушевой капитал k: не изменяется
Число занятых в экономике L: изменяется
Интегральный объем ВВП Y: изменяется
Подушевое потребление: не изменяется
10. Рассмотрите модель Солоу с производственной функцией Y = K0,5 *L0,5. Пусть темп роста населения равен 3 %, а норма амортизации составляет 2 %. Чему равно подушевое потребление, соответствующее «золотому правилу», в долгосрочном периоде? Ответ привести с точностью до целых.
Внимание! Посмотрите, такие ли у вас цифры. Если нет, то найдите ответ самостоятельно по приведенному ниже алгоритму…
Решение: Нам дано: 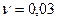 ,
, 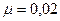 .
.
По золотому правилу 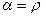 . Из производственной функции ясно, что
. Из производственной функции ясно, что 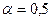 , А = 1. Поэтому,
, А = 1. Поэтому, 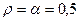 .
.
Ф-ла для подушевого потребления: 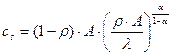 ,
, 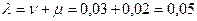
Подставляем данные: 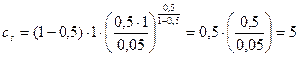
Ответ: 5
11. Рассмотрите модель Солоу с производственной функцией Y=K0,7L0,3. Пусть темп роста населения равен 1,5 %, а норма амортизации составляет 2 %. Чему равны подушевые инвестиции, соответствующее «золотому правилу»?
Ответ привести с точностью двух знаков после запятой, например, так 345,89.
Внимание! Посмотрите, такие ли у вас цифры. Если нет, то найдите ответ самостоятельно по приведенному ниже алгоритму…
Решение: Нам дано: 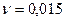 ,
, 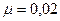 .
.
Из производственной функции находим: 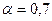 , А = 1
, А = 1
По золотому правилу 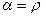 , поэтому
, поэтому 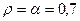
Ф-ла для подушевых инвестиций: 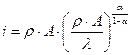 , где
, где 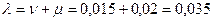
Подставляем значения: 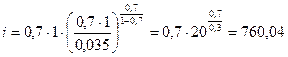
12. Пусть экономика, описываемая моделью Солоу, находилась в стационарном состоянии с подушевым капиталом k1 и подушевым выпуском y1. В результате землетрясения 20 % капитала страны было разрушено, но темп прироста числа занятых в экономике остался неизменным. По истечении некоторого времени экономика достигла нового стационарного состояния с подушевым капиталом k2 и подушевым выпуском y2. Что можно сказать о соотношении величин k1, y1 и k2, y2, если все параметры модели Солоу остались неизменными?
k1 = k2; y1 = y2
| <== предыдущая страница | | | следующая страница ==> |
| Реологические свойства нефтегазовых пластов | | | Методы обработки рукавов в верхней одежде |
Дата добавления: 2014-05-17; просмотров: 307; Нарушение авторских прав

Мы поможем в написании ваших работ!