Однофакторный дисперсионный анализ. Закон Фишера–Снедекора распределения непрерывной случайной величины

Для определения критерия, меры, с помощью которой можно решить вопрос о значимости величины факторной дисперсии, сначала надо рассмотреть факторную и остаточную дисперсии с позиций непрерывной случайной величины.

Если варианты x_ki считать случайными порождениями непрерывных случайных величин X_ki, которые распределены по нормальному закону с математическим ожиданием m_x и средним квадратическим отклонением σ_x, то можно считать, что случайные величины

,

порождающие значения выборочных средних для каждого уровня рассматриваемого фактора

,

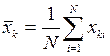будут тоже распределены по нормальному закону с тем же математическим ожиданием m_x, но с другим средним квадратическим отклонением, которое есть .

В связи с этим можно утверждать, что факторная дисперсия в нормированном следующим способом виде

является порождением непрерывной случайной величины

,

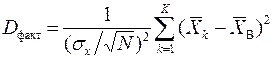которая распределена по закону χ² с (K – 1)-ой степенью свободы.

Аналогичные рассуждения можно выполнить для остаточной дисперсии. Она в нормированном виде

,

является порождением непрерывной случайной величины

,

которая тоже распределена по закону χ², но с (KN – K) степенями свободы.

Теорема. Если U и V – непрерывные случайные величины, распределённые по закону χ² с k_U и с k_V степенями свободы соответственно, то их композиция

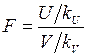
имеет распределение, которое называется F-распределением Фишера–Снедекора, с плотностью

,

где

,

а Г(x) – гамма-функция Гаусса.

Подсчёт вероятности попадания непрерывной случайной величины, подчиняющейся закону Фишера–Снедекора, на заданный интервал от a до b, осуществляется с помощью плотности распределения традиционным образом

.

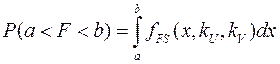Её вычисление в среде Excel’а выполняется с помощью стандартной функции FРАСП(δ; k_U; k_V), которая определяется интегралом

FРАСП(δ; k_U; k_V) ,

где k_U и с k_V – степени свободы закона. Делается это на основе свойства определённого интеграла следующим образом

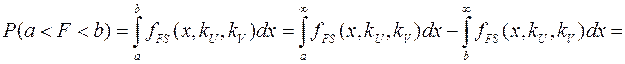
= FРАСП(a; k_U; k_V) – FРАСП(b; k_U; k_V).

Для решения обратной задачи – определения по заданной вероятности границ локализации случайной величины, которая распределена по закону Фишера–Снедекора, в Excel’е существует стандартная функция FРАСПОБР(α; k_U; k_V). С её помощью для заданной вероятности

можно найти левую границу δ полубесконечного интервала локализации величины F

δ = FРАСПОБР(α; k_U; k_V),

где k_U и с k_V, как и ранее, обозначают числа степеней свободы рассматриваемого закона.

В соответствии с рассмотренной теоремой случайные величины D_факт и D_ост порождают случайную величину

,

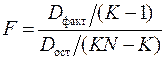которая распределена по закону Фишера–Снедекора с (K – 1)-ой и (KN – K)-ой степенями свободы, и которая может быть использована для решения вопроса о значимости величины факторной дисперсии.

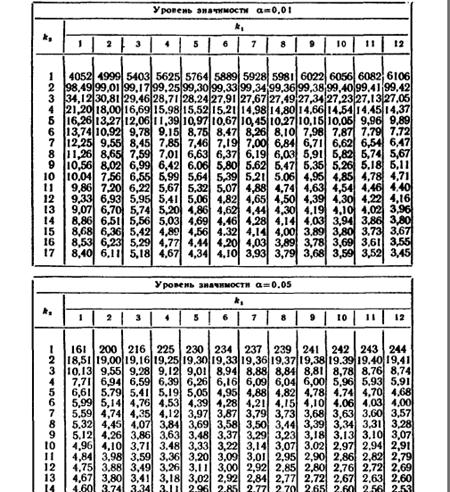
Таблицу распределения Фишера можно найти практически в каждой книге по математической статистике, в частности в Приложении №7 книги Гмурмана В.Е. Теория вероятностей и математическая статистика.

Дата добавления: 2014-06-19; просмотров: 1736; Нарушение авторских прав

Мы поможем в написании ваших работ!