
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Однофакторный дисперсионный анализ. Предварительные расчеты
[1] Сюкияйнен Л. Р. Доктрина как источник мусульманского права.//Источники права. – М., 1985. – C. 65-83.
[2] Бабаев В. К. Общая теория права. Курс лекций. – Н. Новгород, 1993. – С. 251.
[3] Социалистическое право / Айзенберг А. М., Александров Н.Г., Алексеев С.С., Лукашева Е. А., и др. – М .: Юрид. лит., 1973. – С.325.
[4] Ображиев К. Судебный прецедент в уголовном праве России // Уголовное право. 2004. № 3. – С. 58.
[5] Консультации по теории государства и права: учебн. пособие/ Н. А. Пьянов. – Изд. 2-е, перераб. и доп. – Иркутск: Изд-во Ирк. гос. ун-та, 2008. – С. 181.
Однофакторный дисперсионный анализ. Предварительные расчеты
Пусть для параметра x системы выполнено N опытов для каждого из K уровней проверяемого фактора A. Эти данные, представляющие собой случайную выборку, приведены в таблице ниже
| № опыта | Уровни фактора A | ||||
| A1 | A2 | A3 | … | AK | |
| x11 | x21 | x31 | … | xK1 | |
| x12 | x22 | x32 | … | xK2 | |
| x13 | x23 | x33 | … | xK3 | |
| … | … | … | … | … | … |
| N | x1N | x2N | x3N | … | xKN |
Для этих данных, которые считаются распределёнными по нормальному закону, можно вычислить выборочную среднюю, выборочную дисперсию и выборочное среднее квадратическое отклонение
 .
.
Известно, что выборочная дисперсия dв показывает степень разброса значений xki измеряемого параметра x около его среднего значения, определяемого величиной выборочной средней 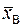 . Этот разброс рассматриваемого параметра x определяется случайными влияниями на него всех факторов рассматриваемой системы, в том числе и проверяемого фактора A. Поэтому процесс формирования случайных значений параметра x можно представить в следующем виде
. Этот разброс рассматриваемого параметра x определяется случайными влияниями на него всех факторов рассматриваемой системы, в том числе и проверяемого фактора A. Поэтому процесс формирования случайных значений параметра x можно представить в следующем виде
 ,
,
где αk – случайное влияние уровня Ak фактора A, а εki – неконтролируемые в данных опытах случайные независимые воздействия остальных факторов. Тогда выборочная дисперсия рассматриваемой выборки может быть представлена так, как это показано ниже


 .
.
Было замечено, что она может быть разделена на факторную дисперсию dфакт, которая определяется случайными отклонениями αk фактора A, и остаточную дисперсию dост, которая определяется неконтролируемыми случайными воздействиями εki остальных факторов
 .
.
Их следует вводить следующим образом
 ,
,
где  обозначают выборочные средние для каждого уровня рассматриваемого фактора
обозначают выборочные средние для каждого уровня рассматриваемого фактора
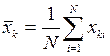 .
.
Покажем это. Для этого сначала следует записать выборочные средние для каждого уровня рассматриваемого фактора через αi и εik
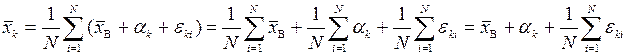 .
.
Далее это же надо сделать для факторной и остаточной дисперсий
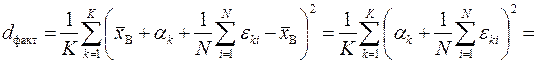
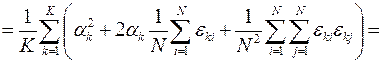
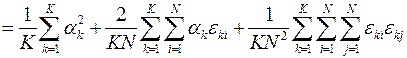 ,
,
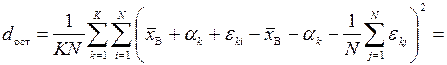
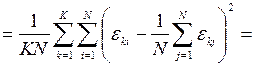

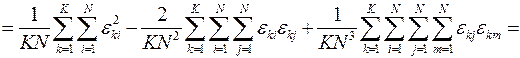

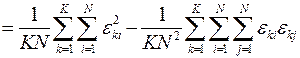 .
.
Из полученных соотношений видно, что факторная дисперсия в основном определяется случайными воздействиями αk фактора A, а остаточная дисперсия определяется только неконтролируемыми случайными воздействиями εki остальных факторов. При этом сумма факторной и остаточной дисперсий равна выборочной дисперсии всей выборки


 .
.
Замечание. Обычно остаточную дисперсию рассчитывают не непосредственно, а через общую дисперсию и факторную дисперсию
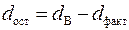 .
.
Факторная и остаточная дисперсии используются для решения вопроса о существенности или несущественности влияния изучаемого фактора на рассматриваемый параметр системы. Если выясняется, что факторная дисперсия невелика по отношению к остаточной дисперсии, то считается, что фактор A не оказывает существенного влияния на параметр x, в противном случае он значим и его можно использовать для совершенствования системы. Остаётся найти меру, грань, которая делит интервал значений факторной дисперсии на интервалы, в одном из которых фактор A следует признать значимым, а в другом – несущественным.
| <== предыдущая страница | | | следующая страница ==> |
| Нормативный правовой акт | | | Однофакторный дисперсионный анализ. Закон Фишера–Снедекора распределения непрерывной случайной величины |
Дата добавления: 2014-06-19; просмотров: 478; Нарушение авторских прав

Мы поможем в написании ваших работ!