ДИСПЕРСИОННЫЙ АНАЛИЗ

Дисперсионный анализ нами будет рассматриваться в несколько упрощенном виде - в качестве вспомогательного средства при проведении корреляционного и регрессионного анализа. Задачей дисперсионного анализа в данном контексте является изучение влияния одного или нескольких предикторов (в том числе и качественных) на предиктант. Основным положением является положение о том, что общая дисперсия предиктанта представима в виде суммы двух дисперсий: «объясненной» влиянием предикторов и «необъясненой» дисперсией - дисперсией, связанной с влиянием неучтенных величин.

Сопоставляя дисперсии, можно установить степень влияния величины Х ( или нескольких величин) на величину Y по сравнению с влиянием неучтенных случайных величин.

В зависимости от числа признаков, чье влияние на предиктант исследуется с помощью дисперсионного анализа, различают однофакторный, двухфакторный и многофакторный дисперсионный анализ.

Простым примером дисперсионного анализа может являться проверка качества уравнения регрессии с помощью квадрата множественного коэффициента корреляции. При этом средняя ошибка регрессии вычисляется таким образом:

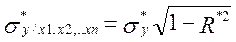, (17)

где s_y/x1,...,xn - средняя квадратическая ошибка регрессии;

s_y - среднее квадратическое отклонение предиктанта;

R^*2 - квадрат множественного коэффициента корреляции (коэффициент детерминации).

Коэффициент детерминации представляет собой долю дисперсии предиктанта, обусловленную влиянием предикторов. Разумеется, чем выше его значение, тем более качественным является уравнение регрессии.

Дата добавления: 2014-08-04; просмотров: 307; Нарушение авторских прав

Мы поможем в написании ваших работ!