КОРРЕЛЯЦИОННЫЙ АНАЛИЗ

Разработка прогностических методик, по сути, сводится к задаче установления связи между метеорологическими величинами. Как и любые случайные величины, метеовеличины могут быть связаны между собой либо функциональной либо статистической связью, а могут быть и не связаны между собой.

Наиболее характерной является статистическая связь метеорологических величин. Она характеризуется тем, что каждому значению одной величины соответствует одно и только одно распределение значений другой величины. С изменением одной величины изменяется закон распределения другой.

Задачамикорреляционного анализа являются:

- измерение степени взаимной зависимости двух и более величин;

- отбор величин, оказывающих наиболее существенное влияние на результативный признак, на основании измерения степени связи между метеорологическими величинами;

- обнаружение ранее неизвестных связей между величинами.

Рассмотрим практические приемы оценивания показателей тесноты связи по выборочным данным.

Одним из показателей тесноты линейной связи между переменными являетсякорреляционный момент. Корреляционный момент (ковариация) двух случайных величин X и Y - это математическое ожидание произведения соответствующих центрированных случайных величин:

о o

K_xy = M[X Y]. (1)

Формула для вычисления корреляционного момента между дискретными случайными величинами имеет вид:

_{n m}

K_xy = S S (x_i - m_x)(y_j - m_y) p_ij. (2)

^{i=1 j=1}

На практике для определения значения K_xy по результатам наблюдений за случайными величинами используются формулы:

_n

K_xy = (1/n) S (x_i - m_x*)(y_j - m_y*). (3)

ⁱ⁼¹

_n

или K_xy = (1/n) S x_i y_j - m_x* m_y*. (4)

ⁱ⁼¹

Для получения несмещенной оценки корреляционного момента следует использовать формулу:

_n

K_xy = (1/n-1) S x_i y_j - (n/n-1) m_x* m_y*. (5)

ⁱ⁼¹

Во всех выражениях n - число сопряженных во времени или пространстве наблюдений над X и Y.

Корреляционный момент K_xy характеризует одновременно и линейную зависимость случайных величин и их рассеяние около центра распределения (m_x, m_y). Поэтому его трудно использовать непосредственно для оценивания степени связи случайных величин. Для характеристики только теснотылинейной связи двух или нескольких случайных величин используется безразмерные величины -коэффициенты корреляции.

Различаютпарный, частный и множественный коэффициенты корреляции. (Следует заметить, что данный перечень не включаетбисериальный коэффициент корреляции, характеризующий связь количественной случайной величины с дихотомической).

Парный коэффициент корреляции r_xy характеризует тесноту линейной статистической связи между двумя случайными величинами X и Y. Оценка его вычисляется для выборочных данных следующим образом:

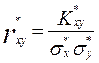, (6)

где К^*_xy - оценка корреляционного момента (выборочное значение);

s^*_x и s^*_y - оценки средних квадратических отклонений X и Y.

Парный (как и любой другой) коэффициент корреляции может принимать значения от -1 до 1, т.е.: -1 £ r_xy £ 1.

Случайные величины, корреляционный момент и коэффициент корреляции между которыми не равны нулю, называютсякоррелированными. Если r_xy > 0, то такая корреляция называется положительной, а если r_xy < 0, то - отрицательной.

Положительная корреляция означает, что при возрастании одной случайной величины другая имеет тенденцию к возрастанию. Отрицательная корреляция означает, что при возрастании одной случайной величины другая имеет тенденцию к убыванию.

Выборочное значение коэффициента корреляции является приближенной оценкой его истинного значения. Поэтому для получения правильного представления о тесноте линейной связи между анализируемыми величинами следует проверить точность и значимость полученной оценки коэффициента корреляции. Для проверки значимости выдвигается нулевая гипотеза, заключающаяся в том, что коэффициент корреляции равен нулю. Чтобы проверить данную гипотезу используется показатель согласованности следующего вида:

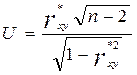(7)

подчиняющийся закону распределения Стьюдента с (n-2) степенями свободы.

Проверка состоит в следующем:

- по заданному уровню значимости a и числу степеней свободы (n-2) по таблице распределения Стьюдента определяется критическое значение показателя согласованности U_кр;

- вычисляется значение U по формуле (7);

- если ½U½ < U_кр то нулевая гипотеза принимается, в противном случае оценка коэффициента корреляции признается значимой.

Средняя ошибка оценки парного коэффициента корреляции может быть приближенно определена по формуле:

s 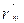= 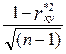. (8)

Парные коэффициенты корреляции опосредованно учитывают влияние других факторов и поэтому не всегда отражают действительную связь между рассматриваемыми случайными величинами. Для исключения влияния других величин определяют частные коэффициенты корреляции.

Частный коэффициент корреляции между случайными величинами X и Y при фиксированном значении случайной величины Z определяется как:

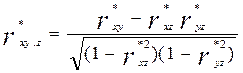. (9)

Если условие постоянства накладывается на две случайные величины выражение для определения частного коэффициента корреляции несколько усложняется. К примеру, частный коэффициент корреляции между случайными величинами Y и X₁ при фиксированных значениях случайных величин X₂ и X₃ определяется как:

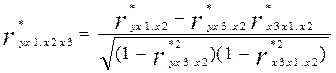. (10)

Последовательность и содержание проверки значимости полученных оценок частного коэффициента корреляции почти не отличаются от описанных выше. Единственным отличием является то, что число степеней свободы (см. (7)) равно (n-3), а не (n-2).

Средняя ошибка оценки частного коэффициента корреляции может быть приближенно определена по формуле:

s 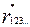= . (11)

где m - число независимых переменных в рассматриваемой многомерной связи.

Множественный коэффициент корреляции характеризует многостороннюю связь одной случайной величины с несколькими другими. Выражение для определения множественного коэффициента корреляции Y с X₁ и X₂ имеет вид (выражение (12)):

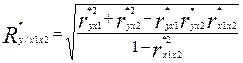. (12)

Если анализируется связь между большим числом случайных величин, то выражение для расчета множественного коэффициента корреляции сильно усложняется. В этом случае его можно вычислить по формуле:

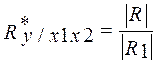, (13)

где | R | - определитель матрицы парных коэффициентов корреляции (корреляционной матрицы);

| R₁| - определитель матрицы, образованной из корреляционной матрицы путем вычеркивания элементов первой строки и первого столбца.

Проверка значимости множественного коэффициента корреляции проводится в описанной выше последовательности. При этом в качестве показателя согласованности используется показатель вида

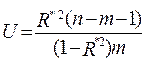, (14)

где m - число независимых переменных в рассматриваемой многомерной связи.

Средняя ошибка оценки множественного коэффициента корреляции может быть приближенно определена по формуле:

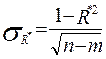, (15)

Следует заметить, что равенство нулю любого коэффициента корреляции не означает независимость исследуемых величин, а лишь указывает на отсутствие линейной связи между ними (кроме линейной возможно существование иной формы зависимости между переменными).

Итак, значения коэффициентов корреляции позволяют оценить степень линейной связи между различными величинами. Зависимость между случайными величинами часто представляется в видеуравнения регрессии. К примеру, линейное уравнение множественной регрессии имеет вид:

y = a_o + a₁x₁ + ... + a_mx_m, (16)

где y - предиктант;

a_o, ..., a_m - коэффициенты уравнения регрессии;

x₁, ..., x_m - предикторы.

Дата добавления: 2014-08-04; просмотров: 433; Нарушение авторских прав

Мы поможем в написании ваших работ!