
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Оценка точности и достоверности результатов выборочного наблюдения
I. Статистическая сводка, ее задачи и роль в статистическом исследовании.
В результате статистического наблюдения получают информацию, представленную огромным количеством первичных сведений, отраженных в статистических карточках, учетных журналах и других документах.
Все эти сведения характеризуют лишь отдельные единицы исследуемой совокупности (пол, возраст, образование). С помощью разрозненных сведений нельзя сделать выводы об объекте исследования в целом.
Для того, чтобы дать сводную характеристику экономическим, социальным, правовым значимым явлениям и процессам, необходимо привести материалы статистического наблюдения (разнообразные данные об отдельных правонарушениях) в определенный порядок, систематизировать, что достигается на 2 этапе статистического исследования, называемом статистической сводкой.
Статистическая сводка представляет собой научную обработку материалов статистического наблюдения, включающую в себя систематизацию и группировку первичных статистических сведений, внесение их в таблицы, подсчет групповых и общих итогов, расчет производных показателей для характеристики групп и объекта в целом (средних, относительных величин).
Роль сводки в статистическом исследовании возрастает в условиях рыночной экономики, поскольку и итоговые данные по основным показателям могут быть получены быстро и служить основой для принятия оперативных управленческих решений, связанных со сложившейся по конкретным товарам конъюнктурой рынка.
Задача сводки - дать характеристику объекту исследования с помощью запроектированных систем статистических показателей, выявить и измерить такие путем его существенные черты и особенности.
Статистическая сводка, должна проводиться по определенной программе, которая составляется еще до сбора статистических данных.
Программа включает определение:
- задачи сводки на основе целей статистического исследования;
-групп и подгрупп;
-системы показателей
-видов таблиц,
а также содержит информацию о последовательности и сроках выполнения отдельных этапов сводки, ее исполнителях и порядке представления результатов.
По сложности представления информации различают:
1) простую сводку, когда итоги подсчитывают сразу по всей совокупности;
2) сложную сводку, когда единицы совокупности предварительно группируют по какому-либо признаку и подсчитывают итоги вначале по группам, а затем за всю совокупность.
Например:
| Группы квартир по форме собственности | Число квартир | Число жильцов, чел. | |
| Муниципальная | |||
| Частная | |||
| Итого | |||
Проведение статистической сводки позволяет упорядочить разрозненную информацию об отдельных единицах совокупности и перейти к характеристике всей совокупности или отдельных групп ее единиц. Например, данная сводка позволяет выделить два типа квартир по форме собственности и сделать вывод о преобладании частных квартир над муниципальными как по их числу, так и по числу проживающих в них людей.
По форме обработки материала сводка бывает:
1) централизованная (первичные данные обрабатываются в центральном органе, например Росстате, ГИЦ МВД России).
2) децентрализованной (документы первичного учета обобщаются сводятся на местах, и в вышестоящий орган направляются уже в окончательном варианте).
3) смешанной (обработка первичного материала осуществляется частично на местах и завершается полностью в вышестоящий орган).
По способу выполнения сводка может быть ручной или автоматизированной, то есть выполняемой с помощью ЭВМ.
2.Группировка как научная основа сводки и метод исследования. Виды группировок. Ряды распределения, расчет соответствующих показателей.
В основе сводки любого статистического материала всегда лежит группировка (объединение групп) отдельных единиц совокупности.
Статистическая группировка - это процесс разделения статистической совокупности на качественно однородные группы или объединение единичных случаев в качественно однородные группы по существенным для них признакам.
Например, группировка преступлений по видам, категориям тяжести, способам совершения.
Отбор существенных (группировочных) признаков определяется целям и задачам исследования и заключается в разделении единиц статистической совокупности на однородные группы по существенным для них признакам.
В зависимости от цели и задач исследования статистические группировки бывают:
1) типологическая - для выделения качественных типов внутри явления. Например, представленная выше группировка квартир жилого дома по форме собственности;
2) структурная - для изучения структуры явления и характеризующих его признаков в зависимости от группировочного признака.
Например:
Группировка населения РФ по размеру среднедушевого дохода (условные цифры)
| Группировка № п/п | Среднедушевой денежный доход, тыс. руб. в месяц | Численность населения | |
| всего, млн. человек | в % к итогу | ||
| 1. 2. 3. 4. 5. 6. 7. 8. | До 10000 10000–15000 15000–17000 17000–20000 20000–30000 30000–35000 35000–50000 50000 и более | 3,4 22,4 34,5 28,7 21,6 12,6 9,8 15,4 | 2,3 15,2 23,3 19,4 14,6 8,3 6,6 10,3 |
3) аналитическая - для выявления связей между признаками, характеризующими явление.
Например:
Группировка продолжительности договорных связей книжного магазина и качества продукции
| Продолжительность договорных связей магазина с поставщиками, лет | Число поставщиков | Доля качественной стандартной книжной продукции, % | |
| Абсолютное | в % к итогу | ||
| До 2 | |||
| 3–5 | |||
| 5–8 | |||
| Свыше 8 | |||
| Итого | 74,8 |
Такая группировка позволяет проанализировать зависимость доли качественной книжной продукции от продолжительности договорных связей магазина с поставщиками.
Группировка по одному признаку называется простой, по двум и более – сложной. Сложные группировки бывают комбинационными и многомерными.
При комбинационной группировке группы, образованные по одному признаку, делят на подгруппы по второму признаку и т. д. Итоги при этом подсчитывают в обратном порядке.
При многомерной группировке единицы группируются одновременно по нескольким признакам. В общем случае такие группировки не могут быть созданы в ручную и формируются только с использованием ЭВМ.
Особенности построения количественных группировок
Если группировочный признак является дискретным и число его вариантов невелико, то единицы разбиваются на группы по этим вариантам. Например, группы рабочих по вариантам тарифного разряда.
Если число вариантов велико, то их объединяют в интервалы. Также поступают, если признак является непрерывным, то есть принимает любые значения в заданных пределах.
При этом выполняют два требования:
1) чем больше число единиц и чем сильнее вариация признака, тем больше число интервалов (и наоборот);
2) чем больше число интервалов, тем меньше их величины (и наоборот).
Выполнение требований обеспечивает попадание в каждый интервал достаточного числа единиц и повышает достоверность исследования.
При большом числе единиц (N > 30) число интервалов определяют по формуле Стерджесса:
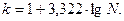
Интервалы могут быть равными и неравными. Равные интервалы применяют при незначительной вариации признака. Их ширину рассчитывают по формуле:
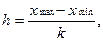
где xmax и xmin – наибольшее и наименьшее значения признака.
Если закон распределения единиц совокупности по величине признака является нормальным, то полагают, что:
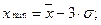
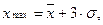
где 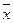 – среднее значение признака;
– среднее значение признака; 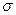 – его среднеквадратическое отклонение.
– его среднеквадратическое отклонение.
Тогда:
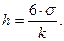
Например, если известно, что для 1000 предприятий среднее число занятых составляет 300 чел. при среднеквадратическом отклонении 11 чел., то число интервалов и их ширину для группировки предприятий по числу занятых определяют следующим образом:

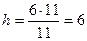 чел.
чел.
Тогда:
xmin = 300 – 3 ∙ 11 = 267 чел.
В результате получаем следующие интервалы: 267 – 273; 273 – 279; ... ; 327 – 333 чел.
Если вариация признака значительна, то используют неравные интервалы, изменяющиеся в арифметической или геометрической прогрессии.
При арифметической прогрессии:
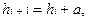
где 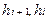 – величина (i+1)-го и i-го интервалов соответственно; a – const. При а > 0 интервалы возрастают, при a < 0 – убывают.
– величина (i+1)-го и i-го интервалов соответственно; a – const. При а > 0 интервалы возрастают, при a < 0 – убывают.
При геометричекой прогрессии:
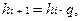
где q – положительная const. При q >1 интервалы возрастают, при q < 1 - убывают.
Границы интервалов могут быть закрытыми, как в рассмотренной группировках, и открытыми, например, «до 100 чел.» или «801 чел. и более». Ширину открытых интервалов определяют исходя из общей тенденции.
Вторичная группировка
При сравнении группировок, отличающихся числом и размером интервалов, их приводят к сопоставимому виду. Для этого за основу берут интервалы одной из группировок, а для другой проводят вторичную группировку.
Если вновь установленный интервал включает в себя какой-либо из старых, то за ним закрепляют все единицы из старого интервала. Если он включает в себя часть старого интервала, то за ним закрепляют долю единиц пропорционально включаемой части.
Понятие ряда распределения
Рядом распределения называется ряд цифровых показателей, представляющих распределение единиц совокупности по одному существенному признаку, разновидности которого расположены в определенной последовательности. В зависимости от вида группировочного признака различают:
1) атрибутивные ряды, когда признак является атрибутивным;
2) вариационные ряды, когда признак является количественным.
В структуре вариационного ряда выделяют:
1) варианты – отдельные значения или интервалы значений признака;
2) частоты – числа, показывающие, сколько раз встречается тот или иной вариант.
В зависимости от формы представления вариантов различают:
1) дискретные вариационные ряды, когда признак принимает только дискретные значения;
2) интервальные вариационные ряды, когда признак является непрерывным и его значения разбивают на интервалы.
Если число вариантов дискретного признака велико, то их группируют, также как и значения непрерывного признака.
Примеры представлены на слайдах.
Показатели структуры ряда распределения
Для характеристики структуры вариационных рядов рассчитывают специальные структурные показатели – моду и медиану.
Мода (Мо) – это значение признака, наиболее часто встречающееся в ряду.
Медиана (Ме) делит ряд таким образом, что одна половина единиц ряда имеет значения признака не более, чем медиана, а другая – не менее.
В дискретном ряду мода равна значению варианта с наибольшей частотой, а медиана – значению первого варианта, для которого накопленная частота превышает половину суммы всех частот. Накопленная частота получается путем суммирования частоты рассматриваемого варианта и частот всех предшествующих вариантов.
В интервальном ряду вначале определяют интервалы, в которых находятся структурные показатели.
При равных интервалах модальный интервал определяется на основе значений частот, также как для дискретного ряда.
При неравных интервалах от частот переходят к плотностям распределения, используя формулу:
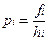 ,
,
где 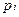 - плотность распределения i-го интервала;
- плотность распределения i-го интервала;
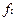 ,
, 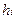 - его частота и ширина.
- его частота и ширина.
Модальным является интервал с максимальным значением 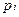 .
.
Медианный интервал определяют аналогично дискретному ряду, независимо от ширины интервалов.
Для определения конкретных значений структурных показателей внутри соответствующих интервалов используют следующие формулы.
Мода:
при равных интервалах
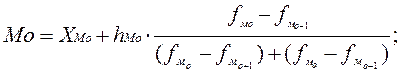
при неравных интервалах
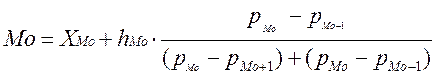 ,
,
где XМо, hМо, fМо, pМо – начало модального интервала, его ширина, частота и плотность распределения;
fМо-1, fМо+1 – частоты интервалов, расположенных перед модальным интервалом и после него соответственно;
pМо-1, pМо+1 – соответствующие им плотности распределения.
Медиана:
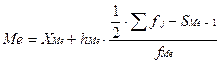 ,
,
где XМе – начало медианного интервала;
hМе, fМе – его ширина и частота;
fj – частота каждого j-го интервала;
SМе-1 – накопленная частота интервала перед медианным интервалом.
3.Понятие статистической таблицы и графика, их виды.
Для наглядности и компактности результаты статистической сводки представляют в виде статистических таблиц и графиков.
Статистические таблицы отличаются от прочих таблиц тем, что представленные в них данные всегда получены на основе статистического наблюдения и статистической сводки.
Например, опросный лист в табличной форме не является статистической таблицей. Занесенная в него информация хоть и получена в результате статистического наблюдения, но никак не сгруппирована и не обобщена.
По логическому содержанию статистическая таблица представляет собой статистическое предложение, состоящее из подлежащего и сказуемого.
Подлежащим таблицы является объект статистического исследования, характеризующийся табличными цифрами. Подлежащее раскрывается в наименовании строк.
Сказуемое – это показатели, которыми характеризуется подлежащее. Сказуемое располагают в наименовании граф.
В зависимости от структуры подлежащего различают:
1) простые таблицы, когда подлежащее содержит простой перечень единиц изучаемого объекта;
2) сложные таблицы, когда единицы объекта сгруппированы по одному или нескольким признакам.
Сложные таблицы делятся на:
1) групповые, когда единицы сгруппированы по одному признаку;
2) комбинационные, когда единицы сгруппированы последовательно по двум и более признакам.
В зависимости от структуры сказуемого различают таблицы:
1) с простой разработкой сказуемого, когда образующие его показатели не подразделяются на составляющие и рассматриваются отдельно;
2) со сложной разработкой сказуемого, когда в составе одного показателя выделяют по какому-либо признаку два и более других показателя.
При построении статистических таблиц необходимо учитывать следующие основные требования:
-если названия граф содержат повторяющиеся термины или имеют общий смысл, то им присваивают общий объединяющий заголовок;
-информация в строках и графах предваряется или завершается итоговыми строками и графами (там, где это имеет смысл). При этом используют словосочетание «В том числе» и слова «Итого» или «Всего»;
-при большом числе граф или строк их следует нумеровать. Графы с названиями строк - прописными буквами латинского алфавита А, В, С и т. д., а все последующие графы и все строки – арабскими цифрами;
-числа располагают в середине графы одно под другим, соблюдая при этом положение запятой и разрядность;
-по возможности числа следует округлять, причем, с одинаковой точностью в пределах одной и той же графы или строки. Отсутствующие знаки после запятой дополняются нулями. Если число меньше принятой точности, то его изображают дробным числом « 0.0 », « 0.00 » и т. д.;
-отсутствие данных в таблице отмечают: знаком « – », если в них нет необходимости; знаком « х », если они не имеют экономического смысла; обозначениями « . . . » или «Нет сведений», если данные по какой-либо причине отсутствуют.
По данным статистических таблиц строят статистические графики. Они позволяют дать более наглядное и полное представление об изучаемом явлении.
Статистический график представляет собой чертеж, на котором статистическая совокупность характеризуется определенными показателями с помощью условных графических образов.
Элементами статистического графика являются:
1) графический образ - точки, линии или фигуры, с помощью которых изображаются статистические величины;
2) система координат - прямоугольная или полярная;
3) масштабная шкала или масштаб;
4) словесное описание графика – его название, подписи вдоль шкал, пояснения к отдельным частям.
По способу построения различают два вида графиков – статистические карты и статистические диаграммы.
Статистические карты используют для изображения распределения статистических величин по поверхности. При этом поверхностью является географическая карта, а средствами изображения – штриховка или фоновая раскраска.
Например, чтобы изобразить данные о плотности населения районов Ленинградской области, необходимо на географической карте заштриховать эти районы. Вид штриховки выбирают в соответствии с интервалом, в котором находится плотность населения района.
Статистические диаграммы используют для сопоставления независимых величин в пространственном, временном или ином аспекте.
В зависимости от решаемых задач статистические диаграммы делятся на диаграммы распределения, сравнения, динамики и структурные диаграммы.
Диаграммы распределения используют для изображения вариационных рядов. К ним относят гистограмму, полигон частот, кумулятивную кривую и огиву. Из диаграмм сравнения чаще всего используют столбиковые, полосовые и квадратные диаграммы.
Столбики могут быть расположены на одинаковом расстоянии, вплотную или с частичным наложением.
Если в столбиковой диаграмме оси координат поменять местами, то получится полосовая диаграмма.
В квадратных диаграммах сравниваемые величины изображают при помощи квадратов. Их площадь пропорциональна этим величинам.
Для изображения изменения статистических величин во времени используют диаграммы динамики, чаще всего – линейные и радиальные.
На одной диаграмме может быть несколько кривых. Так поступают для сравнения динамики различных показателей или одного и того же показателя, но для разных явлений. Например, для сравнения динамики производства легковых и грузовых автомобилей в отдельности.
Для изображения сезонных колебаний применяют радиальные диаграммы.
Для изображения состава статистических совокупностей через соотношение их частей используют структурные диаграммы, чаще всего - секторные.
Оценка точности и достоверности результатов выборочного наблюдения
Ошибка выборки или ошибка репрезентативности представляет собой разность соответствующих выборочных и генеральных характеристик:
Для средней количественного признака рассчитывается по следующей формуле:
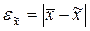 ;
;
где 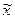 - выборочная средняя,
- выборочная средняя, 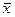 - генеральная средняя
- генеральная средняя
Для доли (альтернативного признака) рассчитывается по следующей формуле:
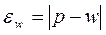
где w – выборочная доля, p - генеральная доля для альтернативного атрибутивного признака.
Ошибка выборки является случайной величиной, так как заранее неизвестно, какие единицы попадут в выборочную совокупность. Поэтому, оценивая точность результатов наблюдения, рассчитывают среднее и предельное значение этой ошибки. Эти два параметра связаны между собой:
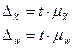 ;
;
где 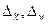 - предельные ошибки выборки для количественного и альтернативного атрибутивного признаков соответственно;
- предельные ошибки выборки для количественного и альтернативного атрибутивного признаков соответственно;
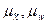 - средние ошибки выборки соответственно;
- средние ошибки выборки соответственно;
t – коэффициент доверия. Он зависит от вероятности, с которой гарантируется предельная ошибка выборки (доверительной вероятности).
Предельная ошибка выборки определяет предельные значения генеральной средней (доли), образующие доверительный интервал(слайд 2):
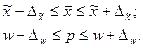
Предельная ошибка выборки характеризует точность результатов наблюдения, а доверительная вероятность – их достоверность. Для выборок большого объёма (не менее 30 единиц) коэффициент доверия зависит от доверительной вероятности (Р) следующим образом:
| P | 0,683 | 0,95 | 0,954 | 0,99 | 0,997 |
| t | 1,96 | 2,58 |
Порядок расчёта средней ошибки выборки зависит от способа выборочного наблюдения и метода отбора. При собственно-случайном наблюдении среднюю ошибку выборки определяют по формулам:
при повторном отборе
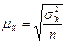 ;
;
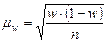 ;
;
при бесповторном отборе
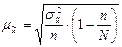 ;
;
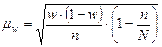 ,
,
где 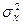 - выборочная дисперсия;
- выборочная дисперсия;
n – объём выборочной совокупности;
N – объём генеральной совокупности.
Средняя ошибка бесповторного наблюдения всегда меньше средней ошибки повторного наблюдения, так как всегда выполняется условие 0 < n/N < 1.
При большом объёме выборочной совокупности механическое наблюдение близко к бесповторному собственно-случайному отбору. В этом случае применяют формулы расчёта средней ошибки бесповторной собственно-случайной выборки.
При типическом наблюдение средняя ошибка выборки составляет:
при повторном отборе
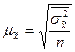 ;
;
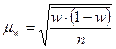 ;
;
при бесповторном отборе
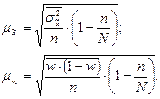
где 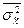 - средняя из внутригрупповых выборочных дисперсий;
- средняя из внутригрупповых выборочных дисперсий;
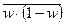 - средняя из внутригрупповых выборочных дисперсий доли.
- средняя из внутригрупповых выборочных дисперсий доли.
Условием применения этих формул является отбор единиц в типические группы пропорционально их числу в генеральных группах, когда:
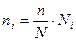 ,
,
где ni, Ni – число единиц в i-ой выборочной и генеральной группах соответственно.
При серийном наблюдении для расчета средней ошибки выборки используют следующие формулы:
при повторном отборе
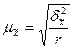 ;
;
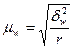 ;
;
при бесповторном отборе
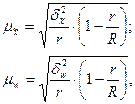
где 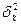 - межсерийная выборочная дисперсия;
- межсерийная выборочная дисперсия;
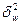 - межсерийная выборочная дисперсия доли;
- межсерийная выборочная дисперсия доли;
r - число отобранных серий;
R - число серий в генеральной совокупности.
Порядок расчёта всех видов выборочных дисперсий и взаимосвязь между ними аналогичны рассмотренны в разделе «Статистические показатели». При этом межсерийные дисперсии рассчитывают по формулам для расчета межгрупповых дисперсий. Отличие состоит в том, что все эти дисперсии рассчитывают не по генеральной совокупности, а по выборочной.
Определение необходимого объёма выборки
Перед проведением выборочного наблюдения необходимо определить объём будущей выборочной совокупности. Выбор объёма осуществляют, задаваясь точностью результатов наблюдения (предельной ошибкой выборки) и их достоверностью (доверительной вероятностью или коэффициентом доверия).
В таблице представлены формулы расчёта необходимого объёма выборки при различных способах наблюдения.
| Способ выборочного наблюдения | Повторный отбор | Бесповторный отбор |
| Собственно-случайный а) для среднего значения б) для доли Механический Типический а) для среднего значения б) для доли Серийный а) для среднего значения б) для доли | 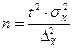
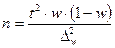 –
–
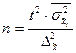
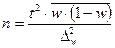
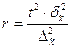
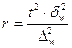
| 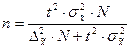
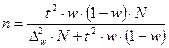 то же
то же
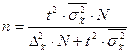
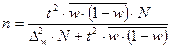
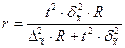
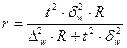
|
Применение этих формул требует знания выборочных дисперсий - общей, внутригрупповых или межсерийной. Их значения можно взять из результатов аналогичного наблюдения, проведённого ранее. Если такой возможности нет, то необходимо провести предварительное выборочное наблюдение небольшого объёма и по его результатам рассчитать выборочные дисперсии.
| <== предыдущая страница | | | следующая страница ==> |
| Обобщение и систематизация статистических данных | | | Статистические индексы |
Дата добавления: 2014-07-11; просмотров: 416; Нарушение авторских прав

Мы поможем в написании ваших работ!