
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Статистические индексы
Ошибка выборки или ошибка репрезентативности представляет собой разность соответствующих выборочных и генеральных характеристик:
Для средней количественного признака рассчитывается по следующей формуле:
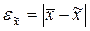 ;
;
где 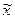 - выборочная средняя,
- выборочная средняя, 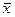 - генеральная средняя
- генеральная средняя
Для доли (альтернативного признака) рассчитывается по следующей формуле:
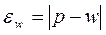
где w – выборочная доля, p - генеральная доля для альтернативного атрибутивного признака.
Ошибка выборки является случайной величиной, так как заранее неизвестно, какие единицы попадут в выборочную совокупность. Поэтому, оценивая точность результатов наблюдения, рассчитывают среднее и предельное значение этой ошибки. Эти два параметра связаны между собой:
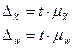 ;
;
где 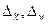 - предельные ошибки выборки для количественного и альтернативного атрибутивного признаков соответственно;
- предельные ошибки выборки для количественного и альтернативного атрибутивного признаков соответственно;
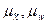 - средние ошибки выборки соответственно;
- средние ошибки выборки соответственно;
t – коэффициент доверия. Он зависит от вероятности, с которой гарантируется предельная ошибка выборки (доверительной вероятности).
Предельная ошибка выборки определяет предельные значения генеральной средней (доли), образующие доверительный интервал(слайд 2):
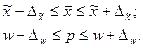
Предельная ошибка выборки характеризует точность результатов наблюдения, а доверительная вероятность – их достоверность. Для выборок большого объёма (не менее 30 единиц) коэффициент доверия зависит от доверительной вероятности (Р) следующим образом:
| P | 0,683 | 0,95 | 0,954 | 0,99 | 0,997 |
| t | 1,96 | 2,58 |
Порядок расчёта средней ошибки выборки зависит от способа выборочного наблюдения и метода отбора. При собственно-случайном наблюдении среднюю ошибку выборки определяют по формулам:
при повторном отборе
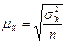 ;
;
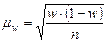 ;
;
при бесповторном отборе
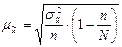 ;
;
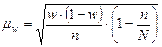 ,
,
где 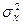 - выборочная дисперсия;
- выборочная дисперсия;
n – объём выборочной совокупности;
N – объём генеральной совокупности.
Средняя ошибка бесповторного наблюдения всегда меньше средней ошибки повторного наблюдения, так как всегда выполняется условие 0 < n/N < 1.
При большом объёме выборочной совокупности механическое наблюдение близко к бесповторному собственно-случайному отбору. В этом случае применяют формулы расчёта средней ошибки бесповторной собственно-случайной выборки.
При типическом наблюдение средняя ошибка выборки составляет:
при повторном отборе
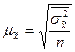 ;
;
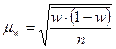 ;
;
при бесповторном отборе
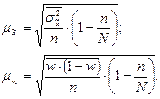
где 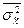 - средняя из внутригрупповых выборочных дисперсий;
- средняя из внутригрупповых выборочных дисперсий;
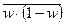 - средняя из внутригрупповых выборочных дисперсий доли.
- средняя из внутригрупповых выборочных дисперсий доли.
Условием применения этих формул является отбор единиц в типические группы пропорционально их числу в генеральных группах, когда:
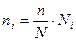 ,
,
где ni, Ni – число единиц в i-ой выборочной и генеральной группах соответственно.
При серийном наблюдении для расчета средней ошибки выборки используют следующие формулы:
при повторном отборе
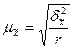 ;
;
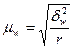 ;
;
при бесповторном отборе
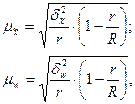
где 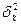 - межсерийная выборочная дисперсия;
- межсерийная выборочная дисперсия;
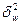 - межсерийная выборочная дисперсия доли;
- межсерийная выборочная дисперсия доли;
r - число отобранных серий;
R - число серий в генеральной совокупности.
Порядок расчёта всех видов выборочных дисперсий и взаимосвязь между ними аналогичны рассмотренны в разделе «Статистические показатели». При этом межсерийные дисперсии рассчитывают по формулам для расчета межгрупповых дисперсий. Отличие состоит в том, что все эти дисперсии рассчитывают не по генеральной совокупности, а по выборочной.
Определение необходимого объёма выборки
Перед проведением выборочного наблюдения необходимо определить объём будущей выборочной совокупности. Выбор объёма осуществляют, задаваясь точностью результатов наблюдения (предельной ошибкой выборки) и их достоверностью (доверительной вероятностью или коэффициентом доверия).
В таблице представлены формулы расчёта необходимого объёма выборки при различных способах наблюдения.
| Способ выборочного наблюдения | Повторный отбор | Бесповторный отбор |
| Собственно-случайный а) для среднего значения б) для доли Механический Типический а) для среднего значения б) для доли Серийный а) для среднего значения б) для доли | 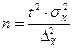
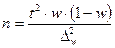 –
–
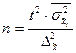
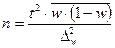
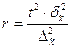
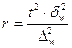
| 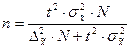
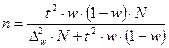 то же
то же
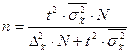
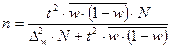
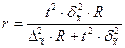
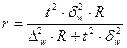
|
Применение этих формул требует знания выборочных дисперсий - общей, внутригрупповых или межсерийной. Их значения можно взять из результатов аналогичного наблюдения, проведённого ранее. Если такой возможности нет, то необходимо провести предварительное выборочное наблюдение небольшого объёма и по его результатам рассчитать выборочные дисперсии.
Статистические индексы
Индивидуальные и сводные экономические индексы
Экономический индекс – это относительная величина, показывающая, во сколько раз уровень социально-экономического явления в данных условиях отличается от его же уровня в других условиях. При этом различие условий может проявляться во времени, в пространстве или в сравнении с эталоном.
По степени охвата изучаемого явления различают индивидуальные и сводные экономические индексы.
Индивидуальные индексы характеризуют изменение отдельных элементов явления. Например, индивидуальным является индекс цен на молоко как элемент товаров молочной группы.
Индивидуальные индексы принято обозначать символом i.
Рассмотрим порядок расчета индивидуальных индексов на примере реализации конкретного товара.
Изменение цены товара характеризуется индивидуальным индексом цен:
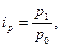
где р1, р0 – цена товара в текущем и базисном периоде соответственно.
Для оценки изменения объема реализации товара в натуральном выражении рассчитывают индивидуальный индекс физического объема:
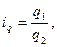
где q1, q2 – количество товара, проданного в отчётном и базисном периоде соответственно.
Произведение этих двух индексов дает индивидуальны индекс стоимости:
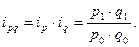
Этот индекс характеризует изменение товарооборота, то есть стоимости всего реализованного товара.
Аналогично рассчитывают индивидуальные индексы себестоимости (iz), издержек (izq), затрат рабочего времени на единицу продукции (it) и общих затрат рабочего времени (itq).
Таким образом, любой индивидуальный индекс показывает, во сколько раз изменилось значение индексируемого показателя для отдельного элемента явления (в нашем случае – для отдельного товара) при изменении условий его расчета (в нашем случае – при смене базисного периода на текущий).
Сводные экономические индексы
Сводные индексы характеризуют изменение какого-либо показателя, рассчитанного для группы элементов явления (например, изменение цен на товары молочной группы). Сводные индексы принято обозначать символом I.
Самый простой вариант расчета сводных индексов – расчет в агрегатной форме (agregat означает суммарный). Например, сводный индекс стоимости товаров определяют следующим образом:
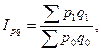
где p - цена на отдельные товары; q - их количество.
Этот индекс показывает, во сколько раз изменилась общая стоимость проданных товаров в текущем периоде относительно базисного.
Аналогично рассчитывают сводные индексы издержек (Izq) и общих затрат рабочего времени (Itq).
При расчете сводного индекса цен учитывают вес каждого товара в общем объеме реализации. Вес индекса -это показатель позволяющий соизмерить индексируемую величину.
Если веса берут из базисного периода, то имеет место сводный индекс цен Ласпейреса:
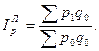
Разница между числителем и знаменателем показывает экономию или ущерб потребителей из-за изменения цен на товары:
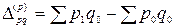 ;
;
Если веса берут из текущего периода, то говорят о сводном индексе цен Пааше:
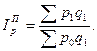
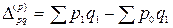 .
.
Оба индекса показывают, во сколько раз изменилась общая стоимость проданных товаров из-за изменения цен на них или, что то же самое, во сколько раз в среднем изменились цены на товары.
Аналогично рассчитывают сводные индексы себестоимости (Iz) и затрат рабочего времени на единицу продукции (It).
При расчете сводного индекса физического объема количество товара взвешивают по его цене (себестоимости, затратам рабочего времени). Например, сводный индекс физического объема, когда речь идет о реализации товаров, рассчитывают следующим образом:
по методу Ласпейреса
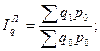
по методу Пааше
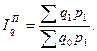
И в том, и в другом случае индекс показывает, во сколько раз изменилась общая стоимость реализованных товаров из-за изменения количества каждого из них или во сколько раз в среднем изменился физический объем реализации.
Для вычисления сводных индексов в агрегатной форме необходимы данные за оба сравниваемых периода. Если данные имеются только за один из периодов, но при этом известны индивидуальные индексы, то для расчета сводных индексов используют формулы средней – арифметической или гармонической.
Если, например, известны данные о стоимости товаров в базисном периоде и значения индивидуальных индексов стоимости, то сводный индекс стоимости рассчитывают по формуле средней арифметической:
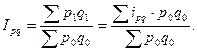
В этой формуле осредняют индивидуальные индексы стоимости, взвешивая их по стоимости товара в базисном периоде.
При наличии данных за текущий период используют формулу среднюю гармоническую:
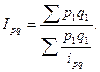
Аналогично рассчитывают сводные индексы издержек (Izq) и общих затрат рабочего времени (Itq).
На выбор формулы средней также влияет метод расчета сводного индекса – Ласпейреса или Пааше.
Например:
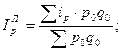
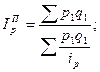
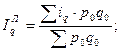
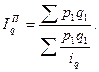
Аналогично рассчитывают сводные индексы себестоимости, затрат рабочего времени на единицу продукции и соответствующие им сводные индексы физического объема.
Между сводными индексами цен, физического объема и стоимости существует взаимосвязь:
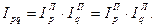
Аналогичные равенства выполняются для других сводных индексов.
В международной практике формула Лайспереса используется для расчета сводного индекса потребительских цен (ИПЦ) как отношения стоимости фиксированного набора товаров и услуг в текущем периоде к его стоимости в предыдущем (базисном) периоде. При этом методология исчисления ИПЦ предполагает расчет индекса для отдельных регионов, товарных групп и услуг.
С помощью ИПЦ номинальные доходы и заработную плату пересчитывают в реальные, учитывая таким образом наличие инфляции:
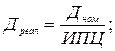
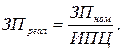
Индексы имеют экономический смысл. Разница между числителем и знаменателем в их формулах показывает экономию или ущерб потребителей из-за изменения цен на товары:
по Ласпейресу
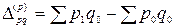 ;
;
по Пааше 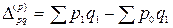 .
.
Системы экономических индексов
При изучении динамики уровней явления за три и более периодов времени формируют систему индексов. Например, при изучении динамики цен отдельного товара относительно базисного периода формируют систему индивидуальных базисных индексов цен:
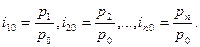
Если вместо постоянной базы сравнения используют предшествующие периоды, то имеет место система цепных индексов:
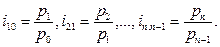
При изучении динамики многотоварных явлений используют системы сводных индексов. Например, система сводных индексов стоимости:
базисная
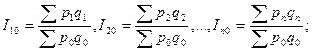
цепная
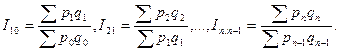
При взвешивании индексируемого показателя используют постоянные или переменные веса. Например, система сводных индексов физического объема с постоянными весами:
базисная
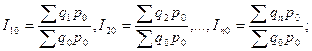
цепная
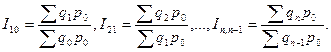
Если веса при переходе от одного индекса к другому меняются, то имеет место система сводных индексов с переменными весами. Например, система сводных индексов цен:
базисная
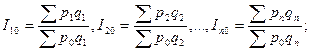
цепная
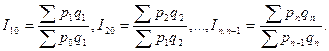
Базисные сводные индексы цен с переменными весами называют индексами-дефляторами. Их используют для пересчета номинальных значений стоимостных показателей в реальные (базисные). При этом номинальные значения делят на соответствующие им индексы-дефляторы.
Индивидуальные базисные и цепные индексы вязаны между собой:
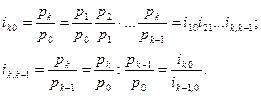
Аналогично связаны между собой базисные и цепные сводные индексы, рассчитываемые без весов или с постоянными весами:
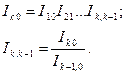
Для сводных индексов с переменными весами эти равенства не выполняются.
Индексы территориального сопоставления и средних статистических показателей.
При сравнении уровней явления в пространстве (по странам, регионам, областям) рассчитывают индексы территориального сопоставления – индивидуальные и сводные. Например, для сравнения цены, физического объема и стоимости реализации отдельного товара в регионе А по сравнению с регионом Б рассчитывают индивидуальные территориальные индексы цен, физического объема и стоимости:
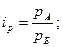
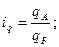
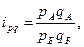
где 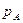 ,
, 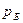 - цена товара в регионе А и регионе Б;
- цена товара в регионе А и регионе Б;
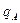 ,
, 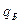 - физический объем его реализации в регионе А и регионе Б.
- физический объем его реализации в регионе А и регионе Б.
Если речь идет о группе неоднородных товаров, то рассчитывают сводные территориальные индексы. Например, сводный территориальный индекс стоимости:
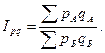
Расчет сводного территориального индекса цен осуществляют одним из двух способов – используя стандартные веса или сопоставляя каждый регион со средним уровнем цен.
Стандартный вес – это вес, соответствующий условной территории, полученной при объединении сравниваемых территорий. В нашем случае объединение регионов А и Б означает сложение значений физического объема в этих регионах по каждому виду товара. Следовательно, формула сводного индекса цен имеет вид:
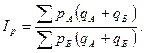
Такому индексу цен соответствует сводный индекс физического объема:
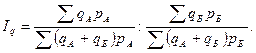
При использовании второго способа индекс цен рассчитывают по формуле:
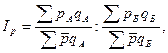
где 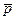 - среднее значение цены отдельного товара для регионов А и Б.
- среднее значение цены отдельного товара для регионов А и Б.
В паре с таким индексом цен рассчитывают сводный индекс физического объема:
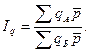
И в том, и в другом случае справедливо равенство:
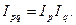
Аналогично рассчитывают индексы при территориальном сопоставлении себестоимости, издержек и затрат рабочего времени – на единицу продукции и общих.
Индексы средних статистических показателей
Рассмотрим порядок анализа динамики средних показателей на примере динамики средней цены одного товара, реализуемого разными торговыми предприятиями.
Средняя цена товара рассчитывается по формуле:
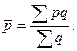
Из формулы следует, что динамика средней цены определяется двумя факторами – динамикой вариантов цены и динамикой структуры физического объема по этим вариантам. Для оценки влияния этих факторов рассчитывают:
индекс переменного состава
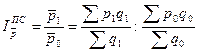 ;
;
индекс фиксированного состава
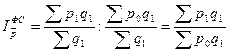 ;
;
индекс структурных сдвигов
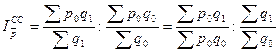 .
.
Индекс переменного состава показывает, во сколько раз изменилась средняя цена товара из-за одновременного изменения вариантов цены и структуры физического объема по этим вариантам. Индекс фиксированного состава показывает это только в части, касающейся первого фактора, а индекс структурных сдвигов – только в части второго.
Все три индекса связаны между собой:
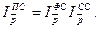
Аналогично индексируют другие средние статистические показатели.
| <== предыдущая страница | | | следующая страница ==> |
| Оценка точности и достоверности результатов выборочного наблюдения | | | Типология фигур человека |
Дата добавления: 2014-07-11; просмотров: 529; Нарушение авторских прав

Мы поможем в написании ваших работ!