ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СТАТИСТИЧЕСКИХ РАСПРЕДЕЛЕНИЙ

Для большей наглядности статистический ряд распределения случайной величины представляется графически в виде гистограмм, полигона, огивы.

Гистограмма - один из видов представления статистического распределения случайной величины. Гистограммы (столбчатые диаграммы) используются для наглядного представления и изучения распределений частот значений случайных величин. Такое частотное распределение показывает, какие именно конкретные значения или диапазоны значений исследуемой величины встречаются наиболее часто, насколько различаются эти значения, расположено ли большинство наблюдений около среднего значения, является распределение симметричным или асимметричным, многомодальным (т.е. имеет две или более вершины) или одномодальным и т.д. Гистограммы также используются для сравнения наблюдаемых и теоретических или ожидаемых распределений.

Наглядное представление распределения имеет важное практическое значение. Хотя конкретные (числовые) значения описательных статистик легко увидеть в таблице, в то же время общую структуру и глобальные характеристики распределения проще изучать с помощью графика. Более того, график дает качественную информацию о распределении, которую невозможно отразить с помощью какого-либо одного параметра. Например, по асимметрии распределения значений высоты нижней границы облаков в зимний сезон года можно сделать вывод о том, что в это время значительно чаще наблюдается низкая облачность. Хотя эта информация содержится в значении коэффициента асимметрии, но она легче воспринимается и запоминается, будучи графически представленной на гистограмме. Кроме того, на гистограмме можно наблюдать некоторые «впадины и выпуклости», которые могут свидетельствовать о преобладании тех или иных значений высоты облачности, о более высокой повторяемости некоторых атмосферных процессов и т.д.

По форме распределения можно судить и о природе исследуемой переменной (например, бимодальное распределение позволяет предположить, что выборка не является однородной и содержит наблюдения, принадлежащие двум различным множествам, которые в свою очередь нормально распределены). Не случайно, по мнению некоторых исследователей, работа с новым набором данных начинается с построения гистограмм всех переменных.

Ниже будут рассмотрены два вида гистограмм - гистограммы дифференциального и интегрального распределения. Названия их обусловлены соответствующими зависимостями между плотностью и функцией распределения.

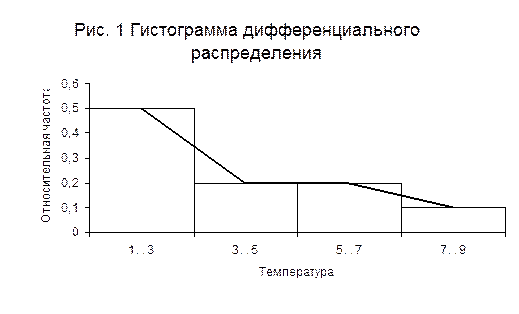
Гистограмма дифференциального распределения (частот распределения) строится следующим образом. На оси абсцисс выбранной прямоугольной системы координат отмечаются точки х₁, х₂, ..., х_k+1, соответствующие границам градаций представляемого статистического ряда распределения. Затем на каждом полученных отрезков как на основании строится прямоугольник с высотой, равной численности соответствующей градации (абсолютной частоте, повторяемости и т.д.).

Гистограмма интегрального распределения (накопленных частот) строится аналогично гистограмме дифференциального распределения. На оси абсцисс выбранной прямоугольной системы координат отмечаются границы градаций представляемого статистического ряда. Затем на каждом из полученных отрезков как на основании строится прямоугольник, высота которого равна сумме частот всех градаций, лежащих левее правой границы градации.

Примеры графического представления распределения температуры воздуха приведены на рис. 1-2. На рис. 1 также построен полигон распределения (см. ниже по тексту).

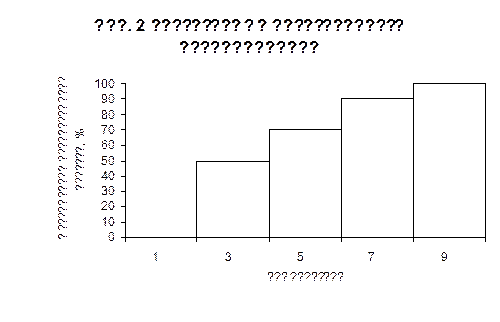
После построения гистограммы интегрального распределения верхние стороны полученных прямоугольников можно выделить жирными линиями. В результате такой операции получится разрывная ступенчатая кривая, которая представляет собой график статистической функции распределения. Точки разрыва на графике накопленных частот соответствуют границам градаций. Скачок в каждой из этих точек численно равен частоте предшествующей градации.

Кроме гистограмм для графического отображения статистических распределений используются ломаные линии, называемые полигоном и огивой.

Полигон представляет собой график, на котором распределение частот по градациям изображается точками, соединенными последовательно отрезками прямых. Он строится следующим образом. На оси абсцисс выбранной прямоугольной системы координат отмечаются середины градаций представляемого статистического ряда. Затем на график наносятся точки, абсциссами которых являются середины градаций, а ординатами - соответствующие им частоты, и соединяются последовательно отрезками прямых. (См. рис. 1).

Огиватакжеявляется способом графического представления накопленных численностей. Для ее построения на поле графика наносятся точки, соответствующие границам градаций, а ординатами - соответствующие им накопленные частоты. Затем эти точки соединяются отрезками прямых. Понятно, что огива является эмпирическим аналогом функции распределения.

ЗАКЛЮЧЕНИЕ

В данной лекции были изучены основные численности статистических распределений. На очередном практическом занятии необходимо будет научиться определять их практически, используя для этой цели сформированную архивную выборку.

Следующей лекция будет посвящена вопросам, связанным с принятием статистических решений и необходимыми для этого показателями и критериями.

Дата добавления: 2014-07-19; просмотров: 537; Нарушение авторских прав

Мы поможем в написании ваших работ!