Лекция №13 Трехмерные дефекты малого объема - дисперсные выделения в матрице кристалла

Для большей наглядности статистический ряд распределения случайной величины представляется графически в виде гистограмм, полигона, огивы.

Гистограмма - один из видов представления статистического распределения случайной величины. Гистограммы (столбчатые диаграммы) используются для наглядного представления и изучения распределений частот значений случайных величин. Такое частотное распределение показывает, какие именно конкретные значения или диапазоны значений исследуемой величины встречаются наиболее часто, насколько различаются эти значения, расположено ли большинство наблюдений около среднего значения, является распределение симметричным или асимметричным, многомодальным (т.е. имеет две или более вершины) или одномодальным и т.д. Гистограммы также используются для сравнения наблюдаемых и теоретических или ожидаемых распределений.

Наглядное представление распределения имеет важное практическое значение. Хотя конкретные (числовые) значения описательных статистик легко увидеть в таблице, в то же время общую структуру и глобальные характеристики распределения проще изучать с помощью графика. Более того, график дает качественную информацию о распределении, которую невозможно отразить с помощью какого-либо одного параметра. Например, по асимметрии распределения значений высоты нижней границы облаков в зимний сезон года можно сделать вывод о том, что в это время значительно чаще наблюдается низкая облачность. Хотя эта информация содержится в значении коэффициента асимметрии, но она легче воспринимается и запоминается, будучи графически представленной на гистограмме. Кроме того, на гистограмме можно наблюдать некоторые «впадины и выпуклости», которые могут свидетельствовать о преобладании тех или иных значений высоты облачности, о более высокой повторяемости некоторых атмосферных процессов и т.д.

По форме распределения можно судить и о природе исследуемой переменной (например, бимодальное распределение позволяет предположить, что выборка не является однородной и содержит наблюдения, принадлежащие двум различным множествам, которые в свою очередь нормально распределены). Не случайно, по мнению некоторых исследователей, работа с новым набором данных начинается с построения гистограмм всех переменных.

Ниже будут рассмотрены два вида гистограмм - гистограммы дифференциального и интегрального распределения. Названия их обусловлены соответствующими зависимостями между плотностью и функцией распределения.

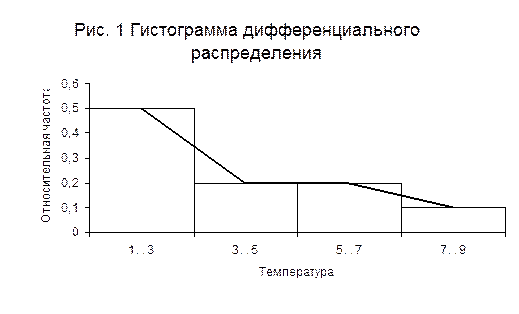
Гистограмма дифференциального распределения (частот распределения) строится следующим образом. На оси абсцисс выбранной прямоугольной системы координат отмечаются точки х₁, х₂, ..., х_k+1, соответствующие границам градаций представляемого статистического ряда распределения. Затем на каждом полученных отрезков как на основании строится прямоугольник с высотой, равной численности соответствующей градации (абсолютной частоте, повторяемости и т.д.).

Гистограмма интегрального распределения (накопленных частот) строится аналогично гистограмме дифференциального распределения. На оси абсцисс выбранной прямоугольной системы координат отмечаются границы градаций представляемого статистического ряда. Затем на каждом из полученных отрезков как на основании строится прямоугольник, высота которого равна сумме частот всех градаций, лежащих левее правой границы градации.

Примеры графического представления распределения температуры воздуха приведены на рис. 1-2. На рис. 1 также построен полигон распределения (см. ниже по тексту).

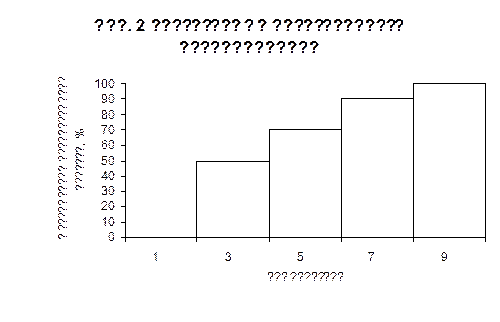
После построения гистограммы интегрального распределения верхние стороны полученных прямоугольников можно выделить жирными линиями. В результате такой операции получится разрывная ступенчатая кривая, которая представляет собой график статистической функции распределения. Точки разрыва на графике накопленных частот соответствуют границам градаций. Скачок в каждой из этих точек численно равен частоте предшествующей градации.

Кроме гистограмм для графического отображения статистических распределений используются ломаные линии, называемые полигоном и огивой.

Полигон представляет собой график, на котором распределение частот по градациям изображается точками, соединенными последовательно отрезками прямых. Он строится следующим образом. На оси абсцисс выбранной прямоугольной системы координат отмечаются середины градаций представляемого статистического ряда. Затем на график наносятся точки, абсциссами которых являются середины градаций, а ординатами - соответствующие им частоты, и соединяются последовательно отрезками прямых. (См. рис. 1).

Огиватакжеявляется способом графического представления накопленных численностей. Для ее построения на поле графика наносятся точки, соответствующие границам градаций, а ординатами - соответствующие им накопленные частоты. Затем эти точки соединяются отрезками прямых. Понятно, что огива является эмпирическим аналогом функции распределения.

ЗАКЛЮЧЕНИЕ

В данной лекции были изучены основные численности статистических распределений. На очередном практическом занятии необходимо будет научиться определять их практически, используя для этой цели сформированную архивную выборку.

Следующей лекция будет посвящена вопросам, связанным с принятием статистических решений и необходимыми для этого показателями и критериями.

Лекция №13 Трехмерные дефекты малого объема - дисперсные выделения в матрице кристалла.

Дисперсные когерентные включения вызывают появление контраста прежде всего вследствие деформации окружающей матрицы. Поле смещений u зависит от анизотропии размеров и упругих свойств включений и матрицы. Критерий наблюдаемости позволяет определить направление u (линия отсутствия контраста всегда перпендикулярна направлению Н). Это позволяет различать пластинчатые, сферические и стержнеобразные включения. В простейшем случае сферического выделения в упруго изотропной матрице поле смещений задается формулой:

,

где А= - мощность дефекта (здесь n число атомов (молекул) во включении,

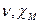- коэффициент Пуассона и сжимаемость матрицы,

- сжимаемость включения,

R^M, R^B-эффективный радиус атомов ( молекул в решетке матрицы и включения).

Поле смещений частицы обладает сферической симметрией, поэтому линия от сутствия контраста, где , проходит перпендикулярно направлению вектора Н, формирующего изображение. Изображение возникает благодаря тому, что плоскости в колонках искривляются, некоторые участки колонки приближаются брэгговскому положению (рис23). При этом амплитуда дифрагированного пучка возрастает. Изображение включения обусловленное искажением матрицы, имеет вид двух полуколец, разделенных линией отсутствия контраста. При этом вид изображения сохраняется при переходе от одного к другому отражению, формирующему изображение. Так как искривление колонки выше и ниже частицы имеет разные знаки, контраст, особенно для частиц малого размера, слабый, обычно лучше всего такие частицы видны при s~0, когда контраст возникает в результате интерференционного поглощения блоховской волны. При этом в темнопольном изображении частиц, находящихся вблизи нижней поверхности фольги, наблюдается характерный черно- белый контраст. По характеру расположения темных и светлых областей удается различить включения типа «внедрения» и «вычитания».В первом случае смещения направ- лены от частицы вдоль радиуса (А>0), во втором- наоборот. Для включений типа «внедрения» изображение на темнопольном позитивном отпечатке имеет чередование контраста от светлого к темному в положительном направлении вектора Н, так как это показано на рисунке 24. Мощность дефекта А можно, в принципе, найти из анализа профиля изображения вдоль направления вектора Н по методике, предложенной Эшби М. и Брауном Л.

На рисунке 25 показана зависимость ширины изображения, нормированной на экстинкционую длину (L _Э) от . Этот график и может быть использован для нахождения мощности дефекта А. Чтобы частица была видна в микроскоп, максимальная разница интенсивностей в области изображения частицы и фона должна быть больше определенной величины (например 10%). Условие видимости по Эшби М. и Брауну Л. имеет вид:

,

где R₀-радиус частицы.

В принципе анализ дифракционного контраста для малых дислокационных петель и пластинчатых выделений аналогичен, но при расчете амплитуд колонок подставляется поле смещений для этих дефектов. Если плоскость залегания круглой петли параллельна плоскости фольги, то вид изображения аналогичен изображению сферической частицыю Если петля расположена в наклонной плоскости, то проекция векторов смещения на плоскость фольги эллипс и расстояние между полукольцами изображения и симметрия их взаимного расположения будут зависеть от направления вектора дифракции (при прочих равных условиях формирования изображения).

Выделения можно обнаружить не только за счет контраста, обусловленного деформацией матрицы вокруг выделения. В частности, если структурные амплитуды решеток матрицы и когерентного выделения заметно различаются, так же может возникнуть контраст. Эшби М.и Браун Л. показали, что если толщина выделений 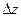<<L_э для формирующего контраст отражжения, то при s относительное изменение интенсивности будет равно:

.

Очевидно наилучшие условия контраста будут если Очевидно, что в случае контраста из-за различия структурных амплитуд светлопольное и темнопольное изображения должны давать взаимно дополняющий контраст, если можно пренебречь поглощением. При сильном поглощении в толстых фольгах этот контраст будет очень слабым. Кроме того, при различной ориентации решеток матрицы и выделения, приводящей к заметному различию условий дифракции (при частично или полностью некогерентном выделении) в этих решетках может появиться так называемый ориентационный контраст. Этот тип контраста чаще всего встречается при достаточно крупных выделениях. В этом случае темнопольные изображения в рефлексах от выделений весьма полезный способ получить изображения выделений и установить их форму и размеры. Ориентационный контраст может приводить к появлению на краях изображений частиц полос равной толщины, аналогичных наклонным высокоугловым границам зерен.

Наконец, еще один тип контраста- контраст типа полос смещения, возникающий при резком изменении фазы падающей и дифрагированной волн на границе матрицы и выделения. В случае частично когерентного пластинчатого выделения вектор смещения перпендикулярный плоскости пластинки определяется формулой:

,

где 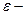относительная разница межплоскостных расстояний матрицы и выделения,

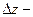толщина пластинки,

n- число дислокаций несоответствия с компонентой вектора Бюргерса 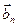, нормальной плоскости пластинки.

Если при s изменение фазы кратно 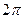, то контраста нет. Но если (где n=1,2…),то при наклонном залегании пластинки на изображении возникает периодическое изменение интенсивности, независимое от (похожее на контраст от дефекта упаковки). Фазовый угол влияет на амплитуду колебаний интенсивности по глубине. Периодичность же не зависит от вектора смещения и равна L_Э/2. При s , в частности, при L_Эs ампликолебаний интенсивности становится малой и при эти дополнительные колебания исчезают и периодичность становится равной эффективной экстинкционной длине .

В последние годы все большее распространение получают высоковольтные микроскопы с энергией электронов большей 350 кэВ о даже 1—1,5 МэВ. Такие микроскопы применяются прежде всего прежде всего из-за возможности увеличения толщины просвечиваемых фольг, что приближает условия наблюдения реальной структуры к структуре объемных объектов и увеличивает статистическую достоверность изучения особенностей структуры за счет увеличения просвечиваемого объема. При этом возрастает и толщина образца с заданным уровнем хроматической аберрации, обеспечивающим высокое разрешение микроскопа. Уменьшение рабочей длины волны с ростом ускоряющего напряжения обеспечивает и повышение теоретического разрешения и возможность прямого разрешения решетки за счет уменьшения углов дифракции (см.ниже).

Дата добавления: 2014-07-19; просмотров: 377; Нарушение авторских прав

Мы поможем в написании ваших работ!