Получение изображений с фазовым контрастом

В этом случае изображение формируется в результате интерференции нескольких дифрагированных пучков. Рассмотрим сначала простейший случай ,наблюдаемый даже в микроскопах с неочень высоким разрешением, когда реальные межплоскостные расстояния в решетке меньше разрешающей способности микроскопа. В образце, представляющем собой кристаллическую матрицу и включение в результате двойной дифракции в окрестности рефлексов электронограммы матрицы появляются рефлексы. расстояние до которых существенно меньше, чем расстояние между узлами матрицы (рис.25). Апертура позволяет достичь плоскости изображения, например, прямому и дважды дифрагированному пучку. В этом случае влиянием аберраций и дефокусировки, так как микроскоп работает не на пределе разрешающей способности, можно пренебречь. Тогда амплитуда А(r) в точке r определяется суммой амплитуд двух когерентных волн:

(8)

где А_0, А₁₂ - амплитуды прошедшей и дважды дифрагированной волн,

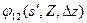, - фазы волн, покидающих образец, зависящие от условий отражения (s,s^’) и толщины фольги Z и включения ,

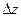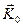-волновой вектор падающей волны.

В результате на изображении появятся линии равного значения амплитуды при . Итак для данных условий дифракции (s,Z), если А₁₂ соизмерима с А₀ возникает периодически меняющийся контраст (изменение интенсивности) с периодичностью в виде линий одинаковой интенсивности перпендикулярных 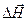. Эти линии называются муаровым узором. На схеме электронограммы (рис.26) показан пучок Р₁, отраженный от плоскостей матрицы с межплоскостным расстоянием d₁. После отражения от плоскостей включения с межплоскостным расстоянием d₂ дважды отраженный луч попадает в точку Q₁. Центр электронограммы и точки Р₁и Q₁лежат на одной прямой , если плоскости матрицы и включения параллельны. Отрезки ОР₁ и Р₁Q₁ пропорциональны 1/d₁ и 1/d₂ а OQ₁ cоответственно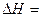 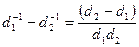. Очевидно, что в точку Q₁ попал бы пучок, отраженный от плоскостей с межплоскостным расстоянием . Если через апертуру проходят пучки О и Q₁, то в соответствии с формулой (8) получается увеличенное изображение периодической структуры с периодом 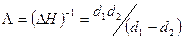. Полосы равной интенсивности муарового узора смещения перпендикулярны вектору Если последовательное отражение происходит от плоскостей с одинаковым межплоскостным расстоянием, но повернутых на малый угол вокруг оси электронного пучка, то практически перпендикулярен Н₁ и равен 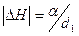. Соответственно период полос муарового узора вращения, перпендикулярных 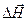равен . При сопряжении решеток с разными периодами ималым взаимным разворотом возникает смешанный муаровый узор с периодом 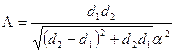. При разделении перекрывающихся решеток в фольге границей кручения может возникнуть муар вращения. Расстояние( D) между соседними винтовыми дислокациями в такой границ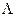е = , где 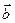-вектор Бюргерса, -угол скручивания. Если кристалл разделен на две части плоскостью скольжения, содержащей ряд краевых дислокаций одного знака, то среднее межплоскостное расстояние в той части кристалла , где лежат избыточные полуплоскости меньше. В результате может возникнуть картина муара смещения, полосы которой параллельны осям дислокаций , причем при 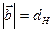расстояние между полосами муара равно расстоянию между дислокациями. Ряд смешанных дислокаций должен давать картину смешанного муара. Анализ полос муара часто является способом установления характера сопряжения матрицы и выделения. Чтобы представить влияние отдельных дислокаций на муаровый узор учтем, что он получается наложением решеток совершенного и несовершенного кристаллов и является увеличенным изображением периодической структуры несовершенного кристалла .Если, например, в нижний слой сендвича, дающего муаровый узор, ввести дислокацию, то полосы муара на одной стороне изображения сместятся по отношению к полосам на другой стороне на величину, равную проекции вектора Бюргерса на нормаль к отражающим плоскостям. Это приведет ктому, что ряд полос обрывается на дислокации. Если дислокация находится в решетке с меньшим периодом то дислокация в муаровом узоре (для муара смещения ) имеет тот же знак что и дислокация в решетке. Но если дислокация находится в решетке с большим периодом то в муаровом узоре дислокация имеет противоположный знак (рис 27). Число оборванных полос равно отношению проекции вектора Бюргерса на единичный вектор нормали к отражающим плоскостям , деленной на межплоскостное расстояние изображаемых плоскостей:

.

Для полных дислокаций N - целое число, для частичных может быть и дробным. Это означает, что полосы смещены не на целый период, а лишь на его часть. Изображение имеет одинаковый вид для краевой и винтовой дислокаций. Из изложенного следует, что по обрывающимся (смешанным) полосам муарового узора можно найти проекцию вектора Бюргерса. Если величина вектора Бюргерса не известна, как это бывает для кристаллов со сложными решетками, то, получив проекции на три некомпланарных вектора Н, можно найти его величину и направление.

Если в каждой из налагающихся решеток имеется по дислокации то число оборванных полос равно разности между значениями N для каждой дислокации, когда они имеют одинаковый знак, и сумме значений N если они имеют противоположные знаки. Определенный практический интерес имеет возможность наблюдения муара в эпитаксиальных структурах, особенно если удается осуществлять непосредственно в колонне микроскопа. Удается заметить уже незначительные взаимные повороты решеток при образовании зародышей - кристаллов растущей пленки. При этом можно проследить зависимость разориентации решеток от их рамеров, образование дислокаций при приспособлении решеток и в процессе роста сплошной пленки при сравтании зародышей.

Дата добавления: 2014-07-19; просмотров: 342; Нарушение авторских прав

Мы поможем в написании ваших работ!