ОСНОВНЫЕ ЧИСЛЕННОСТИ СТАТИСТИЧЕСКИХ РАСПРЕДЕЛЕНИЙ

Абсолютной частотой градации называется число случаев попадания наблюденных значений случайной величины (элементов выборки) в данную градацию. Она показывает, как часто могут появляться значения случайной величины из данной градации. Абсолютную частоту i-ой градации будем обозначать через m_i. Очевидно, что 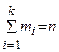, где n - объем архивной выборки.

Абсолютная частота обладает тем недостатком, что она не является показательной характеристикой для выборок разных объемов. Если требуется проводить сравнительный анализ статистических распределений для выборок разных объемов, то удобнее пользоваться понятием относительной частоты.

Относительной частотойградации называется отношение абсолютной частоты соответствующей градации к общему числу обрабатываемых наблюдений n. Обозначается относительная частота обычно через 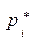и вычисляется по формуле:

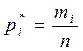(6)

Из определения следует, что 0 £ p_i^* £ 1, и сумма частот всех градаций равна единице, т.е.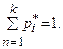

Относительная частота градации является оценкой вероятности попадания случайной величины в данную градацию. В метеорологии относительную частоту часто называют повторяемостью.

Абсолютная и относительная частоты являются основными численностями дифференциального распределения, и в случае, если все градации равны между собой, ограничиваются их вычислениями. Если же в статистическом распределении имеются градации разной ширины, то эти численности теряют свою наглядность и показательность. Тогда рассчитываются абсолютные и относительные плотности.

Абсолютной плотностью градации называется отношение абсолютной частоты данной градации к ее ширине Dx , т.е.

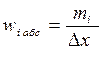. (7)

Относительной плотностью градации называется отношение относительной частоты данной градации к ее ширине, т.е.

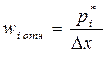. (8)

Относительная плотность градации является приближенной оценкой плотности распределения вероятностей в данном интервале для серединного значения i-ой градации, т.е. w_1отн » f (x₁).

Отсюда можно сделать вывод, что статистический ряд, численностями которого являются относительные плотности градаций, может служить подходящей параметрической оценкой (статистическим аналогом) плотности распределения исследуемой случайной величины. При этом, чем больше будет объем обрабатываемой выборки и чем меньше будут градации, тем точнее статистический ряд будет воспроизводить теоретическую плотность распределения исследуемой случайной величины.

Абсолютной накопленной частотой называется число случаев попадания наблюденных значений случайной величины X (элементов выборки) в интервал от - ¥ до правой границы i-ой градации х_i, т.е. это есть число случаев наблюдений значений величины X, меньших, чем х_i. Абсолютная накопленная частота обозначается через m(X<x_i) и вычисляется обычно с использованием дифференциального статистического ряда по формуле

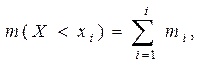(9)

где х_i - правая граница i-той градации;

m_j - абсолютная частота i-той градации;

m(X<x_i) - есть сумма частот от 1-ой до i-той градации.

Относительной накопленной частотой называется относительная частота наблюдений случайной величины Х в интервале от - ¥ до x_i. Она обозначается через 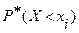и вычисляется обычно с использованием данных дифференциального статистического распределения по формуле:

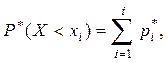(10)

где x_i - правая граница i-той градации;

р_j^* - относительная частота i-той градации.

Из приведенных определений следует, что статистический ряд, численностями которого являются накопленные частоты, может служить оценкой функции распределения. Такую оценку функции распределения F(x) принято называть статистической функцией распределения и обозначать через F^*(x). Иногда она называется выборочной функцией распределенияилиэмпирической функцией распределения и имеет вид:

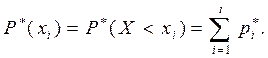(11)

Если для практических целей требуется знать абсолютную или относительную частоту появления значений X, больших некоторого заданного x_i, то используются формулы:

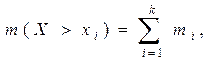(12)

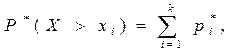(13)

где x_i - левая граница i-той градации.

Дата добавления: 2014-07-19; просмотров: 344; Нарушение авторских прав

Мы поможем в написании ваших работ!