Статистический ряд распределения и порядок его построения

Из обсуждения контраста, вызванного полями смещений дислокаций, видно, что в принципе вектор Бюргерса определяется путем нахождения двух рефлексов (темнопольные изображения), в которых дислокация не дает контраста , т.е. для которых (Hb)=0. Линия пересечения соответствующих атомных плоскостей параллельна вектору Бюргерса. Однако, это обычно хорошо выполняется только для винтовой дислокации, так как в общем случае благодаря компоненте смещений u₃ изображение дислокации может и не исчезать полностью при (Hb)=0. Поэтому для однозначного определения направления вектора Бюргерса необходима проверка выполнения и условия (Hb)=0 и условия (Hu₃)=0. Методика конкретного эксперимента может видоизменяться в зависимости от ориентации смещений u₂ и u₃ по отношению к плоскости фольги, так как возможные повороты фольги относительно электронного пучка ограничены возможностями гониометрического устройства микроскопов. Рассмотрим определение вектора Бюргерса полной дислокации в гранецентрированной кубической решетке.Примем, что плоскость фольги совпадает с плоскостью (111). Пусть дислокация, лежащая плоскости фольги, имеет один из векторов Бюргерса параллельных плоскости (111): (а/2)[ 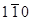], (а/2)[10 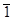] или (а/2)[0 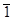1]. Тогда в одном из трех отражений 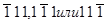, которые при заданной ориентировке фольги легко получаются наклоном фольги на угол около 20⁰, (Hb)=0 и изображение любого типа дислокаций (винтовые, краевые или смешанные) «гаснет» .Это определяется тем, что произведение (Hu₃) мало, так как вектор u₃ почти перпендикулярен вектору дифракции. Так если вектор 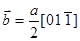, то в отражениях 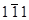и и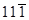зображения есть, а в отражении 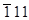его нет. Подобное же сопоставление можно сделать и для двух других векторов Бюргерса.

Рассмотрим теперь дислокации, имеющие один из векторов Бюргерса, не лежащих в плоскости (111): 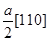, 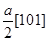или 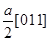. Пусть, например, имеется дислокация с вектором 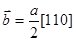. Если линия дислокации параллельна плоскости (111), составляющая поля смещений u₂ лежит в плоскости 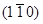. В этом случае в отражении 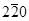, которое при данной ориентировке фольги так же легко получить, изображение дислокации отсутствует. Изображение этой дислокации, практически, не видно и в отражении .

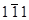При определении векторов Бюргерса частичных дислокаций в ГЦК решетке удобно исследовать фольгу, вырезанную по плоскости (110), используя отражения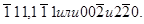

Векторы Бюргерса дислокаций Шокли можно найти из анализа контраста в этих четырех отражениях, учитывая, что при не слишком больших значениях s дислокации видны, если (Hb)= 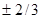и не видны если (Hb)= 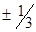. Для того чтобы отличить дислокации Шокли от дислокаций Франка, следует учесть еще, что последняя является краевой дислокацией и,следовательно имеет компоненту u₃, влияющую на контраст.

Анализ контраста на изображениях дислокаций позволяет определить знак вектора Бюргерса, то есть решить, находится ли дополнительная полуплоскость краевой дислокации выше или ниже плоскости скольжения. Эта задача тесно связана с задачей об определении природы дислокационных петель, возникающих в кристаллах при ассоциации точечных дефектов. На рис.17 схематически изображены две краевые дислокации противоположного знака и показан наклон атомных плоскостей, вызванный их полями смещений. Там же стрелкой показан поворот, при котором кристалл приближается к строго брегговскому положению. Очевидно, что изображения дислокаций будут расположены там, где плоскости решетки повернуты в направлении С. При повороте кристалла вокруг оси, перпендикулярной пучку электронов и вектору дифракции на такой угол, при котором абсолютная величина вектора s остается неизменной, а знак меняется на противоположный, изображения дислокаций переместятся в разные стороны так как это показано на рисунке стрелками А.

В деформированных кристаллах часто наблюдаются дислокации противоположного знака, лежащие в параллельных плоскостях скольжения. Различие знаков векторов Бюргерса дислокаций можно установить по смещению изображений при изменении знака s. На рисунке 18а показаны призматические дислокационные петли вакансионного и внедренного типа, наклоненные к направлению электронного пучка, а также направление вектора дифракции H. Отклонение от строго брегговских условий дифракции таковы, что s> 0. Стрелками показаны направления локальных поворотов решетки, приближающих участки кристалла к положению s=0, которым и соответствует положение изображения.

Если изменить знак s вращая кристалл, то , в соответствии с вышеизложенным, изображе- ние петли переместится так, как это показано на рисунке 18а.Таким образом, изменение размера изображения петли позволяет отличить петли вакансионного и внедренного типов. Легко убедиться, что то же изменение геометрии изображения будет, если оставить неизменным знак и величину s, изменив направление вектора дифракции Н. Следует отметить, что для однозначного определения типа петли необходимо знать плоскость наклона петли (рис. 18). Анализируя изменение формы петли при наклоне образца на большой угол вокруг нормали к отражающей системе плоскостей (при сохранении условия s=соnst ), можно это найти.

При исследовании петель Франка для оценки их размеров можно так вырезать фольгу, чтобы плоскость залегания петель или хотя бы части петель была параллельна плоскости фольги. В этом случае на контраст влияет только компонента поля смещений u₃ и изображение располагается симметрично относительно линии дислокаций.Важным аспектом исследования дислокационных петель является подсчет числа петель с учетом части петель, невидимых в данном отражении, при определении концентрации точечных дефектов, скоагулированных в петли. До сих пор при обсуждении контраста на дислокациях мы не учитывали, что наблюдение ведется в весьма тонких слоях и что поверхностные релаксационные эффекты могут приводить к смещениям, дающим контраст. Рассмотрим два характерных примера.

Пусть в очень тонкой фольге имеется краевая дислокация с осью, параллельной плоскости фольги. Такая дислокация создает поворот фольги 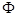(рис. 19):

,

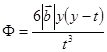где 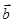- вектор Бюргерса,

t-толщина фольги,

y-глубина залегания дислокации под поверхностью.

Знак изгиба (при известном s), определяемый по изменению контраста, разделенных дислокацией участков, а количественно по смещению кикучи-линий, позволяет определить знак вектора Бюргерса. Особенно существенны релаксационные эффекты для дислокаций, ось которых нормальна к плоскости фольги. В частности, для винтовой дислокации с осью, нормальной к плоскости фольги, выполняется условие (Hb)=0 и в бесконечно толстом кристалле она была бы не видна. Но вблизи поверхности такая дислокация вызывает скручивание решетки вокруг своей оси. В результате плоскости ранее параллельные оси дислокации, слегка наклоняются, как это показано на рисунке 20. Вдоль линии, проходящей через центр дислокации параллельно Н, смещения параллельны отражающим плоскостям и контраста не дают. Характер контраста на изображении по обе стороны от этой линии при известных H и s позволяют отличить левовинтовую и правовинтовую дислокации. Краевые дислокации, нормальные плоскости фольги, из-за малых величин углов Брегга не должны давать контраста от сжатых и растянутых областей, так как при этом почти не меняется 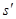в формуле (6). Но при 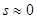расчеты, расчеты, выполненные на основе динамической теории показали, что так же возникает черно-белый контраст. Так в растянутой области кристалла (локальное значение 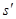>0) возникает и на светлопольном и на темнопольном изображении одинаковый абсорбционный контраст. В то же время в сжатой области ( 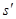<0) контраст на светлои темнопольном изображениях взаимно дополнительный.

Плоские дефекты. Простейшим плоским дефектом является дефект упаковки, поскольку по обе стороны дефекта упаковки решетка имеет одинаковые параметры и ориентацию, но сдвинута на некоторый постоянный вектор u. Рассчитаем амплитуду, рассеянную колонкой , показанной на рисунке 21. Амплитуда, рассеянная верхней частью колонки равна:

А₁~ .

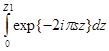Для продолжения этой колонки, лежащей ниже дефекта упаковки ,координаты ячеек определяются с учетом сдвига на вектор смещения u ,который не зависит от z, получим:

А_{2 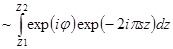,} где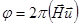

Суммарная амплитуда равна А= А₁+А₂.Если вектор u равен вектору трансляции 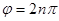(n=1,2,3 ), дефект невидим для всех отражений Н. Если же вектор u не равен вектору трансляции, то могут быть такие отражения, для которых n – нецелое число. Поэтому идентификация отражений, в которых дефект невидим, позволяет определить вектор смещения u. Рассмотрим пример. В широко распространенной гранецентрированной кубической структуре дефекты упаковки лежат в плоскостях {111} и могут быть образованы или сдвигом с вектором сдвига (а/6)<112> или сжатием решетки на вектор 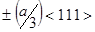. Хотя частичные дислокации в этих случаях не одинаковы, однако, их векторы Бюргерса различаются на вектор трансляции (а/2)<110> и, с точки зрения контраста , вектор u, учитывая периодичность функции 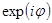, одинаков и можем положить его равным 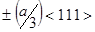. Это соответствует или внедрению, или удалению слоя атомов – соответственно дефект внедрения или вычитания.

Для отражения Н и дефекта с вектором сдвига u= 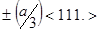имеем 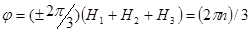, где n=0,1,2…В тех случаях, когда значение n не равно нулю и не кратно 3, дефект упаковки виден, так как влияет на величину амплитуды А. Для того чтобы представить характер контраста, обусловленного дефектом упаковки, построим амплитудно-фазовую диаграмму для волн, рассеянных колонкой, пересекаемой дефектом упаковки в точке z, расположенной на глубине Z/2. Пусть длина колонки величина вектора s таковы, что Zs>>1. Для совершенного участка кристалла амплитудно–фазовая диаграмма представляет собой окружность радиусом 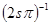. В колонке с дефектом в точке z происходит скачкообразное изменение фазы на 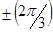. Для нижней части колонки кривизна амплитудно- фазовой диаграммы остается прежней. Соответствующая амплитудно-фазовая диаграмма показана на рисунке 21б. Вектор 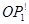отвечает амплитуде колонки совершенного кристалла, а вектор ОР₁ амплитуде колонки пересекаемой дефектом в точке z. При изменении положения колонки точка z смещается от середины колонки вверх или вниз. Соответственно меняются длины дуг ОА и АР₁. Так, амплитуде колонки, пересекаемой дефектом в верхней части соответствует О₁Р₂. Для любых колонок, пересекаемых дефектом, на расстоянии от поверхности, отличающемся на s^-1, точка О на диаграме смещается на целой виток и точки О и Р₁ будут периодически совпадать. Соответствено контраст для таких колонок совпадает. Итак , для колонок с постепенно меняющимся расстоянием от поверхности до дефекта амплитуда периодически меняется. В результате возникает серия полос, соответствующих колонкам с одинаковым расстоянием от поверхности до дефекта ( Рис.21в ). Дефекты упаковки , параллельные плоскости фольги, не дадут полос на изображении, но будут или светлее или темнее окружающего фона. Очевидно, что в нашем рассмотрении картина полос должна быть симметрична относительно участка, на котором дефект пересекает колонку посередине. Если дефект упаковки расположен в фольге переменной толщины, то для колонок, пересекаемых дефектом посередине при изменении толщины Z амплитуда будет периодически меняться. При этом для каждого Z по-прежнему сохраняется система симметричных полос, причем с уменьшением число полос будет уменьшаться. Часто наблюдаемая в толстых фольгах асимметрия контраста на изображениях дефектов упаковки (особенно при s~0) объяснима в рамках динамической теории рассеяния поглощающими кристаллами. Согласно этой теории интенсивность полос зависит от знака 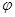. 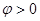Для первая полоса будет светлой, а для 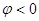- темной. Для темнопольных изображений из-за поглощения дополнительный контраст сохраняется лишь для нижней поверхности фольги. Это позволяет различить следы выхода дефекта упаковки на верхнюю и нижнюю грани фольги, а так же дефекты упаковки внедрения или вычитания. Для иллюстрации возможности определения типа дефекта упаковки рассмотрим конкретный пример .В кубической ГЦК решетке дефект упаковки можно определить вектором смещения u=(а/3)<111>. Судя по характеру контраста на светлопольном изображении 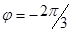.По электронограмме установлено, что антипараллельно электронному лучу направление [ 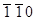]. По положению верхней и нижней кромок дефекта упаковки можно установить, что его плоскость залегания (111).Будем считать, что верхняя часть кристалла закреплена, а нижняя, находящаяся под дефектом, смещена в случае дефекта внедрения в направлении [111] ( см. рис.22). Тогда для отражения 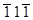, формирующего изображение, судя по контрасту на светлопольном изображении, 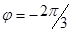. Это соответствует дефекту внедрения. Если бы дефект был типа вычитания , то направление вектора было противоположным: u= 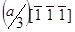и 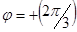для этого отражения.

Рассмотрим теперь плоский дефект, при переходе через который слегка меняется ориентация решетки.Примером такого дефекта может служить когерентная двойниковая граница. Характер контраста в этом случае напоминает полосы от дефектов упаковки и его, обычно называют 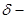контрастом. Учитывая, что вектор s, характеризующий условия дифракции в матрице и двойнике, разный обычно по разные стороны изображения границы (в светлом и темном поле) яркость изображения различна. Кроме того, в отличие от дефектов упаковки в толстых поглощающих фольгах светлопольное изображение имеет асимметричное чередование полос, а темнопольное наоборот – почти симметричное, если экстинкционные длины в верхней и нижней частях фольги равны. Контраст крайних полос при 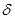-контрасте зависит от знака 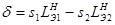, где s_1,2 и 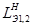-параметры отклонения и экстинкционные длины для создающего контраст отражения Н для верхней (1) и нижней (2) областей фольги. Очевидно, что при 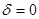контраст исчезает. Для 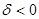первая полоса темная в светлопольном и темная в темнопольном изображениях для верхней части границы и последняя светлая в светлопольном и темная в темнопольном изображении для нижней. Аналогичный характер контраста может проявляться на границе двух магнитных доменов, различие в условиях дифракции которых вызвано магнитострикционным эффектом. Если вектор смещения u (u₁u₂u₃) для двух участков кристалла, разделенных плоской границей, является вектором трансляции в неупорядоченной и не является таковым в упорядо ченной структуре, то поверхность раздела называют антифазной границей. Соответствующий фазовый сдвиг 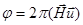. Очевидно, что для отражений, формирующих изображение, разрешенных законом погасаний для неупорядоченной решетки, 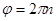( где n =1,2,3..) и в этом случае антифазные границы не создают контраста. Поэтому контраст могут давать только сверхструктурные отражения. Пусть, например, для сверхструктуры CsCl вектор u=(а/2)<111>. Тогда 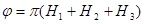. В этом случае отражения, запрещенные законом по гасаний типа 100 или 111 могут давать контраст так как для них 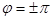. В результате должна возникнуть для наклонной границы картина полос, видная только в темном поле в сверхструктурном отражении. Однако, периодичность полос существенно отличается от периодичности, наблюдаемой для дефектов упаковки. При s=0 периодичность полос на плоских границах типа дефекта упаковки определяется экстинкционной длиной L_Э. Но для слабых сверхструктурных отражений она очень большая, соответственно число полос невелико. Интересная особенность контраста, вызванная различием структурных амплитуд между изображениями двух частей кристалла, представляющих двойник, наблюдается, например, для дофинейских двойников в кварце. 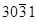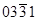Если в формировании изображения происходит когда одновременно действуют рефлексы и , имеющие существенно отличающиеся структурные амплитуды, то яркость изображения двойников, например, в рефлексе 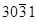существенно отличается.

Статистический ряд распределения и порядок его построения

Архивные данные, содержащие наблюдения за случайными величинами или явлениями, зачастую требуют дальнейшей обработки. Целью подобных действий является их представление в более удобном для восприятия виде. Для этого разработан специальный алгоритм статистической обработки результатов наблюдений.

Первым шагом на пути статистической обработки результатов наблюдений случайных объектов является сбор статистических данных. Простейшей формой записи результатов метеорологических наблюдений служит простой статистический ряд, который обычно оформляется в виде таблицы последовательных записей. Форма такой таблицы в каждом конкретном случае выбирается исходя из удобства первичной записи и последующей обработки результатов наблюдений. В качестве примера простого статистического ряда может служить дневник погоды.

При изучении распределений метеорологических случайных величин приходится прибегать к большому числу наблюдений (обычно несколько сотен случаев). В таких ситуациях выявить характер распределения случайной величины непосредственно из простого статистического ряда наблюдений практически невозможно. Поэтому он подвергается соответствующей обработке. Первым шагом такой обработки является формирование рядов, содержащих только необходимую исследователю информацию.

Следующим шагом является формирование вариационного или ранжированного ряда.Вариационным (ранжированным) статистическим рядом называется ряд, в котором элементы выборки расположены в порядке возрастания: 12,5; 13,2; 13,9; 15,4; 15,4; 15,8. Вариационный ряд, упорядочен по сравнению с простым статистическим рядом, но неудобен для анализа из-за большого количества случаев наблюдения.

Следующим этапом обработки статистических рядов является группирование элементов выборки. При этом члены ряда объединяются в отдельные группы так, чтобы по ним можно было получить подходящие оценки плотности и функции распределения исследуемой случайной величины в виде соответствующих таблиц и графиков. Такая группировка осуществляется следующим образом. Из обрабатываемой совокупности x₁, x₂, ..., x_n выбираются наибольшее и наименьшее значения. Рассчитывается значение

L = x_max - x_min (1)

которое называется размахом выборки.

Затем значение L разбивается на k градаций (интервалов) с указанием значений их границ. Как правило, градации выбираются равными по ширине. В отдельных случаях градации могут выбираться и разной ширины. Следующим этапом является расчет числа попаданий (частоты попадания) наблюдаемых значений величин в границы каждой из выбранных градаций. По полученным для каждой градации частотам вычисляются другие необходимые численности, используемые для описания распределения рассматриваемой случайной величины. Результаты такой обработки простого статистического ряда обычно представляют в виде таблицы, которая называетсястатистическим рядом распределенияслучайной величины.

Определение числа градаций k является важным этапом построения статистических распределений. Если попытаться добиться высокой точности и сделать большое количество градаций, то при небольшой архивной выборке в некоторые градации случайная величина может вообще не попасть, и результаты анализа распределения окажутся статистически незначимыми, т.е. их надежность окажется очень низкой. С другой стороны, при малом числе градаций свойства статистического распределения описываются слишком грубо. Поэтому количество градаций требуется выбирать таким образом, чтобы статистическое распределение было достаточно показательным и, в тоже время, достаточно надежным.

Для одной случайной величины (одномерного распределения) подходящее число градаций k обычно предварительно определяется с использованием неравенства:

k £ 5 lg n, (2)

где n - объем архивной выборки.

Так, например, если объем выборки составляет 100 случаев, то число градаций не может превышать 10. Если же распределение многомерное, то использование формулы (2.2) приведет к статистически незначимым результатам. Считается, что о вероятности можно судить тогда, когда имеется хотя бы 10 случаев попадания в градацию. Исходя из этих соображений, необходимый объем выборки должен определяться по формуле:

n = 10 t, (3)

где t - число возможных сочетаний градаций случайных величин.

Так как t равно произведению градаций всех исследуемых случайных величин, то

n = 10 k₁ k₂ . . . k_n , (4)

где k₁ - количество градаций 1-ой, k₂ - 2-ой случайной величины и т.д..

По выбранному числу градаций k и значению размаха выборки L можно найти минимальную ширину градаций DX:

DХ = L/k (5)

Полученное по этой формуле значение DX округляется в большую сторону. После этой операции выбирается положение левой границы первой градации ряда распределения х₁ из условия: х₁ < х_min и с таким расчетом, чтобы положение правой границы его последней градации х_k+1 соответствовало условию х_k+1 > x_max.

По возможности значения границ градаций следует брать равными целому числу, что упрощает оформление и наглядность при практическом использовании полученного статистического ряда распределения.

В процессе группировки выборки могут быть случаи точного совпадения значений случайной величины с границами градаций. Возникает вопрос: куда отнести данный случай? В такой ситуации можно поступить двумя способами. Во-первых, границы градации можно задавать числами с большим количеством значащих цифр, чем точность измерения членов обрабатываемого ряда. Вторым вариантом решения поставленного вопроса может служить следующий прием. После определения границ градаций принимается условие, что при совпадении значения случайной величины с границей градации, оно относится, например, только к левой из смежных градаций. В этом случае границы градаций можно выражать наиболее удобными числами, включая и целые. После определения количества градаций и их ширины появляется возможность построения рядов дифференциального и интегрального распределений.

Основными численностями, используемыми при построении статистических распределений являются: абсолютная частота, относительная частота, абсолютная плотность, относительная плотность градаций, абсолютная накопленная частота и относительная накопленная частота.

Дата добавления: 2014-07-19; просмотров: 586; Нарушение авторских прав

Мы поможем в написании ваших работ!