
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Устойчивость откосов и склонов
Назначение и содержание диагностических нормативов
Диагностические нормативы служат для количественной оценки технического состояния автомобиля по результатам измерения текущих значений диагностических параметров, а так же для планирования и организации процесса диагностирования.
К важнейшим нормативам относятся:
– начальное (номинальное) значение диагностического параметра SН;
– предельное значение диагностического параметра SП;
– допустимое (упреждающее) значение диагностического параметра SД;
– периодичность диагностирования lд.
Начальное (номинальное) значение диагностического параметра – это значение нового технически исправного объекта.
В эксплуатации SН используется как величина, до которой необходимо довести значение параметра путем восстановительных и регулировочных операций. Начальное значение диагностического параметра обычно задается технической документацией.
Предельное значение диагностического параметра – это значение параметра, при котором дальнейшая эксплуатация объекта становится невозможной или нецелесообразной по технико–экономическим соображениям.
В эксплуатации данный норматив используется для прогнозирования ресурса и для назначения ремонтных операций.
Допустимое (упреждающее) значение параметра является основным диагностическим нормативом при диагностировании, проводимом в рамках планово–предупредительной системе технического обслуживания. Он представляет собой ужесточенную величину предельного норматива, при которой обеспечивается заданный уровень вероятности отказа на предстоящем межконтрольном периоде.
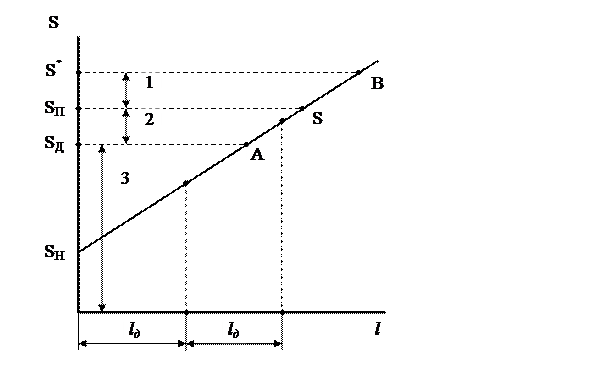
А – профилактика (упреждение неисправности);
Б – неисправность (упреждение отказа);
В – отказ;
1 – зона предотказного состояния;
2 – зона исправной работы (запас исправной работы соответствующей межконтрольному пробегу);
3 – зона работоспособного, исправного состояния.
Для обеспечения условий сравнимости диагностические нормативы относят к определенным скоростным, нагрузочным и тепловым режимам работы объекта.
В зависимости от порядка регламентации диагностические нормативы можно разделить на три группы:
– устанавливаемые техническими регламентами и стандартами;
– рекомендованные предприятиями изготовителями;
– не оговоренными предприятиями изготовителями и стандартами.
Диагностические нормативы первой группы относятся в основном к узлам, влияющим на безопасность движения и экологичность. Как правило, эти параметры отражают основные рабочие процессы механизмов (тормозной путь, выбросы вредных веществ).
Диагностические нормативы второй группы связаны с технологическими допусками структурных параметров на изготовление механизма, с одной стороны и с показателями надежности, долговечности и экономичности, с другой стороны. Следовательно, эти нормативы относятся в основном к структурным параметрам, используемым в качестве диагностических параметров (зазоры в клапанном механизме, углы установки управляемых колес). В процессе эксплуатации эти нормативы могут корректироваться в пределах допуска на структурные параметры.
Существенным отличием нормативов третьей группы является невозможность использования единого норматива для различных условий эксплуатации в силу неоднородности физических процессов работы автомобилей. Например, расход топлива на равнине будет больше чем в горной местности. Поэтому необходима их корректировка для конкретных условий работы автомобиля. Для этого используется ряд методов.
Экономико–вероятностный метод определения диагностического параметра по совокупной реализации диагностических параметров.
Сущность метода заключается в оптимизации допустимого значения диагностического параметра SД и периодичности диагностирования lд по критерию минимума суммарных удельных затрат на ремонт, профилактику и диагностирование.
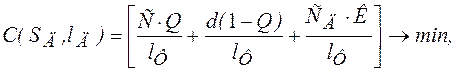
где С – стоимость аварийного ремонта;
d – стоимость профилактики;
СД – стоимость диагностической проверки;
К – среднее число диагностических проверок до восстановления;
lФ – фактический средний ресурс;
Q – суммарная вероятность отказов.
Q, K, lФ – являются функциями установленного допустимого значения параметра SД и установленной периодичности диагностирования LД.
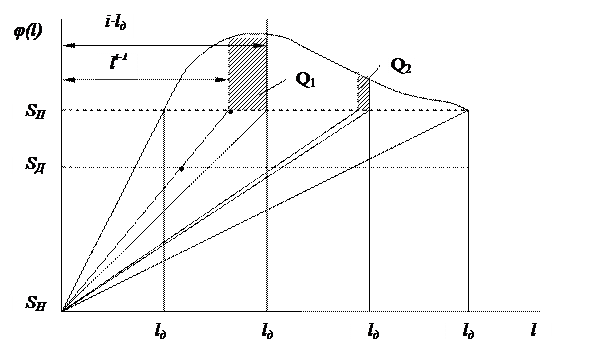
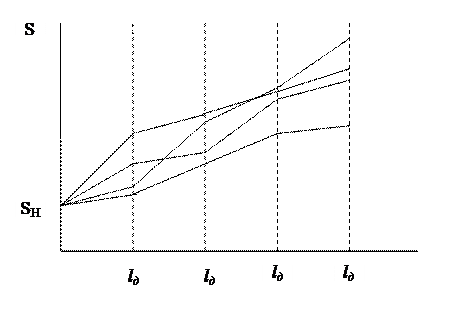
Графически метод можно представить следующим образом.
На рисунке представлены линейные реализации диагностического параметра (S) совокупности автомобилей с рассеиванием скорости их изменения.
Реализации диагностических параметров, величина которых на момент контроля (lД) находится выше допустимого значения прерываются и узлы подвергаются профилактике стоимостью (d). В тоже время часть реализаций за период пробега между диагностированием успевают достигнуть своего предельного значения (SП) и наступает отказ. В этом случае производится аварийный ремонт стоимостью (С).
Из рисунка видно, что заштрихованные площади Q1 и Q2 есть не что иное, как вероятность пропуска отказов на межконтрольном пробеге.
Зная плотность распределения ресурса диагностируемого объекта f(l) можно определить суммарную вероятность отказов.
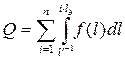
где i – порядковый номер (цикл) диагностирования;
n – последний межконтрольный период в котором могут быть отказы.
Величину li-1 можно определить из подобия прямоугольных треугольников SПАО и SДВО :
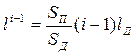
при этом 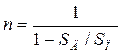
Фактический средний ресурс lФ складывается из двух составляющих. Первая – это ресурс тех элементов, которые отказывают в межконтрольных циклах. Вторая – это ресурс элементов замененных или восстановленных после очередного цикла диагностирования. Тогда фактический ресурс определяется следующим образом:
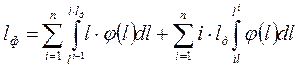 .
.
Следует отметить, что при нелинейных реализациях диагностического параметра:
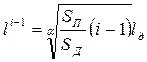

где α – показатель степени определяющий характер изменения параметра.
C>d>Cd
Определение допустимого значения диагностического параметра по его связи со структурным параметром
На основании одновременного изменения структурного параметра X и диагностического параметра S устанавливают вид зависимости 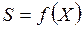 .
.
Вид функции может быть линейной:
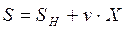 ,
,
где v – чувствительность параметра S к параметру X,
степенной:
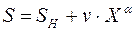 ,
,
где α – показатель степени связи.
Исходя их этих функций определяют допустимое значение диагностического параметра:
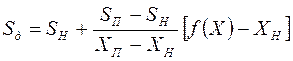 .
.
Следует сказать, что данная методика разработана достаточно глубоко и имеет несколько модефикаций, в том числе и позволяющие учитывать экономические аспекты диагностирования.
Методика определения допустимого значения диагностического параметра по матрице переходных вероятностей.
Метод применяется тогда, когда основное влияние на изменение параметра оказывают переменные эксплуатационные факторы. Корреляционная функция быстро убывает, приращения параметра на отдельных циклах межконтрольной наработки оказываются слабо зависящими один от другого. Иначе говоря, данные об изменении параметра в прошлом дают мало информации о его поведении в будущем. В таких условиях можно прогнозировать вероятности тех или иных приращений параметра за цикл межконтрольной наработки.
При фиксированной периодичности контроля процесс изменения диагностического параметра можно описать в виде конечной дискретной цепи Маркова.
Для этого весь диапазон изменения диагностического параметра делят на m интервалов и считают, что элемент находится в состоянии Пi , если текущее значение диагностического параметра лежит в i - м интервале ( i=1, 2,…, m в порядке уменьшения работоспособности элемента). Для диагностических параметров машин рекомендуется m=5…10. Состояние П0 соответствует номинальным значениям параметров. Кроме того, вводят состояние Пm+1, соответствующее отказу элемента на межконтрольном цикле. Предполагают, что за период межконтрольной наработки состояние элемента с вероятностью qij может изменятся от Пi до Пj.
Поскольку состояния пронумерованы в порядке уменьшения работоспособности, переходы i>j естественно считать недопустимыми (qij=0). Вероятности qi(m+1) соответствуют вероятностям отказа элемента на предстоящей межконтрольной наработке при условии, что в момент контроля он был в состоянии Пi.
На рисунке 2.1 показана схема возможных изменений состояния элемента за один цикл контроля при m=3.
Множество 
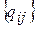 образует исходную матрицу переходных вероятностей:
образует исходную матрицу переходных вероятностей:
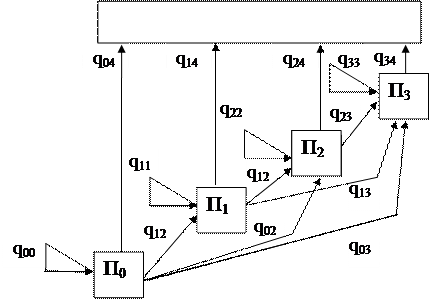 |
Рисунок 1.1-Схемы возможных изменений состояния для марковской модели
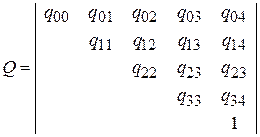 |
При этом q(m+1)(m+1)=1, так как состояние отказа является поглощающим. Экспериментальная оценка вероятностей qij не представляет принципиальных затруднений – достаточно в каждом цикле контроля для всех элементов контрольной группы автомобилей фиксировать квантовые значения диагностического параметра либо факт отказа, если он возник в данном цикле. Переходные вероятности определяются по формуле

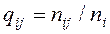 ,
,
где ni – число случаев, когда было зафиксировано состояние 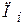
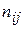 – число случаев перехода за один цикл из состояния
– число случаев перехода за один цикл из состояния 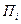 в состояние
в состояние 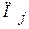 .
.
Путем преобразования матрицы переходных вероятностей можно описать весь бесконечный процесс поддержания работоспособности элемента для всех возможных допускаемых значений квантованного диагностического параметра с целью определения соответствующих уровней суммарных удельных затрат и выбора оптимального допускаемого значения.
Пусть состояние Пl принято в качестве допускаемого. Это означает, что если в момент контроля имеет место состояние с номером i>l , то проводится восстановление элемента: предупредительное обслуживание, если, и аварийный ремонт, если.
При аварийном ремонте (стоимостью А) элемент зачастую заменяют, т.е. переводят в номинальное состояние П0.При техническом обслуживании элемент в простейшем случае также всегда доводят до состояния П0 путём предупредительного ремонта (стоимостью С0<А).В более общем случае при ТО и ТР проводят также частичное восстановление(регулирование) агрегата до некоторого фиксированного значения Пk (стоимостью Сk< C0). При этом наряду с оптимизацией допускаемого состояния требуется одновременно оптимизировать стратегию проведения предупредительного обслуживания.
Преобразованная матрица Р отличается от исходной Q. Последняя строка, соответствующая состоянию Пm+1, заменена первой строкой матрицы, соответствующей состоянию П0; предпоследние строки, соответствующие состояниям Пl+1; Пl+2; …; Пm, заменены либо первой строкой матрицы Q
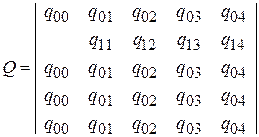 |
для полного предупредительного восстановления (ремонта), либо (k+1)-й строкой, соответствуюющей состоянию Пk для частичного профилактического восстановления (регулирования):
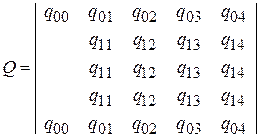 |
Описанное преобразование и расчёт оптимального допускаемого значения параметра технического состояния элемента выполняют в следующей последовательности.
В качестве исходных данных для расчёта используют выборку N пар значений диагностического параметра, соответствующих двум возможным посследовательным моментам коннтроля. При появлениии отказа элемента в цикле межконтрольной наработки фиксируют только одно значение параметра (в начале цикла) и отмечают факт отказа.
Разбивают диапазон значений диагностического параметра на m уровней и оценивают переходные вероятности 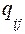 Для этого последовательно выбирают все пары с
Для этого последовательно выбирают все пары с 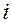 - м начальным состоянием (общее число таких пар
- м начальным состоянием (общее число таких пар 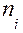 ) . Затем из этих пар выбираются пары с
) . Затем из этих пар выбираются пары с 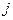 - м конечным состоянием (их число
- м конечным состоянием (их число 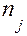 ). Оценкой вероятности
). Оценкой вероятности  является отношение
является отношение
 =
= 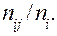
Число уровней квантования лимитируется двумя факторами: разрешающей способностью диагностического оборудования и ограниченным объемом данных при оценке переходных вероятностей. При малом объеме данных погрешность этой оценки может быть недопустимо большой. Для количественного определения погрешности применяют методы построения доверительных интервалов при оценке вероятности по частоте. В зависимости от величины погрешности может оказаться целесообразным скорректировать число уровней квантования (с соответствующим пересчетом переходных вероятностей). Для обеспечения приемлемой погрешности на практике рекомендуется в каждом интервале квантования иметь не менее 40 значений параметра ( 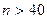 ).
). 
Составляют исходную матрицу переходных вероятностей
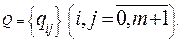
По результатам технико-экономического анализа определяют средние издержки: А – по устранению последствий отказа,  - связанные с полным предупредительным восстановлением параметра до номинального значения
- связанные с полным предупредительным восстановлением параметра до номинального значения 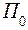 , и
, и 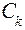 - связанные с предупредительным частичным восстановлением параметра до значения
- связанные с предупредительным частичным восстановлением параметра до значения 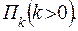
В общем случае составляют множество преобразованных матриц
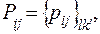 где
где 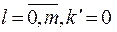 или
или 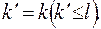
Каждую преобразованную матрицу 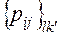 , определяют следующим образом:
, определяют следующим образом:
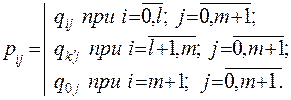
Здесь 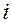 - номер строки;
- номер строки; 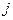 - номер столбца.
- номер столбца.
Для каждой матрицы 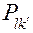 составляют и решают (относительно
составляют и решают (относительно 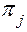 ) систему уравнений
) систему уравнений

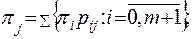
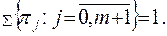
Здесь 
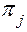 – вероятность того, что элемент в произвольный момент контроля находится в состоянии
– вероятность того, что элемент в произвольный момент контроля находится в состоянии 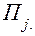
Для каждой матрицы 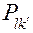 и полученного для нее вектора вероятностей
и полученного для нее вектора вероятностей 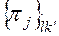 вычисляют средние удельные затраты
вычисляют средние удельные затраты

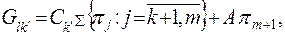
где 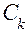 – средние издержки профилактического восстановления (полного при
– средние издержки профилактического восстановления (полного при 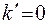 и частичного при
и частичного при 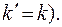
Выбирают матрицу 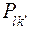 , для которой значение
, для которой значение 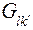 минимально. Эта матрица определяет оптимальную стратегию обслуживания агрегата, т.е. оптимальное допускаемое состояние
минимально. Эта матрица определяет оптимальную стратегию обслуживания агрегата, т.е. оптимальное допускаемое состояние 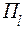 и оптимальный уровень восстановления
и оптимальный уровень восстановления 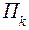 при профилактике.
при профилактике.
Типичными диагностическими параметрами, для которых целесообразно применять данную методику, являются, например, люфты трансмиссии. Они имеют характерную вероятностную связь с отказом, а их реализации по пробегу отличаются значительными колебаниями скорости увеличения параметра на отдельных участках контроля.
Статистический метод корректировки диагностических нормативов.
Данная методика предусматривает объективное назначение диагностических нормативов на основе статистического анализа распределения значений диагностических параметров у группы подконтрольных автомобилей, находящихся в характерных условиях эксплуатации.
Сущность методики состоит в следующем. Рассматривается разовая выборка N значений диагностического параметра, измеренных у представительной совокупности объектов диагностирования (как исправных, так и неисправных). При этом предполагается, что величины, соответствующие неисправному состоянию, будут подчиняться другой закономерности распределения, нежели величины, соответствующие исправному состоянию. Выделив из общей совокупности функцию распределения f(S)значений параметра для исправного состояния объекта, область допустимых в эксплуатации значений диагностического параметра можно ограничить некоторым предельным рассеиванием относительного номинального (наилучшего) значения параметра. Полученные таким образом пределы и будут являться нормативными значениями диагностических параметров.
При этом необходимо иметь в виду, что предельное значение диагностического параметра для совокупности механизмов также имеет естественное рассеивание, и чем больше параметр отличается от своего номинального значения, тем вероятнее становится неисправное состояние. В силу этого на граничных областях рассеивания, аппроксимируемого теоретическим законом, одни и те же значения диагностического параметра могут соответствовать для различных механизмов как исправному, так и неисправному состоянию. Поэтому уровень вероятности, с которым ограничивают рассеивание при определении нормативного показателя, необходимо выбирать с учетом ошибок первого и второго рода, возможных при диагностировании.
Ошибка первого рода (a) "ложная неисправность" состоит в признании механизма неисправным в тот момент, когда он является исправным; ошибка второго рода (b) "пропуск неисправности" – признание механизма исправным при его неисправном фактическом состоянии. Исходя из практического опыта, можно считать, что все значения диагностического параметра, находящиеся в пределах рассеивания А0,85 (ограниченного уровнем вероятности Р=0,85), соответствуют исправному состоянию, ошибка второго рода при этом будет минимальна; значения параметра, выходящие за пределы рассеивания А0,95 (ограниченного уровнем вероятности Р= 0,95), соответствуют неисправному состоянию и минимальному значению ошибки первого рода (рисунок 1). Значения параметра внутри диапазона А0,85 – А0,95 будет соответствовать как исправному, так и неисправному состоянию, при этом вероятности обоих состояний можно считать одинаковыми, т.е. a=b= 0,05.
Поскольку для наиболее ответственных механизмов ошибки второго рода при постановке диагноза должны быть минимальными, то нормативные значения должны ограничиваться более жестким, 85% – рассеиванием А0,85, при котором будут иметь место досрочные ремонты и регулировки. Для остальных механизмов рядового использования технические воздействия желательно проводить при явно выраженной неисправности, поскольку стоимость устранения аварийных отказов сопоставима с затратами на профилактику. Поэтому ошибка первого рода при постановке диагноза должна быть минимальная, и нормативные значения необходимо ограничивать менее жестким, 95% рассеиванием А0,95. При таком подходе максимальная ошибка диагноза не превысит 5% и будет приводить к наилучшему для рассматриваемых условий исходу, удовлетворяя в целом требованиям эксплуатации.
В зависимости от закономерностей изменения диагностического параметра его рассеивание может быть ограничено с одной или с двух сторон. При одностороннем ограничении номинальным значением диагностического параметра Sн является наилучшая его величина (наименьший расход топлива, вибрация, скорость изнашивания; наибольшая мощность, к.п.д. и т.д.); она не должна исключаться из интервала. При двухстороннем ограничении номинальное значение Sн находится внутри интервала.
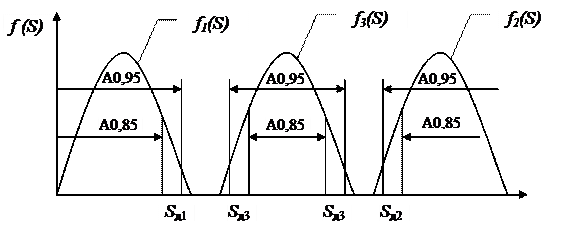
Рисунок 2.1. – Определение нормативного показателя по теоретическому закону распределения диагностического параметра для исправного состояния механизма при различных видах ограничений.
Основная трудность при подборе теоретического распределения f(S) связана с выделением из всей совокупности измеренных в эксплуатации параметров той части опытных данных, которая соответствует исправному состоянию. Для этого приходится проводить несколько последовательных расчетов при изменяющихся границах выборки Smin… Smax , включающих в себя номинальное значение Sн. Параметры теоретического закона рассчитываются вероятностными методами по гистограмме распределения, и закон считается подобранным, если вероятность согласования его с гистограммой, определенная по критерию 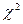 Пирсона в границах Smin… Smax , будет наибольшей, но не ниже 0,3.
Пирсона в границах Smin… Smax , будет наибольшей, но не ниже 0,3.
Приближенное значение интервала DS для построения гистограммы определяют формулой Стеджерса:
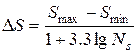

где NS – количество данных, находящихся в интервале Smin… Smax.
Так как в условиях неопределенности можно считать вероятности исправного и неисправного состояний одинаковыми, то объем выборки для определения нормативного показателя должен составить не менее Ns=(20–30)2 автомобилей характерных возрастных групп и условий эксплуатации. При этом согласно практическому опыту, в первую очередь необходимо выделять в отдельные группы новые, изношенные и прошедшие капитальный ремонт агрегаты и узлы автомобиля.
1. Значения диагностического параметра из выборки, приведенной в задании, расположить в порядке возрастания и выбрать предварительные границы выборки Smin… Smax, включающие начальное значение Sн и значения, соответствующие наибольшей плотности выборки, т.е. наиболее часто встречающиеся значения параметра.
2.Для выборки, находящейся в диапазоне Smin… Smax по формуле Стеджерса (2.1) определить интервал DS и построить гистограмму распределения.
3. Определить среднее значение выборки Sср и среднеквадратическое отклонение 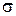 .
.
4. По полученным значениям Sср и 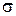 определить теоретические законы распределения ¦(S) – нормальный или гамма – распределение - и найти по критерию c2 Пирсона вероятность его согласования
определить теоретические законы распределения ¦(S) – нормальный или гамма – распределение - и найти по критерию c2 Пирсона вероятность его согласования 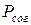 с гистограммой в диапазоне Smin… Smax (для дальнейшего анализа принимается закон, для которого вероятность согласования будет наибольшей).
с гистограммой в диапазоне Smin… Smax (для дальнейшего анализа принимается закон, для которого вероятность согласования будет наибольшей).
5. Произвести последовательное изменение границ выборки таким образом, чтобы вероятность согласования вновь рассчитанных теоретических законов повысилась. При этом границы выборки могут, как сужаться, так и расширяться, а также смещаться вправо или влево, но обязательно должны включать в себя начальное значение параметра Sн. Закон считается подобранным при наибольшей вероятности согласования, но не меньшей 0,3.
6. Определить, исходя из физической природы параметра и вида гистограммы, вид его ограничения (снизу, сверху или двухсторонний) и принять допустимый уровень вероятности рассеивания (А0,85 или А0,95). Для диагностических параметров узлов, агрегатов и систем, влияющих на безопасность движения, принимают более жесткое 85%-ограничение (А0,85), чем для менее ответственных, для которых принимают 95% - ограничение (А0,95).
Рассчитать допустимое значение диагностического параметра SД, исходя из следующего:
– одностороннее ограничение сверху
при А0,85 норматив Sд = Sср + s;
при А0,95 норматив Sд = Sср + 1,7s;
– одностороннее ограничение снизу
при А0,85 норматив Sд = Sср – s;
при А0,95 норматив Sд = Sср – 1,7s;
– двухстороннее ограничение
при А0,85 норматив Sд = Sср ± 1,5s;
при А0,95 норматив Sд = Sср ± 2s.
Устойчивость откосов и склонов
Общие положения
Откосом называется искусственно созданная поверхность, ограничивающая природный грунтовый массив, выемку или насыпь. Откосы образуются при возведении различного рода насыпей (дорожное полотно, дамбы, земляные плотины и. т.д.), выемок (котлованы, траншеи, каналы, карьеры и .п.) или при перепрофилировании территорий.
Склоном называется откос, образованный природным путем и ограничивающий массив грунта естественного сложения.
При неблагоприятном сочетании разнообразных факторов массив грунтов, ограниченный откосом или склоном, может перейти в неравновесное состояние и потерять устойчивость.
Основными причинами потери устойчивости откосов и склонов являются:
1. устройство недопустимо крутого откоса или подрезка склона, находящегося в состоянии, близком к предельному;
2. увеличение внешней нагрузки (возведение сооружений, складирование материалов на откосе или вблизи его бровки);
3. изменение внутренних сил (увеличение удельного веса грунта при возрастании его влажности или, напротив, влияние взвешивающего давления воды на грунты);
4. неправильное назначение расчетных характеристик прочности грунта или снижение его сопротивления сдвигу за счет, например повышения влажности;
5. проявление гидродинамического давления, сейсмических сил, различного рода динамических воздействий (движение транспорта, забивка свай и. т.п.).
Инженерные методы расчета устойчивости откосов и склонов
В проектной практике применяются инженерные методы расчета устойчивости, содержащие различного рода упрощающие предположения. Наиболее распространенный из них – метод круглоцилиндрических поверхностей скольжения, относящий к схеме плоской задачи.
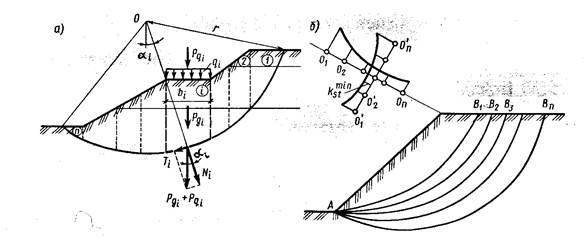
Рис. 1. Схема к расчету устойчивости откосов методом круглоцилиндрических поверхностей скольжения: а) – расчетная схема; б) – определение положения наиболее опасной поверхности скольжения; 1, 2, … - номера элементов.
Этот метод был впервые применен К. Петерсоном в 1916 г. для расчета устойчивости откосов (тогда и долгое время назывался методом шведского геотехнического общества).
Рассмотрим широко используемую модификацию этого метода. Предположим, что потеря устойчивости откоса или склона, представленного на рис. 1, а, может произойти в результате вращения отсека грунтового массива относительно некоторого центра  . Поверхность скольжения в этом случае будет представлена дугой окружности с радиусом r и центром в точке
. Поверхность скольжения в этом случае будет представлена дугой окружности с радиусом r и центром в точке  . Смещающийся массив рассматривается как недеформируемый отсек, все точки которого участвуют в общем движении. Коэффициент устойчивости принимается в виде
. Смещающийся массив рассматривается как недеформируемый отсек, все точки которого участвуют в общем движении. Коэффициент устойчивости принимается в виде
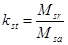 , (1)
, (1)
где 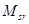 и
и 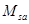 - моменты относительно центра вращения
- моменты относительно центра вращения  всех сил, соответственно удерживающих и смещающих отсек.
всех сил, соответственно удерживающих и смещающих отсек.
Для определения входящих в формулу (1) моментов отсек грунтового массива разбивается вертикальными линиями на отдельные элементы. Характер разбивки назначается с учетом неоднородности грунта отсека и профиля склона так, чтобы в пределах отрезка дуги скольжения основания каждого i-го элемента прочностные характеристики грунта j и с были постоянными. Вычисляются силы, действующие на каждый элемент: вес грунта в объеме элемента 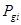 и равнодействующая нагрузки на его поверхность
и равнодействующая нагрузки на его поверхность 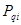 . При необходимости могут быть также учтены и другие воздействия (фильтрационные, сейсмические силы и т.д.). Равнодействующие сил
. При необходимости могут быть также учтены и другие воздействия (фильтрационные, сейсмические силы и т.д.). Равнодействующие сил 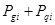 считаются приложенными к основанию элемента и раскладываются на нормальную
считаются приложенными к основанию элемента и раскладываются на нормальную 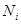 и касательную
и касательную 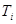 составляющие к дуге скольжения в точке их приложения. Тогда
составляющие к дуге скольжения в точке их приложения. Тогда
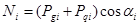 ;
; 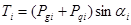
 (2)
(2)
Соответственно момент сил, вращающих отсек вокруг 0, определился как
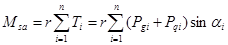 (3)
(3)
где п – число элементов в отсеке.
Принимается, что удерживающие силы в пределах основания каждого элемента 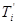 обусловливаются сопротивлением сдвигу за счет внутреннего трения и сцепления грунта. Тогда с учетом выражения для закона кулона
обусловливаются сопротивлением сдвигу за счет внутреннего трения и сцепления грунта. Тогда с учетом выражения для закона кулона 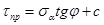 можно записать
можно записать
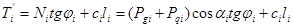 , (4)
, (4)
где 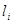 - длина дуги основания i-го элемента, определяемая как
- длина дуги основания i-го элемента, определяемая как 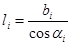 . Здесь
. Здесь 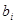 - ширина элемента)
- ширина элемента)
Отсюда момент сил, удерживающих отсек, будет иметь вид
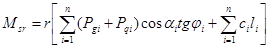 . (5)
. (5)
Учитывая формулу (1), окончательно получим
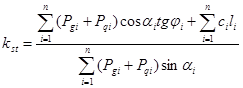 . (6)
. (6)
При 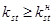 устойчивость отсека массива грунта относительно выбранного центра вращения 0 считается обеспеченной. Основная сложность при практических расчетах заключается в том, что положение центра вращения 0 и выбор радиуса r, соответствующие наиболее опасному случаю, неизвестны. Поэтому обычно проводится серия таких расчетов при различных положениях центров вращения и значениях r. Чаще всего наиболее опасная поверхность скольжения проходит через нижнюю точку откоса или склона. Однако если в основании залегают слабые грунты с относительно низкими значениями прочностных характеристик j и с, то это условие может не выполняться.
устойчивость отсека массива грунта относительно выбранного центра вращения 0 считается обеспеченной. Основная сложность при практических расчетах заключается в том, что положение центра вращения 0 и выбор радиуса r, соответствующие наиболее опасному случаю, неизвестны. Поэтому обычно проводится серия таких расчетов при различных положениях центров вращения и значениях r. Чаще всего наиболее опасная поверхность скольжения проходит через нижнюю точку откоса или склона. Однако если в основании залегают слабые грунты с относительно низкими значениями прочностных характеристик j и с, то это условие может не выполняться.
Один из приемов нахождения наиболее опасного положения поверхности скольжения заключается в следующем. Задавясь координатами центров вращения 01, 02, …, 0n на некоторой прямой, определяют коэффициенты устойчивости 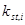 для соответствующих поверхностей скольжения и строят эпюру значений этих коэффициентов (рис.1,б). Через точку 0min, соответствующую минимальному коэффициенту устойчивости, проводят по нормали второй отрезок прямой и, располагая на нем новые центры вращения
для соответствующих поверхностей скольжения и строят эпюру значений этих коэффициентов (рис.1,б). Через точку 0min, соответствующую минимальному коэффициенту устойчивости, проводят по нормали второй отрезок прямой и, располагая на нем новые центры вращения 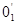 ,
, 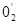 , …,
, …, 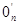 вновь оценивают минимальное значение коэффициента устойчивости. Тогда
вновь оценивают минимальное значение коэффициента устойчивости. Тогда 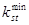 и определит положение наиболее опасной поверхности скольжения. При
и определит положение наиболее опасной поверхности скольжения. При 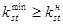 устойчивость откоса или склона будет обеспечена.
устойчивость откоса или склона будет обеспечена.
Мероприятия по повышению устойчивости откосов и склонов.
Одним из наиболее эффективных способов повышения устойчивости откосов и склонов является их выполаживание или создание уступчатого профиля с образованием горизонтальных площадок (берм) по высоте откоса. Однако это всегда связано с увеличением объемов земляных работ. При относительно небольшой высоте откосов может оказаться эффективной пригрузка подошвы в его низовой части или устройство подпорной стенки, поддерживающей откос. Положительную роль также играют закрепление поверхности откоса одерновкой, мощением камнем, укладкой бетонных или железобетонных плит.
Важнейшим мероприятием является регулирование гидрогеологического режима откоса или склона. С этой целью сток поверхностных вод перехватывается устройством нагорных канав, отведением воды с берм. Подземные воды, высачивающиеся на поверхности откоса или склона, перехватываются дренажными устройствами с отведением вод в специальную ливнесточную сеть.
При необходимости разрабатываются сложные конструктивные мероприятия типа прорезания потенциально неустойчивого массива грунтов системой забивных или набивных свай, вертикальных шахт и горизонтальных штолен, заполненных бетоном и входящих в подстилающие неподвижные части массива. Используется также анкерное закрепление неустойчивых объемов грунта, часто во взаимодействии с подпорными стенками или свайными конструкциями.
| <== предыдущая страница | | | следующая страница ==> |
| Диагностические нормативы и методы и определения | | | АРХИТЕКТУРА БЕЛАРУСИ ПЕРИОДА ГОСПОДСТВА ФЕОДАЛЬНО БАРЩИННОЙ СИСТЕМЫ (ВТОРАЯ ПОЛОВИНА XVII—XVIII в.) |
Дата добавления: 2014-07-30; просмотров: 562; Нарушение авторских прав

Мы поможем в написании ваших работ!