Электрический диполь

1.2.1. Поле электрического диполя

Кроме не связанных между собой зарядов – свободные заряды, могут быть и связанные между собой заряды.

Система из двух одинаковых по модулю зарядов разного знака, находящихся на расстоянии друг от друга на расстоянии l друг от друга, называется электрическим диполем.

Такая система создает в пространстве электрическое поле. Оно обладает осевой симметрией, и ось симметрии есть прямая, проходящая через оба заряда, положительный q₊ и отрицательный q_–. Пусть начало координат находится в центре диполя (сердцевина между зарядами), тогда потенциал φ электрического поля в т. r, создаваемого двумя электрическими зарядами, будет:

,

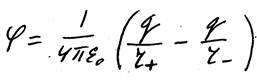
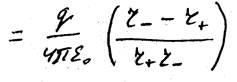где r₊ и r_– – расстояния от т. r до положительного и отрицательного зарядов, соответственно.

Если расстояние от центра диполя до т. r значительно больше расстояния между зарядами l |r| >>l , то φ примерно равно:

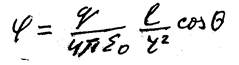
Величину P , равную P= ql – называют электрическим моментом диполя (здесь q = q₊) – это вектор, направленный от отрицательного заряда к положительному, а его начало совпадает с центром диполя. Тогда:

,

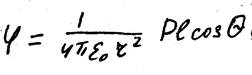где Θ – угол между вектором P и радиус–вектором точки r.

Найдем напряженность электрического поля E в т. r, используя связь между напряженностью Eи потенциалом φ электрического поля в т. r E= - grad φ или

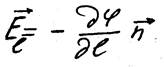,здесь E_l – проекция вектора напряженности электрического поля E на направление перемещения 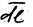, а n -единичный вектор в направлении перемещения.

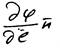– производная по направлению перемещения .

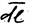В полярной системе координат проекции векторов E_r и E_Θ равны:

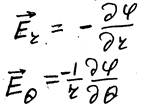
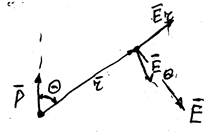
Подставляя в них значение для потенциала φ электрического поля диполя в т. rполучим для компонентE_r и E_Θ:

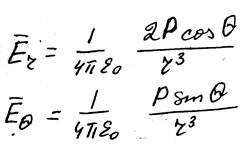
Для модуля вектора E будем иметь:

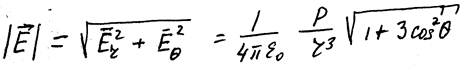
В частности, при Θ = 0, электрическое поле |E| = E_|| равно

,

а при Θ = π/2

Таким образом, при одном и том же r (на одном и том же расстоянии от диполя) поле на оси диполя E_|| в 2 раза больше поля E_┴ .

1.2.2. Силы, действующие на диполь в электрическом поле

а) Результирующая сила F, действующая на диполь со стороны внешнего электрического поля E, создаваемого сторонними зарядами, равна векторной сумме сил, действующих на отдельные заряды диполя, и равна:

,

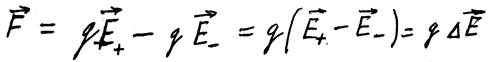где E₊ и E_– – вектора напряженности электрических полей в т. нахождения положительного q₊ и отрицательного q_– зарядов диполя, соответственно, а

ΔE = (E₊ – E_–) – есть приращение поля E на длине l (расстояние между зарядами диполя) вдоль направления вектора P электрического момента диполя (от q_– к q₊).

Т. к. расстояние l между зарядами диполя мало, то ΔE = (E₊ – E_–) = ΔE*l/l = 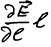(мы ΔE помножили и разделили на малое значение l, эквивалентное Δl и отношение ΔE/Δl при Δl → 0 заменили на частную производную 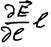(поля E по направлению l )) и тогда

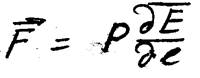
здесь 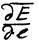– есть производная по направлению, она не совпадает по направлению ни с вектором E, ни с вектором l, т.е. P. Таким образом, видно, что простота формулы обманчива.

В однородном электрическом поле, т. е. поле E не зависит от координат, производная 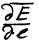= 0 и сила F = 0.

б) Наряду с результирующей силой F со стороны электрического поля на диполь действует момент сил M, стремящийся развернуть диполь (его электрический момент P) по направлению поля E. Его величина равна:

M =[r₊F₊]+ [r_–F_–],

где F₊ = qE₊ , а F_– = –qE_– – силы, действующие на положительный и отрицательный заряды диполя со стороны электрических полей E₊ и E_– в точках нахождения этих зарядов, соответственно и тогда для M можно записать:

M =q([r₊ E₊]– [r_– E_–]

При малом l можно положить E₊ ≈ E_– = Е в центре диполя и тогда:

M =q([(r₊– r_–)E]

Т.к. r₊– r_–= l, то M=q[lE]= [PE]

M= [PE]

Таким образом, в неоднородном электрическом поле диполь будет стремиться: а) повернуться по направлению поля E(стремится к P↑↑Eи

б) переместиться в сторону, где модуль поля |E| максимален.

1.2.3. Энергия диполя в электрическом поле

Энергия W точечного заряда q в электрическом поле равна W = qφ, где φ – потенциал поля E других зарядов в точке нахождения заряда q. Тогда энергия диполя в этом поле E будет:

W = q₊φ₊ + q_–φ_– = q(φ₊– φ_–),

где φ₊и φ_– – потенциалы поля E в т. положительного и отрицательного зарядов диполя, соответственно.

С точностью до величин второго порядка малости можно записать:

,

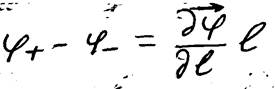где 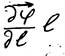– производная от φ по направлению l↑↑P. Эта производная равна (минус) –E_l – составляющей вектора E на направление l или P в точке нахождения диполя и тогда:

W = –PE

Дата добавления: 2014-07-30; просмотров: 479; Нарушение авторских прав

Мы поможем в написании ваших работ!