Оценка шумов квантования

Оценка шумов при равномерном квантовании. Пусть плотность вероятности распределения мгновенных значений входного сигнала описывается функцией w(u_вх) и его квантование осуществляется в пределах от -U₀ до +U₀ (рис.5.1а). Этот диапазон разбит на М шагов квантования, каждый из которых лежит в пределах от u_i - d_i /2 до u_i + d_i /2.

Вероятность появления сигнала с уровнем, лежащем в переделах i-го шага квантования равна

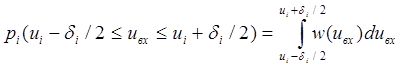. ( 3 )

Поскольку шаг квантования мал по сравнению с диапазоном изменения входного сигнала, эта вероятность может быть принята равной

p_i (u_i - d_i / 2 £ u_i £ u_i + d_i / 2) = w( u_i )d_i ( 4 )

В последней формуле w(u_i ) - плотность вероятности величины напряжения сигнала в середине рассматриваемого интервала.

Мгновенная мощность шума квантования, развиваемая на единичном сопротивлении, равна квадрату ошибки квантования для данного шага квантования:

,

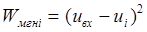а мощность шума квантования, возникающего при квантовании сигналов, лежащих в пределах i-го шага квантования, соответствует

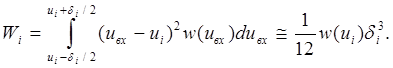( 5 )

С учетом выражений (4) и (5) имеем

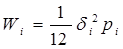. ( 6 )

Мощность полного шума квантования равна сумме составляющих от каждого шага

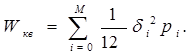( 7 )

При равномерной шкале квантования d_i =d , 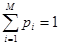и, следовательно,

W_кв = 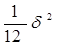. ( 8 )

Из (8) очевидно, что при равномерной шкале квантования мощность шумов квантования не зависит от уровня квантуемого сигнала и определяется только шагом квантования.

Шумы квантования действуют только одновременно с передачей сигнала: есть сигнал - есть шумы квантования, нет сигнала - нет шумов квантования. Поэтому влияние шумов квантования на качество передачи удобно оценивать отношением сигнал/шум квантования (ОСШК) равным

h = W_c/W_кв ( 9 )

или в логарифмических единицах (дБ) , оно рассматривается как защищенность сигнала от шума квантования

A_кв=10lg(W_c/W_кв), ( 10 )

здесь W_c - мощность полезного сигнала.

При известном динамическом диапазоне квантуемого сигнала шаг квантования d определяет число уровней квантования М и, следовательно, число элементов (или разрядность) кода m, необходимого для последующего кодирования квантованных отсчетов сигнала с целью формирования двоичного цифрового сигнала.

Сигналы, поступающие на вход квантующего устройства от различных источников, могут значительно различаться по мощности, динамическому диапазону. Например, из-за различия микрофонов, вида и длины абонентских линий, особенностей говорящих параметры телефонных сигналов значительно разняться между собой. Поскольку параметры квантующего устройства и в последующем устройства кодирования остаются неизменными, то шаг квантования следует выбирать исходя из того, чтобы шумы квантования не превышали допустимого значения для минимальных по мощности сигналов. В то же время во избежание значительных шумов ограничения порог ограничения U₀ (рис.5.1а) должен выбираться исходя из параметров максимального по уровню входного сигнала.

Примем, что порог ограничения выбран в k раз больше, чем среднеквадратическое значение напряжения (s_смакс) максимального по уровню входного сигнала, т.е.

U₀ = ks_смакс. ( 11 )

Если шкала квантования строится таким образом, чтобы шумы ограничения не возникали, то величина U₀ должна совпадать с пиковым значением сигнала. В этом случае коэффициент k показывает, во сколько раз пиковое значение сигнала больше его среднеквадратического значения, и численно совпадает с пик-фактором сигнала. В общем случае коэффициент k устанавливает связь между значениями параметров сигнала и шкалы квантования. С его использованием между U₀ , d и числом уровней квантования М может быть установлена следующая связь:

при квантовании двуполярных сигналов:

М = 2 êU₀ ç / d + 1 » 2 çU₀ ç/ d , (12 )

при квантовании однополярных сигналов:

М = çU₀ ç/ d. ( 13 )

Подставив выражения (11) - (13) в формулу (8), получим иное представление для оценки шума квантования. В случае двухполярного сигнала имеем:

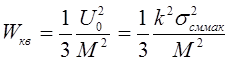. ( 14 )

В случае однополярного сигнала получим:

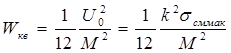. ( 15 )

Мощность полезного сигнала равна его дисперсии, т.е.

W_c = 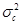, ( 16 )

поэтому и квадрат среднеквадратического значения s²_смакс представляет мощность наибольшего входного сигнала, т.е. 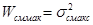. Используя (9), (10) и (14), (16), находим ОСШК:

для двуполярных сигналов:

h = 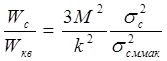( 17 )

или защищенность ( в дБ ):

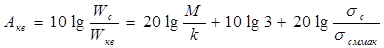; ( 18 )

для однополярных сигналов:

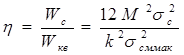( 19 )

или

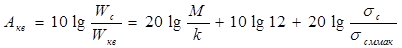. ( 20 )

При m - разрядном кодировании 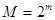. Подставив это значение в формулы (18) и (20), получим значения защищенности от шумов квантования для двуполярного сигнала:

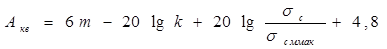( 21 )

и для однополярного сигнала:

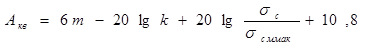. ( 22 )

При квантовании сигнала от одного источника, когда s_с = s_смакс, защищенность от шумов квантования определится по формулам:

А_кв = 6m - 20 lg k + 4,8 ( 23 )

для двуполярных сигналов и

А_кв = 6m - 20 lg k + 10,8 ( 24 )

для однополярных сигналов.

Последние формулы показывают, что при равномерном квантовании защищенность А_кв увеличивается на 6 дБ с возрастанием разрядов в кодовой группе на каждую единицу и при s_c < U₀ она растет прямо пропорционально уровню сигнала , см. формулы (5.21) и (5.22). Так , при переходе от восьмиразрядного к девятиразрядному коду защищенность от шумов квантования А_кв увеличивается на 6 дБ, но при этом требуемая скорость передачи возрастает на 12,5%, что не всегда является приемлемым.

Воспользуемся полученными формулами для оценки защищенности от шумов квантования для различных сигналов.

Гармонический сигнал. Величину порога ограничения U₀ принять равным амплитуде сигнала U_макс. Тогда коэффициент k = U_макс / s_c = 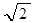, а защищенность от шумов квантования согласно (23) будет равна

А_кв1 = 6m -20lg 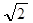+ 4,8 = 6m + 1,8. ( 25 )

Речевой сигнал. Плотность вероятности распределения мгновенных значений речевого сигнала для большинства практических задач принято представлять экспоненциальным законом и в случае кодирования одиночного сигнала принимают значение коэффициента k=5, при котором вероятность появления шумов ограничения не превышает 10^-4. Подставив значение k в (23),получим

А_кв2 = 6m - 20lg5 + 4,8 = 6m - 9,2 ( 26 )

Речевой сигнал, поступающий от разных источников. В этом случае расчет защищенности следует производить по формуле (21). С учетом (26) имеем

А_кв3 = 6m - 9,2 + 20lg(s_c / s_смакс). ( 27 )

Распределение средних мощностей телефонных сигналов от различных источников соответствует нормальному закону со среднеквадратическим отклонением s_с = 3,5...5,5 дБ. При этом с вероятностью р=0,997 значения случайной величины не выходят за пределы ± 3s_с, что при s_с=5,5 дБ составляет ± 16,5 дБ. С учетом сказанного защищенность от шумов квантования для самых слабых сигналов будет равна

А_кв3 = 6m - 42,2. ( 28 )

Многоканальный групповой телефонный сигнал. В этом случае принимают k = 4 и из (23) находим защищенность от шумов квантования равную

А_кв4 = 6m - 7,2. ( 29 )

Многоканальный групповой телефонный сигнал имеет нормальное распределение мгновенных значений и при k=4 вероятность появления шумов ограничения не превышает р = 10^-4.

Телевизионный сигнал. Поскольку телевизионный сигнал является однополярным и при k = 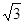(для этой величины вероятность появления шумов ограничения весьма мала) защищенность от шумов квантования находится по формуле (24)

А_кв5 = 6m - 20lg 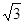+ 10,8 » 6 (m + 1). ( 30 )

Выражения (21) и (22) показывают, что защищенность от шумов квантования непостоянно для сигналов различного уровня. Оно минимально для слабых сигналов и растет с увеличением отношения s_с/s_смакс. При s_с = s_смакс защищенность от шумов квантования максимальна. При s_с >s_смакс возрастает вероятность появления шумов ограничения и защищенность от суммарного влияния шумов квантования и ограничения уменьшается. Рассчитаем мощность шума ограничения, предполагая, что квантованию подвергается речевой сигнал.

Мгновенное значение шума ограничения x_огр= u - U₀ и его мощность связаны соотношением

W_огр = 2 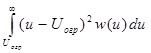. ( 31 )

Здесь 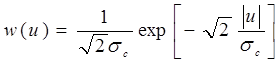- плотность вероятности распределения мгновенных значений речевого сигнала. Подставив формулу для w(u) в (31) и выполнив некоторые преобразования , получим

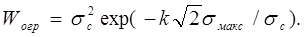( 32 )

Защищенность от шумов ограничения будет равна

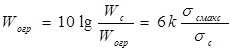. ( 33 )

Отношение W_c / W_огр растет с увеличением k, что естественно, поскольку при этом растет порог ограничения U₀ и, следовательно, уменьшается вероятность его превышения. Поскольку шумы квантования и ограничения независимы, то общий шум, возникающий при квантовании, равен сумме этих шумов, т.е.

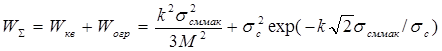. ( 34 )

Результирующее значение отношения сигнал/шум определится, следовательно, по формуле

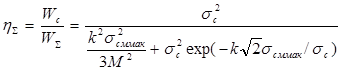. ( 35 )

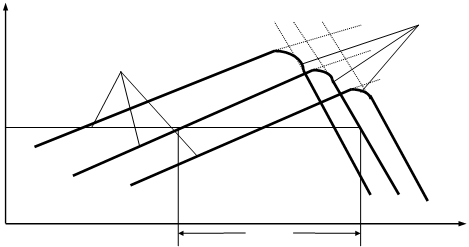
На рис. 2 приведена зависимость этого отношения от значения относительного уровня входного сигнала, под которым понимается логарифмическая мера передачи вида р_с= =20lg(s_c/s_смакс), для различных значений коэффициента k.

При построении зависимости имелось в виду, что при s_с < s_смакс преобладают шумы квантования, а при s_с >s_смакс преобладают шумы ограничения. Полученные графики имеют явно выраженные максимумы отношения сигнал/шум, положение которых несколько смещено от точки, где s_с =s_смакс.

А_S=10lg W_c / W_S k₃ k₂ k₁ А_огр=10lg W_c / W_огр

A_кв = 10lgW_c / W_кв

k₃ < k₂

k₂ < k₁

А_тр

k₁

р_с

D

Рис.2. Защищенность от шумов квантования и ограничения в зависимости

от относительного уровня входного сигнала

Из рассмотрения графиков рис.2 следует, что при равномерном квантовании существует оптимальный уровень входного сигнала, при квантовании которого отношение сигнал/шум оказывается наибольшим. Отклонение уровня входного сигнала, как в сторону уменьшения, так и в сторону увеличения, приводит к снижению защищенности.

По полученным характеристикам можно определить диапазон (условно динамический) уровней входных сигналов D при известном коэффициенте k , в пределах которого защищенность окажется не ниже требуемых значений - А_тр . Значение D легко может быть определено графически, как показано на рис.2.

С другой стороны, задавшись минимально допустимым значением защищенности и диапазоном изменений уровней входных сигналов, можно определить необходимую разрядность (или длину) кодовой комбинации при кодировании отсчета АИМ на выходе квантующего устройства при равномерном квантовании. Рассмотрим этот вопрос для случая кодирования телефонных сигналов, поступающих от различных источников. Пусть требуется обеспечить защищенность от шумов квантования не менее А_кв= 25 дБ для всех абонентов. Из (28) следует, что для самых слабых сигналов заданная защищенность будет обеспечена при m=(42,2+25)/6 »12(округляется в сторону большего целого), что соответствует числу уровней квантования М=2¹²=4096. При этом защищенность для сигналов с максимальной амплитудой (сильных сигналов) будет более чем на 30 дБ превышать требуемую защищенность. Большое число разрядов кода при равномерном квантовании приводит к усложнению аппаратуры и увеличению пропускной способности трактов, что экономически невыгодно. Устранить указанный существенный недостаток можно, осуществляя неравномерное квантование.

Оценка шумов квантования при неравномерном квантовании. При неравномерном квантовании шаг квантования не остается постоянным, а является переменным и изменяется по определенному закону. Если потребовать постоянства защищенности от шумов квантования в заданном динамическом диапазоне для всех уровней входных сигналов, то можно легко определить, воспользовавшись формулами (8) и (10), зависимость шага квантования от мгновенного значения напряжения u_вх ( или тока) квантуемого сигнала:

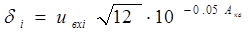. ( 36 )

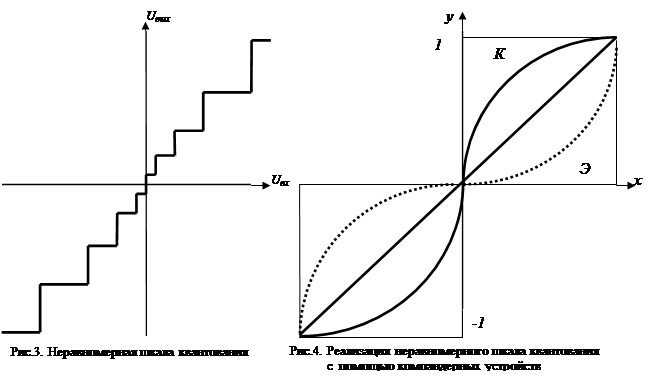
Из формулы (36) следует, что для слабых сигналов шаг квантования должен быть минимальным и возрастает с увеличением напряжения (тока) сигнала, т.е. должна быть нелинейная шкала квантования. Амплитудная характеристика соответствующего квантующего устройства при неравномерном квантовании показана на рис.3. Получение переменного шага квантования может быть реализовано следующими способами:

1) сжатием динамического диапазона с помощью компрессора ( К ) динамического диапазона сигнала перед кодированием его в кодирующем устройстве с линейной шкалой квантования и последующем его расширением экспандером ( Э ) после декодирования, рис.4; совокупность операций, проводимых компрессором и экспандером, называется компандированием сигнала; характеристика компандирования ( К-Э ), т.е. каскадного соединения компрессора и экспандера, должна быть линейной;

0

2)нелинейным кодированием и декодированием;

3) цифровым компандированием.

Указанные способы практически равноценны, но для теоретических исследований, последующих выводов и дальнейшей реализации различных методов неравномерного квантования, рассмотрим неравномерное квантование с помощью компандирования сигнала.

Для зависимости, изображенной на рис.4, где по осям отложены нормированные значения входных x=U_вх/U_вхмакс и выходных y=U_вых/U_{выхмакс} сигналов, добиваются того , чтобы при изменении Dх приращение Dy было бы постоянным, а приращение Dх -обратно пропорционально наклону характеристики, т.е.

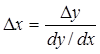. ( 37 )

Соответственно шаг квантования по оси х будет равен

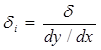. ( 38 )

Если число уровней квантования М в нормированном ( от 1 до минус 1) диапазоне, то

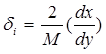. ( 39 )

Среднюю мощность шума, обусловленного неравномерным квантованием, можно определить по выражениям (5)...(8), если вместо шага квантования d_i подставить его значение в каждом шаге квантования. Подставив выражение (39) в формулу (7), получим

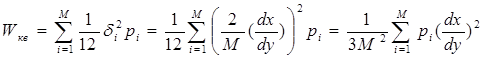( 40 )

Для расчета мощности шумов квантования при большом числе уровней квантования М операцию суммирования можно заменить интегрированием, тогда

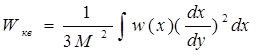, ( 41 )

здесь w(x) - плотность распределения вероятности нормированного сигнала на входе квантующего устройства.

Мощность сигнала можно выразить через его плотность распределения вероятности w(x) нормированного сигнала на выходе квантующего устройства

.

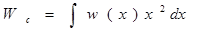Тогда отношение сигнал-шум квантования (ОСШК) с учетом (41) будет иметь вид

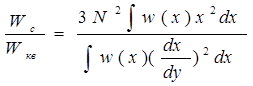. ( 42 )

Для обеспечения постоянства ОСШК необходимо, чтобы

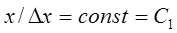. ( 43 )

Подставив в формулу (43) выражение (37), получим

.

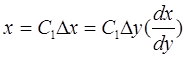Так как Dy постоянно, то получим

dy = C₂ ( dx/x ).

Проинтегрировав правую и левую части последнего выражения, получим

y = C₂ lnx + lnm ,

где lnm - постоянная интегрирования.

Отсюда

y = C₂ ln(mx). ( 44 )

Для нахождения постоянных этого выражения необходимо учитывать граничные условия закона изменений y = f(x): 1) при x=0, y=0 и 2) при x=1, y=1.

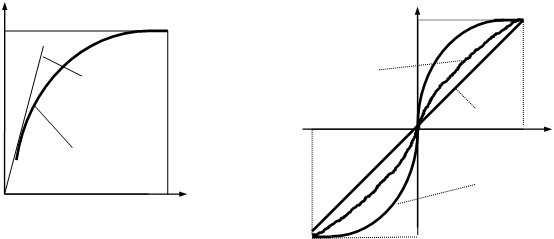
Первое условие приводит к нереализуемому результату. Зависимость полученной функции не переходит через начало координат (рис.5). Чтобы обеспечить реализацию, следует несколько изменить выражение (44) или изменить начальные условия.

y y

1 1

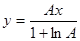m=25

m=0 1

x

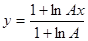m =100

-1

Рис.5. Логарифмический А- закон Рис.6. Характеристики m - закона

компандирования компандирования

При изменении выражения (44) под знак логарифма вводим постоянную С₃ :

С₃y = C₂ ln (mx + C₃ ), ( 55 )

тогда, подставляя нулевые граничные условия, получим значение постоянной С₃=1. Подставив второе граничное условие, найдем значение для С₂

С₂ = 1/ ln(m + 1).

Подставив последнее выражение в (55) и учитывая, что С₃=1, получим,

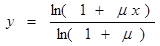. ( 56 )

Компандирование, осуществляемое по закону, описываемому формулой (56), называется логарифмическим с характеристикой типа m (или m - закон компандирования). Параметр m называется коэффициентом сжатия и определяется из соотношения

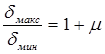( 57 )

здесь d_макс и d_мин - максимальное и минимальное значение шага квантования соответственно. Чем больше коэффициент сжатия m , тем больше разница между m_макс и m_мин. Вид характеристики m - закона компандирования для различных значений коэффициента сжатия m показан на рис. 6. Выбор коэффициента сжатия зависит от характеристик входных сигналов. В существующих цифровых системах передачи принимают m = 255.

Для больших значений коэффициента сжатия m защищенность от шумов квантования двуполярных сигналов может быть определена по формуле:

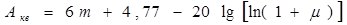. ( 58)

Из последнего выражения следует, что выбор коэффициента сжатия оказывает большое влияние на защищенность от шумов квантования.

Если m =250, то для m=7 имеем А_кв = 32 дБ, а при m=8 соответственно А=38 дБ.

Вернемся к выражению (44). При изменении начальных условий реализацию обеспечивают таким образом. Будем считать, что равенство (44) действительно только на участках от у=1 до точки х₁ ( см. рис. 5), в которой касательная к функции у(х) проходит через начало координат (штриховая линия), то на основании (44) и второго граничного условия получим:

C₂ = 1 / ln m

и, следовательно,

.

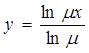Если теперь принять m=еА, где е - основание натуральных логарифмов, то

.

Так как эта функция действует только до определенной точки характеристики х₁, после которой логарифмическая характеристика переходит в касательную прямую, проходящую через начало координат, то

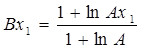. ( 59 )

В это точке равны производные обеих функций , т.е.

,

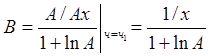или

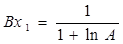. ( 60 )

Приравняем выражения (59) и (60):

1 + lnAx₁ = 1,

что возможно, если х₁ = 1/А. Отсюда В=А/(1+lnA).

Тогда

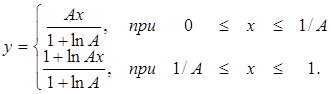( 61 )

Закон компандирования, описываемый выражениями (61), называется А-законом. Параметр А, называемый параметром сжатия (компрессии), обычно выбирается равным 87,6. Этот закон компандирования нашел широкое применение в Европейских странах, в том числе и России. Входные сигналы, напряжение которых меньше U_макс / А, подвергаются линейному кодированию, а сигналы, напряжение которых больше U_макс / А, подвергаются неравномерному квантованию по логарифмическому закону.

Нелинейное квантование позволяет значительно улучшить защищенность А_кв в области малых сигналов за счет ее некоторого снижения для сигналов с большим уровнем. Выигрыш от компандирования DА прямо пропорционален крутизне характеристики компрессии (сжатия) и для слабых сигналов может быть определен отношением шага квантования равномерного квантования к шагу квантования неравномерного квантования при U_вх® 0. Мощность шумов квантования при равномерном квантовании рассчитывается по формуле (8). При неравномерном квантовании для слабых сигналов она будет определяться наименьшим шагом квантования:

W_кв = d_мин / 12.

Тогда выигрыш в защищенности за счет неравномерного квантования

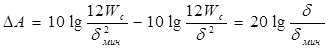, (62 )

здесь W_c - мощность полезного сигнала.

Шаг квантования зависит от крутизны характеристики компрессора (см. рис.4) и согласно выражению (38), отношение d/d_мин равно dy/dx. При компандированию по А-закону для сигналов меньших или равных значениям 1/А (выражение 61) производная dy/dx = A/(1+ln A) и для А=87,6 выигрыш в защищенности от шумов квантования будет равен DА=24 дБ.

Для сравнения на рис.7 приведены зависимости А_кв защищенности от входного уровня сигнала р_вх при равномерном (линейном), линия 1, и неравномерном (нелинейном квантовании), линия 2.

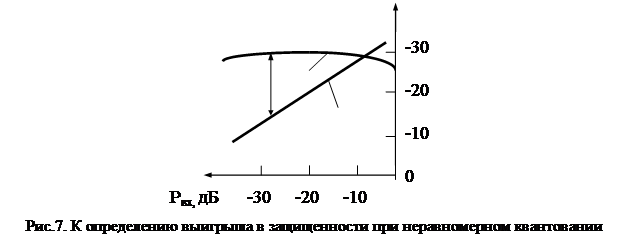А_кв, дБ

2

DА

1

Таким образом, неравномерное квантование для А-закона компандирования позволяет, увеличив защищенность на 24 дБ, уменьшить на 24/6=4 число разрядов кода, обеспечив требуемую защищенность от шумов квантования для наиболее слабых речевых сигналов при 8-разрядном кодировании вместо 12-разрядного при равномерном (линейном) квантовании.

В современных цифровых системах передачи используют цифровые компандерные устройства (компрессоры и экспандеры - сжиматели и расширители), которые объединены и взаимодействуют вместе с кодирующими и декодирующими устройствами. При этом в качестве функции у(х) применяют характеристику гипотетического компрессора, которая представляет собой аппроксимацию одного из законов компандирования (m или А) ломанной линией.

Энергетический спектр шума квантования.Шум квантования, образующийся в результате дискретизации и квантования, представляет собой последовательность некоррелированных импульсов со случайной амплитудой (рис.1б). Энергетический спектр такой последовательности описывается выражением

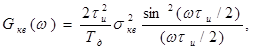( 63 )

где t_и - длительность импульса; Т_д - периоддискретизации; s_кв - дисперсия шума квантования. Форма энергетического спектра шума квантования показана на рис. 8.

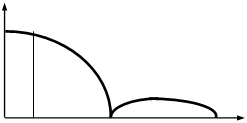G_кв(w)

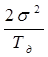
w

2p/Т 2p/t_и 4p/t_и

Рис. 8. Энергетический спектр шумов квантования

Из (63) следует, что по мере уменьшения длительности импульсов отсчетов t_и энергетический спектр шума квантования становится все более равномерным и при t_и® 0 шум квантования превращается в “белый шум”, имеющий постоянный энергетический спектр в широкой полосе частот, значительно превышающей ширину спектра сигнала.

Как отмечалось ранее (см. Лекция 9), демодуляция АИМ сигнала осуществляется фильтром нижних частот (ФНЧ) , частота среза которого равна верхней частоте спектра сигнала F_макс. Поскольку квантованный АИМ сигнал на входе демодулятора можно рассматривать как сумму исходного АИМ сигнала и шума квантования, для оценки отношения сигнал-шум квантования (ОСШК) на выходе демодулятора рассмотрим прохождение через ФНЧ неискаженного сигнала и шума.

Мощность низкочастотной составляющей спектра АИМ сигнала в Т_д /t_и раз меньше мощности исходного сигнала ( для m_а= 1), а максимальная частота этого спектра не может превышать половины частоты дискретизации. Мощность шума квантования на выходе демодулятора АИМ сигнала в полосе частот от нуля до половины частоты дискретизации W_д / 2 будет равна

.

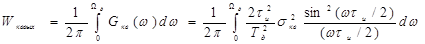На верхней частоте W_д / 2 аргумент wt_и / 2 = .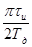

При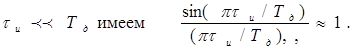

Тогда выражение для мощности шумов квантования принимает вид

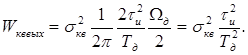( 64 )

Дата добавления: 2014-08-04; просмотров: 2349; Нарушение авторских прав

Мы поможем в написании ваших работ!