Корреляционно - регрессионный метод анализа

Корреляционный анализ используется для выявления стохастической взаимосвязи между показателями. Различают парную и множественную корреляцию.

Парная корреляция - это связь между двумя показателями, один из которых является факторным, а другой - результативным.

Множественная корреляция - влияние нескольких факторов на результативный показатель.

Аналитически связь между показателями описывается уравнениями, которые обосновываются с помощью графиков, аналитических группировок: уравнение прямой 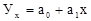; параболы 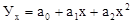; гиперболы 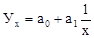и т.д.

Расчет уравнения связи 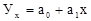сводится к определению параметров а₀и а₁методом наименьших квадратов, решением системы уравнений:

,

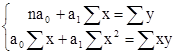где n - число единиц совокупности; х – величина факторного признака;

у – величина результативного признака.

Значения ∑х, ∑у, ∑х2, ∑ху рассчитывают на основании фактических исходных данных.

Коэффициент а₀ - постоянная величина результативного показателя, которая не связана с изменением данного фактора, параметр а₁ показывает среднее изменение результативного показателя с повышением или понижением величины факторного на единицу его собственного измерения.

Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (теоретические) значения результативного показателя ().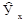

Для характеристики тесноты связи в случае прямолинейной зависимости используется коэффициент корреляции.

; ; .

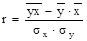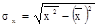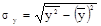Значения коэффициента корреляции могут находиться в пределах от -1 до +1, включая и ноль. Отрицательное значение коэффициент корреляции принимает тогда, когда между значениями х и у существует обратная зависимость. При отсутствии зависимости r_ух = 0. При r_ух = ±1 зависимость является прямолинейной функциональной. Т.е., чем ближе значение коэффициента корреляции к 1, тем сильнее взаимосвязь между факторным и результативным признаком.

Если коэффициент корреляции возвести в квадрат, получим коэффициент детерминации, показывающий, на сколько процентов зависит изменение результативного показателя от изменения факторного.

Коэффициент эластичности.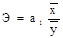

Он показывает, на сколько процентов в среднем изменится значение результативного признака при изменении факторного на 1%.

Дата добавления: 2014-02-26; просмотров: 319; Нарушение авторских прав

Мы поможем в написании ваших работ!