Методы случайного поиска в задачах оптимизации

Данные методы имеют ряд преимуществ перед градиентными регулярными методами:

1) быстро сходятся при многомерности исследуемой функции;

2) быстро сходятся если функция имеет овражный тип;

3) быстро сходятся к e-окрестности искомой точки.

Метод слепого поиска. Алгоритм метода можно записать в виде:

xⁱ⁺¹=xⁱ+ha, a – вектор направлений.

Производим генерацию точек до тех пор, пока f(xⁱ⁺¹)>f(xⁱ). Потом выбираем шаг и двигаемся ближе к искомой точке. Дойдя до окрестности точки метод будет производить пересчёт. Для остановки процесса можно либо уменьшить в два раза шаг, либо использовать градиентные и детерминированные методы.

Метод случайных направлений. Определяются случайные направления, накапливается статистика изменения функции, вычисляется статистический градиент и в направлении градиента делается пересчёт по формуле

xⁱ⁺¹=xⁱ+ha,

где 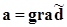(f(x_i).

Метод наказания случайностью. На первом этапе также выбирается случайная точка, генерируются случайные числа, и определяется статистический градиент и дальше по тому направлению детерминированными шагами делается пересчёт до тех пор, пока идёт изменение градиента.

Метод с блуждающим поиском.

Xⁱ⁺¹=xⁱ-hgrad(f(x))-h₁a.

Метод объединяет детерминированный подход, связанный с вычислением градиента функции и выбором шага h и метод случайного поиска, связанный с выбором случайного градиента и шага h₁.

Метод работает по следующему принципу. Определяется случайный градиент и делается пересчёт по алгоритму до тех пор, пока не будет произведено Ns холостых ходов, или пока не сойдется по точности e_зад<e_ост.

.

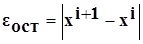
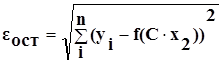Если отыскивается min, то производная должна быть отрицательной, а если max – положительной.

Метод случайного поиска для вычисления интегралов. Если определённый интеграл не имеет первообразной в аналитическом виде или процесс вычисления первообразной достаточно трудоёмок, то используют метод Монте-Карло, основанный на генерации и своеобразном подсчете случайных чисел.

Пусть требуется найти интеграл

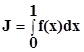
от функции y=f(x) методом Монте-Карло. Сначала генерируются случайные числа z, y_s, затем вычисляются y=f(z) (y_s – случайное число). Значения y и y_s сравниваются между собой. Если y_s(z)>y(z), то точка попала выше графика. В результате подсчитывается число точек выше графика и число точек ниже графика:

N_в= N_в+1, аналогично N_н= N_н+1.

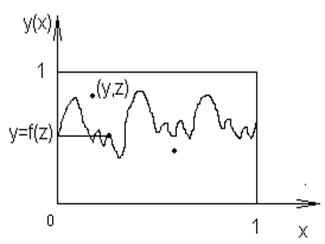
Рис.6.7. График функции

Площадь под графиком будет величиной определённого интеграла. Вычислим общее количество точек N= N_в+N_н. Доказывается, что при генерации достаточно большого числа случайных чисел определенный интеграл будет вычисляться по следующей формуле:

,

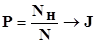где P – вероятность благоприятных событий (точек под графиком).

Вероятность и будет определять величину определённого интеграла.

6.7 Вопросы для самоконтроля

1. Что составляет основу численного метода?

2.Что можно описать рекурсивной программой?

3. Что представляет собой метод золотого сечения?

4. Опишите алгоритм метода золотого сечения.

5.Как согласно правилу знаков Декарта определить действительные корни?

6.В чем отличие метода случайности от метода наказания случайностью?

7.На чем основан метод Монте-Карло?

8.Для чего необходим градиент целевой функции?

Дата добавления: 2014-08-04; просмотров: 849; Нарушение авторских прав

Мы поможем в написании ваших работ!