Количественные характеристики надёжности

Предварительно рассмотрим понятие “случайная величина”.

Случайная величина - величина, которая в результате опыта можетпринять то или иное значение, причем заранее неизвестно, какое именно.

Примеры случайной величины:

1) Интервал времени между соседними отказами ЭВМ;

2) Интервал времени от начала работы изделия до первого отказа иливремя безотказной работы;

3) Число деталей, изготовленных рабочим в единицу времени.

Обозначим через T - время безотказной работы изделия (интервалвремени от начала работы изделия до первого отказа). Т – случайнаявеличина. Величина Т также называется наработка на отказ изделия, t -возможные значения случайной величины Т.

Введём понятие “вероятность безотказной работы”.

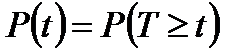- вероятность того, что время безотказной работы изделиябудет больше или равно некоторому значению t. Другими словами,вероятностью безотказной работы называется вероятность того, что призаданных условиях эксплуатации в течении интервала времени tневозникнет отказа, т.е.система будет работоспособна.

Вероятность отказа:

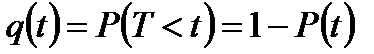
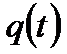- вероятность того, что время безотказной работы изделия меньшенекоторого заданного значения t.

Другими словами, вероятностью отказа является вероятность того, чтов течении заданного времени произойдёт хотя бы один отказ.

Функция 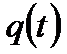представляет собой функцию распределения случайнойвеличины Т.

События В и С несовместные события (в опыте не могут появитьсявместе).

; ;

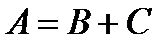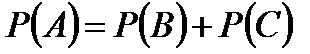откуда ; ; ;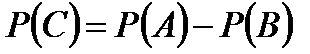

;

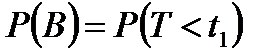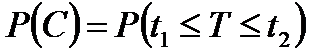Следовательно ;

или ;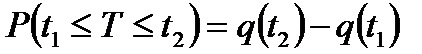

Введём в рассмотрение событиеA. Событие A означает, что T<t, т.е. винтервале времени от 0 до t отказа не произойдёт.

Введём в рассмотрение событие . Событие 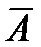означает, что Т<t, т.е. в интервале времени от 0 до t произойдёт отказ. События А и 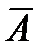являютсяпротивоположными, т.к. они образуют полную группу событий. Событияобразуют полную группу, если в результате опыта одно из них обязательнодолжно произойти.

Из теории вероятностей известно, что сумма вероятностейпротивоположных событий равна единице, т.е.

;

; ;

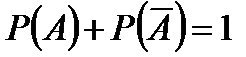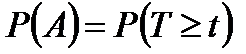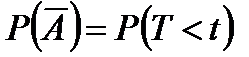Следовательно или

P(t) + q(t)=l

Для вероятности безотказной работы справедливо приближённое соотношение

, где

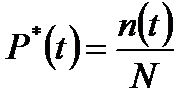
Здесь n(t) - число изделий, не отказавших к моменту времени t;

N - Число изделий, поставленных на испытания.

Испытания изделий должны проводиться при одинаковых условияхтак, чтобы отказы изделий были независимы друг от друга.

Для вероятности отказа справедливо приближённое равенство

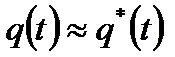; где .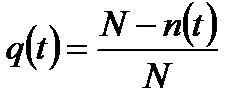

Здесь N - n(t) - число изделий, отказавших к моменту времени t.

1.8 Плотность вероятности f(t) времени безотказной работы Т

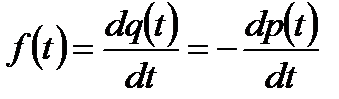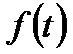; - частота отказов.

Здесь 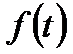- плотность вероятности случайной величины Т или частота отказов.

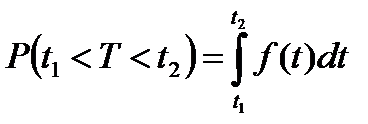→ вероятность того, что отказ изделия произойдёт

на интервале времени .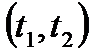

Для плотности вероятности времени безотказной работы Тсправедливо приближённое равенство:

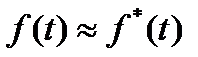, где 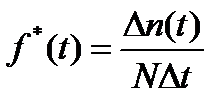- оценкачастотыотказов.

Здесь N - число изделий, поставленных на испытания, 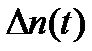- числоотказавших изделий на участке времени (t, t + ∆t).

1.9 Интенсивность отказов λ(t)

Рассмотрим вероятность безотказной работы изделия на промежуткевремени от t до t₁ при условии, что изделие до момента времени t неотказывало.

Обозначим эту вероятность через .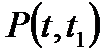

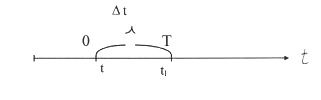
Событие А - изделие работало безотказно на интервале, времени от 0 до t.

Событие В - изделие работало безотказно на интервале времени от tдо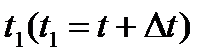

АВ - произведение событий А и В. Произведением событий А и Вявляется событие, заключающееся в совместном появлении этих событий.

Р(АВ) = Р(А) Р(В/А).

Р(В/А) - условная вероятность события В при условии, что событие Апроизошло (имело место).

Р(А) = P(t) - вероятность безотказной работы изделия на интервалевремени от 0 до t

Р(В/А) = Р(АВ) / Р(А); Р(В/А) =P .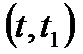

Но вероятность Р(АВ) есть вероятность безотказной работы изделия наинтервале

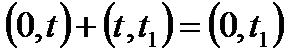; т.е. .

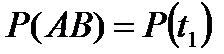Поэтому

.

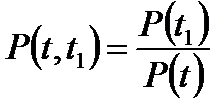Вероятность отката изделия на интервале 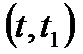равна

;

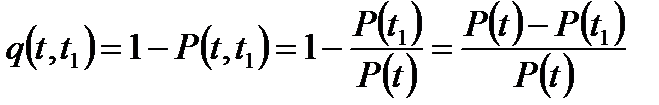Так как 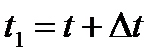, то

;

;

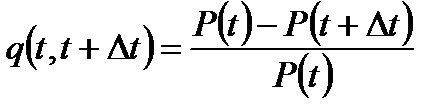
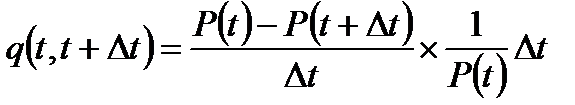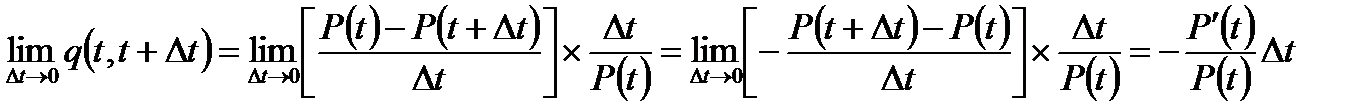Введём обозначение

;

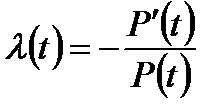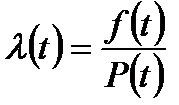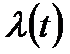; - интенсивность отказов.

Прималом ∆tимеем

.

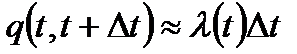Отсюда .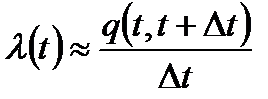

Из (1.3) видно, что интенсивность отказов представляет собойотношение вероятности отказа на интервале (t, t + At) к длине этогоинтервала (при малом ∆t).

Из (1.1) имеем

.

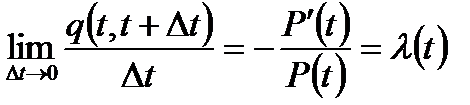Из (1.2) имеем

.

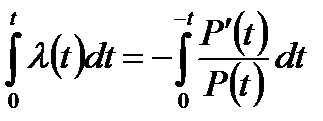Отсюда ;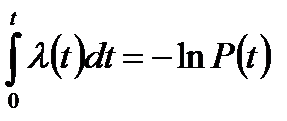

или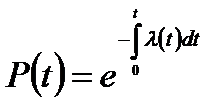

; ;

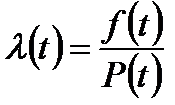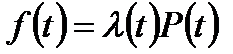или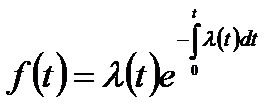

Для практически важного частного случая 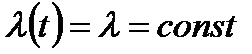; формула принимает вид

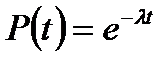
Формула называется экспоненциальным законом надёжности. На практике этот закон ввиду его простоты нашёл широкое применение при расчёте надёжности изделий.

График функции λ(t):

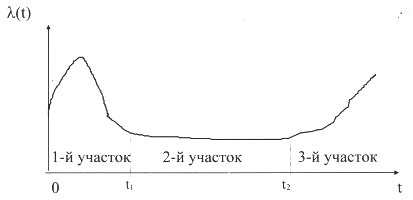
1 - й участок - период приработки изделия.

2-й участок - период нормальной работы.

3-й участок - период старения или износа изделия.

Дата добавления: 2014-08-09; просмотров: 430; Нарушение авторских прав

Мы поможем в написании ваших работ!