Применение уравнения Шредингера для анализа состояний квантовых систем

10.1. Микрочастица в одномерной "потенциальной яме"

Примером движения электрона в "потенциальной яме" является движение свободных (коллективизированных) электронов внутри металла. В классической электродинамике (см. "Основы электродинамики". Лекция 8) считалось, что вне металла потенциальная энергия электрона равна нулю, а внутри – отрицательна и численно равна работе выхода ( 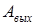). Иными словами, движение электронов ограничено потенциальным барьером прямоугольной формы с плоским дном.

Дано: микрочастица (электрон) находится в "потенциальной яме" глубиной - 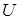и шириной - , т. е. в силовом поле :

при 0 < < ,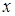

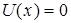при 0 < 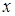и > .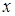

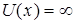Найти: вид волновой функции и собственные значения энер –

гии.

Поскольку силовое поле не за –

висит от времени, применим амплитудное уравнение Шредингера

,

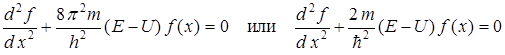тогда в интервале 0 < 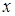< , т. е. в "потенциальной яме" функция 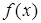, являющаяся решением данного уравнения 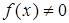, а вне ямы: .

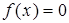Используем граничные условия. Поскольку функция 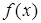должна удовлетворять условию непрерывности, т. е. микрочастица не может находиться вне ямы (в этом случае вероятность равна нулю), то

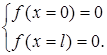В области 0 < x < , т. е. в яме: 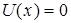и амплитудное уравнение имеет вид

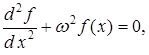где обозначено .

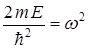Решением данного дифференциального уравнения будут функци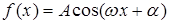и: или .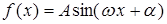

Удобнее выбрать и использовать второй вид решения (через sin), тогда из граничных условий:

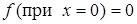следует, что .

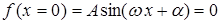Здесь 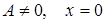, т. е. 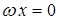, но 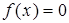. Это возможно, если a = 0.

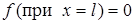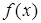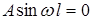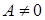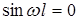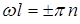Из аналогично . Так как функция непрерывна, то a = 0 и , причем , тогда и , где 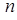= 1,2 3,4… - главное квантовое число. Отметим, что при 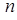= 0 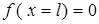, что физически невозможно, так как микрочастица нигде не находится (вероятность равна нулю).

Сравнивая полученные результаты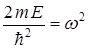

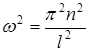или .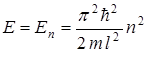

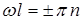
Данное соотношение - это совокупность собственных значений энергии, при которых решения амплитудного уравнения Шредингера будут иметь физический смысл.

Анализ:

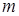1) Микрочастица (электрон) в "потенциальной яме" обладает дискретными значениями энергии, зависящими от величины главного квантового числа ( ), массы частицы ( ) и размера "ямы" – ( ). Здесь 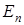- собственные значения энергии.

2) Значение 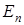- при = 1 - называется основным, остальные - возбужденными. Так как = 1, 2, 3, 4, … , то 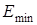для микрочастицы в потенциальной яме не равна нулю. Это же следует из волновой природы микрочастицы и соотношения неопределенностей:

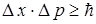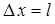. При и 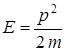с учетом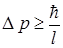

.

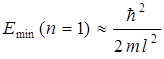Данное выражение с точностью до p² совпадает с полученным (см. выше).

3) Из решения дифференциального уравнения следует схема энергетических уровней электрона в "потенциальной яме" (см. рисунок) .

4) Вычислим "расстояние" между соседни-

ми уровнями, т. е. 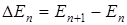. Тогда

.

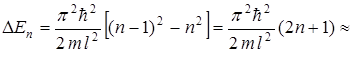
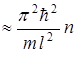Частные случаи:

а) Если 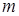= 10^-26 кг и » 10^-1 м ( модель молекул идеального газа ), то расчет дает 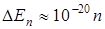[эВ]. Из этого следует, что энергетические уровни молекулы (атома) идеального газа расположены "густо", квантование энергии атома существует, но не сказывается и спектр энергий воспринимается как сплошной.

б) Если 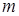= 10^-30 кг » 10^-1 м (модель "свободных электронов"), то 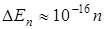[эВ], т. е. существенной разницы с предыдущим примером нет.

в) Если 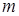= 10^-30 кг » 10^-10 м ( 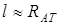- модель Томпсона), то 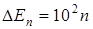[эВ] – дискретность уровней энергии электрона в атоме становится заметной.

5) Найдем вид функции 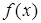. Так как 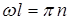, где - главное квантовое число, то 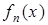- собственная функция и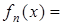

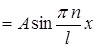. Используем условие нормировки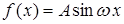

.

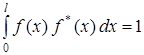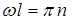
После подстановки

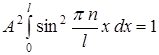или .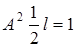

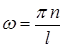
Отсюда 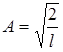, тогда

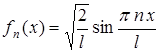, где = 1, 2, 3, 4 . . .

Вероятность нахождения мик- рочастицы на различных уча -

стках потенциальной ямы по определению

.

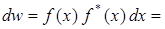
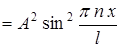Графики функци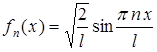й

и

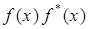приведены на ри-

сунках. Из полученных результатов следует, что у микрочастицы нет определенной траектории движения и все ее положения в "потенциальной яме" могут повторяться с определенной степенью вероятности. Например, при = 2 микрочастица не может быть в центре и на краях ямы, где ее вероятность равна нулю, но равновероятно ее нахождение как в левой, так и в правой частях "ямы".

6) Пусть "потенциальная яма" - трехмерная, тогда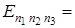

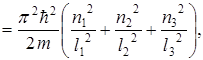где 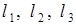- размеры "ямы" вдоль соответствующих осей координат ( 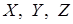). В этом случае собственным значениям энергии 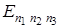соответствуют собственные функции 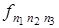, каждая из которых

.

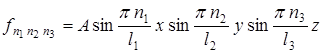Если "яма" кубическая, то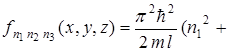

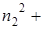
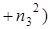и каждое значение 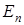может быть получено комбинацией целых чисел, например, пусть 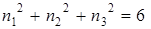, тогда

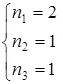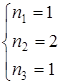или или ,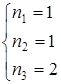

причем каждой тройке чисел соответствует своя функция 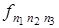, т. е. одному значению 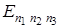( = 6), могут быть приписаны три состояния микрочастицы с волновыми функциями 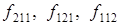. Такие состояния называются "вырожденными". Для данного примера кратность "вырождения" равна 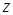= 3.

7) Чем больше значение главного квантового числа ( ), тем ближе квантовые представления к классическим.

8) С помощью волновой функции, как было показано выше, можно предсказать с какой вероятностью микрочастица может быть обнаружена в различных точках "потенциальной ямы". Наличие вероятностного подхода делает возможным "проникновение" (тунелирование) микрочастицы под потенциальным барьером конечной толщины. Это явление называется туннельным эффектом.

10.2. Квантовый гармонический осциллятор

В дальнейшем при рассмотрении конкретных задач мы не будем, как в предыдущем случае, полностью решать соответствующее дифференциальное уравнение. Его мы составим и дадим решение с последующим анализом.

В классической механике, на примере пружинного маятника (см. "Механика . . . ". Лекция 6) было получено дифференциальное уравнение классического гармонического осциллятора, колеблющегося под действием упругой 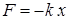или "квазиупругой" силы.

Пусть имеем квантовый линейный осциллятор, например, как в модели Томпсона: положительное ядро с зарядом 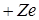(неподвижное) и колеблющийся около него электрон с зарядом 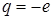. Тогда, как и в классическом случае, 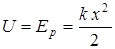, а электрон колеблется (как возле положения равновесия) с собственной частотой .

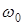Величина 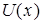не зависит от времени, тогда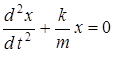

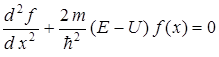или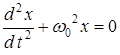

.

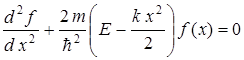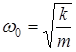
Решением данного уравнения будут собственные функции 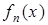и соответствующие им значения 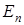, которые в данном случае имеют вид

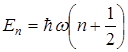, где = 0, 1, 2, 3, 4, . . . (главное квантовое число).

Анализ:

1) При = 0 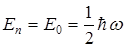- это минимальная энергия квантового осциллятора, которая называется нулевой энергией.

2) Собственные значения энергии квантового осциллятора квантованы и схема энергетических уровней приведена на рисунке. Шаг квантования равен 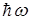, причем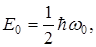

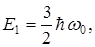
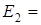
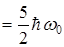и т. д.

3) Существование 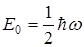при 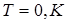доказано экспериментально при изучении рассеяния света в данных условиях. С позиций классической механики при 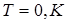движения нет и 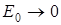. В квантовом осцилляторе при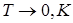 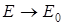, т. е. движение атомов в кристаллической решетке не прекращается.

4) Для квантового гармонического осциллятора переходы электрона (системы) из одного состояния в другое возможны только между соседними уровнями, т. е. D = = ±1. Это - "правило отбора".

5) Полная энергия квантового осциллятора определена, т. 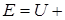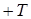е. , где 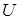- потенциальная, 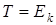- кинетическая энергии, но из соотношения неопределенностей следует, что вели -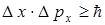

чины 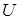и 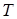- не определены. ( " Принцип допол - ~

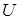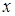
нительности "). ~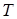

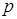
6) Становится понятным предположение Планка для излучательной способности абсолютно черного тела (см. Лекция 6). Энергия излучения должна быть кратной 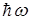, т. е. 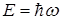. Однако, кроме данного, из полученного выражения следует и другой вывод о существовании .

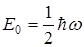10.3. Атом водорода

С позиций классической электродинамики между положительным ядром ( 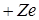) и электроном ( 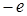) в атоме водорода Z = 1 потенциальная энергия взаимодействия определяется выражением 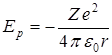(см. рисунок).

Здесь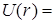

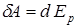
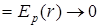
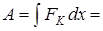
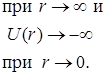
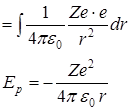
С позиций квантовой механики в данном случае электрон находит -

ся в объемной "потенциальной яме" без дна, т. е. яма не прямо -

угольной формы, а стационарное уравнение Шредингера имеет вид

.

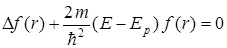Анализ:

1) Центрально – симметричный характер силового поля, в котором движется электрон, требует использования сферических координат при решении данного уравнения. (Решение можно найти в специальной литературе).

2) В квантовой механике данное уравнение решено и имеет однозначные, конечные и непрерывные решения при двух собственных значениях энергии. Первое - 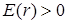, что физически означает: электрон "пролетает" вблизи ядра. Второе - 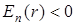, т. е. электрон "связан" с ядром в атом, причем его движение должно быть периодическим, а значения величины 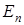квантованными.

3) Собственные значения энергии 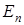(для второго случая), определяющие энергетические уровни электрона в водородоподобной системе имеют вид 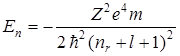, где 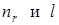, соответственно, радиальное и орбитальное квантовые числа. Схема энергетических уровней приведена на рисунке.

4) Если обозначить n_r + l + 1 = n, где n - главное квантовое число, то 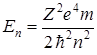, что совпадает с собственными значениями энергии атома водорода в модели Бора (см. Лекция 8). Таким образом, как и в классической механике, значения E_n, квантованы, а, следовательно, спектр излучения атома водорода – линейчатый.

5) Квантовое число 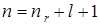совпадает с главным квантовым числом в теории Бора. Из данной формулы следует, что при данном величина орбитального квантового числа максимальна ( 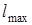), если 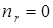, т. е. 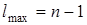. Следовательно, орбитальное квантовое число может принимать следующие значения

l = 0, 1, 2, 3 . . . (n - 1).

6) Решением уравнения Шредингера для водородоподобных систем являются собственные функции, содержащие три квантовых числа, т. е. . 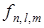, где - главное, - орбитальное, 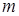- магнитное, причем на них накладываются ограничения:

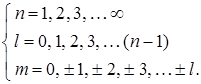
Еще раз отметим, что квантовые числа возникают при решении уравнения Шредингера.

10.4. Квантовые числа

Квантовыми числами называются целые или полуцелые числа, определяющие возможные дискретные значения физических величин систем, подчиняющихся законам квантовой механики.

Главное квантовое число ( ) - определяет энергетические уровни электрона (собственные значения энергии 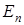электрона на данном энергетическом уровне). Может принимать значения = 1, 2, 3, 4 . . . . ¥.

В модели атома число n определяет энергетические слои.

Число 1 2 3 4 5 . . . .

Название слоя . . . .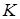

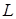
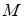
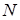
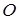Орбитальное квантовое число ( ) - определяет величину орбитального момента импульса (момента количества движения) электрона или форму орбиты. Может принимать

значения = 0, 1, 2, 3, . . . . ( - 1). Всего - значений. В модели Бора 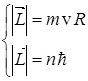, т. е. момент им - пульса квантован.

В квантовой механике при решении уравнения Шредингера получается, что момент импульса электрона тоже квантуется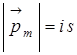

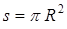
по формул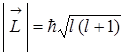е , где - орбиталь-

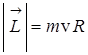
ное квантовое число.

Состояние электрона, обладающего различными значениями орбитального квантового числа, в атомной физике принято обозначать и называть:

0 1 2 3 4 5 6

cостояния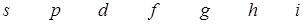

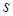– состояние электрона в атоме водорода при = 1 называется "основным". Орбитальное квантовое число определяет и форму орбиты:

Пусть = 4, тогда = 0, 1, 2, 3, т. е. любому квантовому числу отвечает -орбит раз -

ной формы: одна круговая и ( - 1) - эллиптических с раз -

ным эксцентриситетом. При 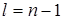- круговая орбита, при = 0 – эллипс с наибольшим эксцентриситетом.

Магнитное квантовое число ( 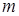) - характеризует ориентацию плоскости электронной орбиты в пространстве.

В классической физике предполагается, что движущийся по орбите электрон, эквивалентен круговому току, а вектора 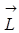и 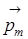- ориентированы относительно избранного направления внешнего магнитного поля (теория Ланжевена). Ориентация орбиты в этом случае задается углом d, причем .

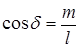Квантовая механика дает более точное выражение для такого способа ориентации орбиты, т. е.

.

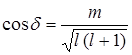В квантовой механике доказано, опытами О. Штерна и В. Герлаха, что существует так называемое пространственное квантование. Если рассматривать орбитальное квантовое число как вектор, характеризующий направление орбитального момента импульса 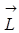, то возможно только такие ориентации орбиты в пространстве относительно произвольно выбранного направления внешнего магнитного поля, которым отвечают целочисленные значения числа 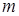, т. е. проекция 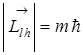, где 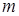- магнитное квантовое число. Может принимать значения 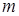= 0, ±1, ±2, . . . , ± , всего 2 + 1 – значений, т. е.

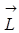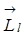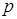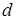-может принимать 2 +1 – ориентаций в пространстве. На рисунках приведены воз- можные ориентации век-торов для электронов в - и - состояниях. Прос -

транственное квантование

приводит к "расщеплению" энергетического уровня с заданным числом на 2 + + 1 – подуровней.

Таким образом, состояние электрона в атоме водорода определяется тремя квантовыми числами – главным , характеризующим значения 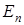, орбитальным , определяющим орбитальный момент количества движения электрона и магнитным 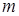, характеризующим ориентацию орбиты относительно выбранного направления. Это состояние описывается собственными волновыми функциями 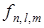, являющимися решениями уравнения Шредингера. Поскольку одному значению 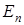соответствует не одно, а несколько состояний, различающихся квантовыми числами и 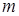, то такие состояния называются "вырожденными" (см. раздел 10.1), а кратность вырождения .

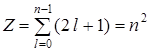Спиновое квантовое число ( 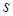) – характеризует собственный механический момент импульса 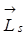электрона.

Собственный механический ( 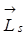) и собственный магнитный ( 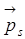) моменты электрона обнаружены в опытах Эйнштейна, де – Хааса, Барнеттом при изучении магнитоупругих явлений (см. "Основы электродинамики". Лекция 13).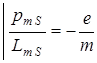

Спин электрона и других элементарных частиц следует рассматривать как особое свойство этих частиц, не имеющее аналогов в классической механике. Из общих выводов квантовой механики следует, что собственный механический момент импульса электрона должен быть квантован (как и орбитальный) по закону: 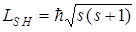, где 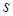- спиновое квантовое число.

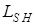Проекция спина на произвольно выбранное направление внешнего магнитного поля должна иметь 2 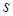+ 1 - ориентаций. Из опытов Штерна и Герлаха следует, что для электрона таких ориентаций существует всего две, т. е. 2 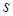+1 = 2 или 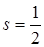(число одно, а направлений два).

Тогда как и для орбитального момента импульса электрона 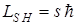или 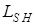= = 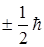. Спином обладают, как отмечено выше, и другие микрочастицы, причем -

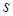может быть целым числом. Если 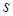= 0, 1, 2, . . . (в единицах 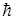), то такие частицы называются бозонами, например, p - и

k - мезоны, фотон, фонон, экситон. Части -

цы с 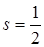, как и электрон, называются фермионами.

Итак, для полной характеристики состояния электрона в атоме необходимо знать 4 – квантовых числа. С учетом спинового квантового числа ( 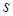) кратность "вырождения" в этом случае равна

,

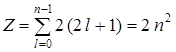где – главное квантовое число. Здесь ² – состояний (для электрона) со спином: 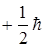, а другая половина ( ² - состояний) со спином: .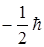

Отметим, что в модели атома кратность "вырождения" показывает максимальное число электронов, расположенных в атомном слое, соответствующем данному главному квантовому числу ( ).

Дата добавления: 2014-08-09; просмотров: 496; Нарушение авторских прав

Мы поможем в написании ваших работ!