
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Статистические оценки параметров распределения
Пусть распределение наблюдаемой случайной непрерывной величины 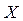 (признак генеральной совокупности), задается функцией плотности вероятности
(признак генеральной совокупности), задается функцией плотности вероятности 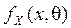 ,где
,где 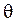 параметр или параметры распределения. Допустим, что вид функции
параметр или параметры распределения. Допустим, что вид функции 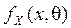 известен или ограничен некоторым классом функций, а параметр
известен или ограничен некоторым классом функций, а параметр 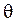 неизвестен и должен быть оценен по выборке
неизвестен и должен быть оценен по выборке 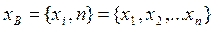 , где n – объем выборки.
, где n – объем выборки.
1. Точечные оценки
Точечной статистической оценкой параметров распределения или характеристик наблюдаемой случайной величины 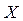 , называется построенная по данным выборки объема n величина:
, называется построенная по данным выборки объема n величина:
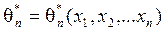 .
.
Оценка 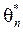 является так же случайной величиной, т.к. зависит от случайной выборки, поэтому ее можно представить как функцию от случайных величин
является так же случайной величиной, т.к. зависит от случайной выборки, поэтому ее можно представить как функцию от случайных величин 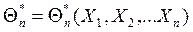 ,где
,где 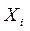 независимые случайные величины, распределенные так же как и сама величина
независимые случайные величины, распределенные так же как и сама величина 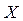 . Для того, чтобы оценки, получаемые по данным различных выборок соответствовали истинному значению параметра
. Для того, чтобы оценки, получаемые по данным различных выборок соответствовали истинному значению параметра 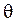 , оценка должна удовлетворять следующим требованиям.
, оценка должна удовлетворять следующим требованиям.
Оценка должна быть несмещенной, т.е. ее математическое ожидание должно совпадать с истинным значением параметра для любого объема n
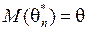
или хотя бы асимптотически несмещенной: 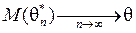 .
.
Оценка должна быть состоятельной, т.е. с ростом объема выборки оценка должна сходится по вероятности к истинному значению параметра:
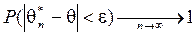 для любого
для любого 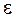
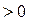 .
.
Для состоятельности оценки достаточно выполнения следующего:
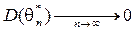 ,
,
действительно, из неравенства Чебышева 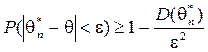
для случайной величины  следует состоятельность оценки.
следует состоятельность оценки.
Построенная оценка для использования на практике должна быть эффективной, т.е. ее дисперсия должна быть минимальной среди всех возможных оценок при фиксированном объеме выборки:
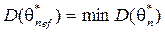 .
.
Величину дисперсии эффективной оценки можно найти используя неравенство Рао-Крамера:
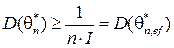 ,
,
где 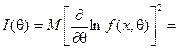
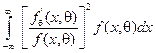 - информация Фишера. Коэффициент эффективности оценки
- информация Фишера. Коэффициент эффективности оценки 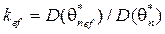 показывает степень эффективности оценки
показывает степень эффективности оценки  , если
, если 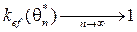 , то говорят об асимптотической эффективности оценки.
, то говорят об асимптотической эффективности оценки.
Отметим, что на практике не всегда удается удовлетворить всем перечисленным требованиям к оценке, но введенные свойства оценок всегда позволяют проранжировать имеющиеся оценки по их качеству.
В качестве примера рассмотрим оценки математического ожидания 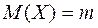 и дисперсии
и дисперсии 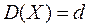 наблюдаемой случайной величины
наблюдаемой случайной величины 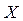 .
.
Построим точечные оценки:
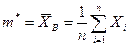 ,
, 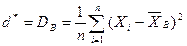
и рассмотрим их свойства. Поскольку 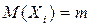 и
и 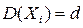 то можно вычислить, что для оценки m* справедливо:
то можно вычислить, что для оценки m* справедливо:
 ;
; 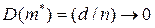 при
при 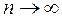 .
.
Из этого следует несмещенность и состоятельность оценки m*.
Рассматривая же оценку 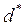 можно получить:
можно получить:
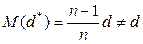 ;
; 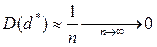 .
.
Из чего следует состоятельность, но и смещенность оценки 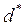 . Смещеность оценки здесь легко может быть исправлена. Рассмотрим оценку:
. Смещеность оценки здесь легко может быть исправлена. Рассмотрим оценку:
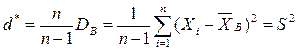 .
.
Видим, что оценка 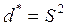 является уже не только состоятельной, но и несмещенной так как
является уже не только состоятельной, но и несмещенной так как 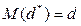 . Величина
. Величина 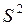 называется исправленной (уточненной) выборочной дисперсией, а величина
называется исправленной (уточненной) выборочной дисперсией, а величина 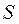 исправленным среднеквадратическим выборочным отклонением (выборочный стандарт).
исправленным среднеквадратическим выборочным отклонением (выборочный стандарт).
В заключении напомним, что относительная частота 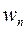 появления события в независимых испытаниях Бернулли является несмещенной, состоятельной и эффективной оценкой неизвестной вероятности этого события
появления события в независимых испытаниях Бернулли является несмещенной, состоятельной и эффективной оценкой неизвестной вероятности этого события  (теорема Бернулли), а эмпирическая функция выборочного распределения
(теорема Бернулли), а эмпирическая функция выборочного распределения 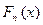 является состоятельной несмещенной оценкой неизвестной функцией распределения
является состоятельной несмещенной оценкой неизвестной функцией распределения 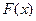 наблюдаемой случайной величины
наблюдаемой случайной величины 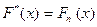 (теорема Гливенко).
(теорема Гливенко).
2. Методы построения точечных оценок
Метод моментов для нахождения точечных оценок неизвестных параметров распределения 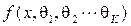 наблюдаемой в выборке случайной величины
наблюдаемой в выборке случайной величины 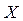 , состоит в приравнивании теоретических моментов к выборочным моментам. Для нахождения
, состоит в приравнивании теоретических моментов к выборочным моментам. Для нахождения 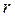 параметров
параметров 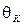 начальные
начальные 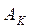 или центральные
или центральные 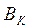 моменты до порядка
моменты до порядка 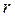 включительно приравниваются к соответствующим эмпирическим выборочным моментам
включительно приравниваются к соответствующим эмпирическим выборочным моментам 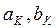 , тем самым получим систему
, тем самым получим систему 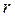 нелинейных уравнений метода моментов.
нелинейных уравнений метода моментов.
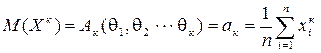 или
или 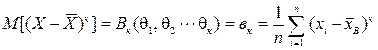 .
.
Например, построим оценку параметра, а случайной величины 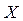 , имеющей треугольное распределение (рис.12.1), по заданной выборке
, имеющей треугольное распределение (рис.12.1), по заданной выборке 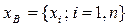 , где n – объем выборки:
, где n – объем выборки:
 f(x)
f(x)
+1




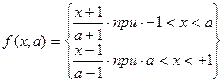

-1 0 a +1
Рис. 12.1. Треугольное распределение
Поскольку неизвестный параметр один то, вычисляя и приравнивая только первые начальные теоретические и эмпирические моменты
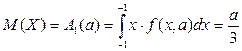 ,
, 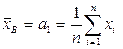 ,
,
получим оценку 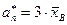 .
.
Метод моментов достаточно простой в применении и дает состоятельные оценки, однако их эффективность и несмещенность требуют дополнительных исследований.
Метод максимального правдоподобия основан на принципе правдоподобия, состоящем в том, что наблюдаемые в опыте события имеют большую вероятность, а маловероятные события практически не наблюдаемы. Вероятность наблюдения в опыте выборки 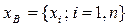 оценивается функцией правдоподобия
оценивается функцией правдоподобия
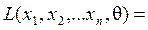
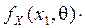
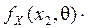 …
… 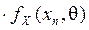 ,
,
поскольку данная нам выборка уже получена в опыте, то она должна обладать максимальным правдоподобием. За оценку 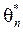 неизвестного параметра распределения
неизвестного параметра распределения 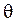 принимается его значение, при котором функция правдоподобия максимальна, поэтому уравнение метода для нахождения оценки
принимается его значение, при котором функция правдоподобия максимальна, поэтому уравнение метода для нахождения оценки 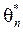 :
:
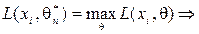
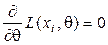 , при условии
, при условии 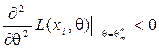 .
.
Для решения этих уравнений чаще используется логарифм функции правдоподобия 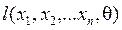
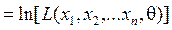 , поскольку максимум этих функций достигается при одном значении неизвестного параметра
, поскольку максимум этих функций достигается при одном значении неизвестного параметра 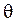 .
.
Например, рассмотрим случайную величину Пуассона 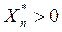 с плотностью распределения
с плотностью распределения 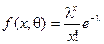 , где
, где 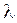 неизвестный параметр распределения. Тогда функция правдоподобия и уравнение метода имеют вид:
неизвестный параметр распределения. Тогда функция правдоподобия и уравнение метода имеют вид:
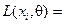
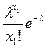
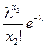 ….
…. 
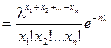
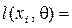
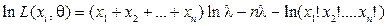
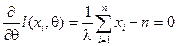

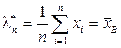 .
.
Доказано что метод максимального правдоподобия позволяет строить состоятельные и эффективные оценки.
Метод наименьших квадратов основан на идее минимизации суммы квадратов отклонения выборочных данных (или их функции) от строящейся оценки, он не требует знания закона распределения наблюдаемой случайной величины и кратко называется методом МНК.
Например, рассмотрим оценку дисперсии 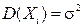 случайной величины по выборке
случайной величины по выборке 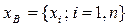 , где n – объем выборки. Построим функцию для квадратов отклонения
, где n – объем выборки. Построим функцию для квадратов отклонения 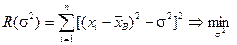 ,
,
из условия минимума 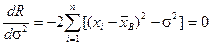 и
и 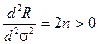 находим
находим
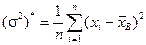 .
.
3. Интервальные оценки и алгоритм их построения
В отличие от точечных оценок типа 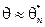 интервальные оценки задают интервал значений, где оцениваемый параметр находится с заданной вероятностью, т.е. это оценки типа
интервальные оценки задают интервал значений, где оцениваемый параметр находится с заданной вероятностью, т.е. это оценки типа 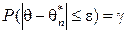 .
.
Надежностью оценки (доверительной вероятностью) называется вероятность 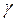 ,с которой оцениваемый параметр находится в интервале:
,с которой оцениваемый параметр находится в интервале:
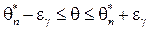 .
.
Полуширина доверительного интервала 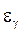 называется точностью оценки, соответствующей надежности
называется точностью оценки, соответствующей надежности 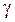 .Для построения доверительного интервала (нахождения по
.Для построения доверительного интервала (нахождения по 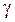 величины
величины 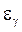 ) необходимо знать закон распределения оценки случайной величины
) необходимо знать закон распределения оценки случайной величины 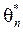 .
.
Пусть в выборке 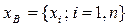 наблюдается нормальная случайная величина
наблюдается нормальная случайная величина 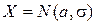 c неизвестными параметрами распределения а и
c неизвестными параметрами распределения а и 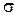 .
.
Построим доверительный интервал для математического ожидания а:
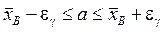 ,
,
принимая за точечную оценку а, величину 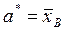 иучитывая что величина
иучитывая что величина 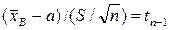 имеет распределение Стьюдента с
имеет распределение Стьюдента с 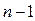 степенью свободы. Решение уравнения
степенью свободы. Решение уравнения 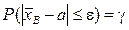 относительно
относительно 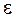 при заданном значении
при заданном значении 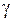 эквивалентно решению уравнения:
эквивалентно решению уравнения:
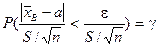 или
или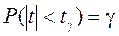 .
.
Его решение получим в виде 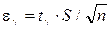 ,где
,где 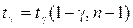 двухсторонняя квантиль Стьюдента (рис. 12.2).
двухсторонняя квантиль Стьюдента (рис. 12.2).
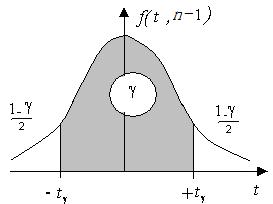
Рис. 12.2 Двухсторонняя квантиль Стьюдента
Построим теперь доверительный интервал для среднеквадратического отклонения 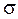 :
:
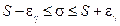 .
.
Принимая за оценку 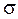 величину
величину 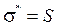 и учитывая, что величина
и учитывая, что величина 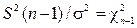 имеет
имеет 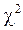 -распределение с n - 1 степенью свободы. Решение уравнение
-распределение с n - 1 степенью свободы. Решение уравнение 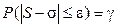 относительно
относительно 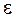 при заданном параметре
при заданном параметре 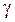 эквивалентно решению уравнения:
эквивалентно решению уравнения:
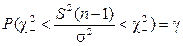 ,
,
тогда получим его решение в виде 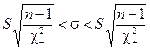 ,где величины
,где величины 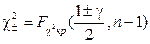 являются правосторонними “хи-квадрат” квантилями (рис.12.3).
являются правосторонними “хи-квадрат” квантилями (рис.12.3).
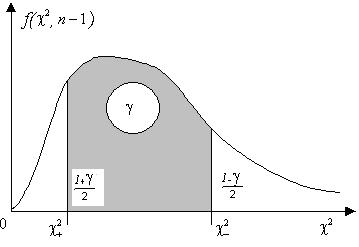
Рис. 12.3 Двухсторонняя “хи-квадрат”квантиль.
Пример: Пусть наблюдается выборка объемом n =16 со средним выборочным значением 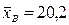 и выборочной дисперсией
и выборочной дисперсией 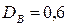 . Построить доверительные интервалы для неизвестного математического ожидания а и среднеквадратического отклонения
. Построить доверительные интервалы для неизвестного математического ожидания а и среднеквадратического отклонения 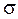 для надежности
для надежности 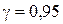 .
.
Исправленная дисперсия 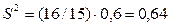 , а исправленное выборочное среднеквадратическое отклонение
, а исправленное выборочное среднеквадратическое отклонение 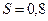 .
.
По таблице квантилей для распределения Стьюдента в приложении 3 находим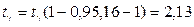 ,тогда
,тогда 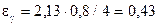 и тогда доверительный интервал для математического ожидания а будет таким:
и тогда доверительный интервал для математического ожидания а будет таким:
20,2-0,43< a<20,2+0,43 или 19,77< a<20,63.
По таблице для квантилей 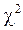 - распределения в приложении 4 находим
- распределения в приложении 4 находим 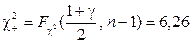
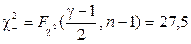 и тогда
и тогда 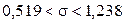 .
.
| <== предыдущая страница | | | следующая страница ==> |
| МАТЕМАТИЧЕЧСКАЯ СТАТИСТИКА | | | Применение уравнения Шредингера для анализа состояний квантовых систем |
Дата добавления: 2014-08-09; просмотров: 512; Нарушение авторских прав

Мы поможем в написании ваших работ!