
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Многоэлектронные атомы
Квантовая механика позволяет достаточно просто и, что самое главное, аналитически решить уравнение Шредингера для простейшего случая – атома водорода (Z = 1). Значительно сложнее обстоит дело для атомов, содержащих большое число электронов (Z > 1).
11.1. Принцип Паули. Классификация электронов
Потенциальная энергия многоэлектронного атома состоит из энергии взаимодействия электрона с ядром 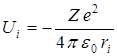 , где
, где 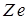 - заряд ядра, и энергии отталкивания от других электронов
- заряд ядра, и энергии отталкивания от других электронов 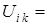
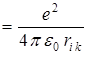 , где
, где  - расстояние между
- расстояние между 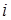 – м и
– м и 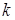 – м электронами, тогда уравнение Шредингера имеет вид
– м электронами, тогда уравнение Шредингера имеет вид
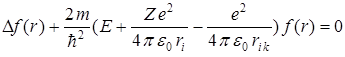 .
.
Наличие слагаемого Ui k не позволяет получить аналитического решения уравнения Шредингера, поэтому прибегают к приближенным методам. Один из таких методов, называемый методом "самосогласованного поля", предполагает, что электрон движется в некотором результирующем поле, образованном ядром и остальными ( 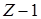 ) электронами (согласованное поле). При таком допущении движение электрона приближенно можно считать как движение в водородоподобном атоме, состоящем из ядра с зарядом -
) электронами (согласованное поле). При таком допущении движение электрона приближенно можно считать как движение в водородоподобном атоме, состоящем из ядра с зарядом - 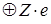 и сферически симметричной оболочки, образованной
и сферически симметричной оболочки, образованной 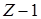 электронами, поэтому в описании свойств такого электрона сохраняется много общего с описанием свойств электрона в атоме водорода. В частности, состояние каждого электрона в атоме характеризуется теми же четырьмя (
электронами, поэтому в описании свойств такого электрона сохраняется много общего с описанием свойств электрона в атоме водорода. В частности, состояние каждого электрона в атоме характеризуется теми же четырьмя ( 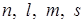 ) квантовыми числами. Наличие же взаимодействия между электронами в многоэлектронном атоме приводит к тому, что вырождение уровней энергии, характерное для атома водорода, у них снимается и каждому состоянию, характеризующемуся четырьмя квантовыми числами, соответствует свое (одно) значение энергии (
) квантовыми числами. Наличие же взаимодействия между электронами в многоэлектронном атоме приводит к тому, что вырождение уровней энергии, характерное для атома водорода, у них снимается и каждому состоянию, характеризующемуся четырьмя квантовыми числами, соответствует свое (одно) значение энергии ( 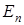 ).
).
Приближенное решение уравнения Шредингера методом "самосогласованного поля" позволяет определить энергетические уровни, на которых могут размещаться электроны. Если бы электроны были классическими частицами, то при 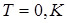 они все разместились бы на самом низком уровне, а все другие были бы пустыми. В действительности распределение электронов по их состояниям управляется принципом Паули, установленным на основе обобщения большого экспериментального материала. Существует несколько формулировок принципа Паули, поэтому мы остановимся на двух наиболее часто встречающихся:
они все разместились бы на самом низком уровне, а все другие были бы пустыми. В действительности распределение электронов по их состояниям управляется принципом Паули, установленным на основе обобщения большого экспериментального материала. Существует несколько формулировок принципа Паули, поэтому мы остановимся на двух наиболее часто встречающихся:
1. "В каждом состоянии, характеризующемся четырьмя квантовыми числами – 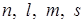 , может находиться только один электрон".
, может находиться только один электрон".
2. "На любом энергетическом уровне могут находиться только два электрона, причем с разными спинами".
Ниже приведена теоретическая периодическая таблица элементов, построенная из решения уравнения Шредингера для многоэлектронного атома и в соответствии с принципом Паули. Математически этот принцип записывается 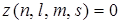 или = 1.
или = 1.
| Гл. квант. число (n) | ||||||||||||||||||||||||
| Символ слоя | K | L | M | N | ||||||||||||||||||||
| Максимальное число электронов в слое (z=2n2) | ||||||||||||||||||||||||
Число подоболочек 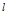 ,
где ,
где 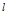 = = 0, 1,
2, . . . ,
(n-1) = = 0, 1,
2, . . . ,
(n-1)
| ||||||||||||||||||||||||
| Символ подоболочки (подгруппы) | 1s | 2s | 2p | 3s | 3p | 3d | 4s | 4p | 4d | 4f | ||||||||||||||
| Число электронов в подоболочке 2(2l+1) | 6(2/4) | 6(2/4) | 10(2/4/4) | 6(2/4) | 10(2/4/4) | 14(2/4/4/4) | ||||||||||||||||||
| Число подуровней (m) |
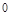
|
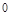
|
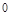
|
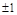
|
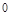
|
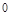
|
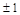
|
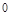
|
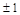
|
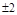
|
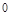
|
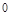
|
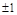
|
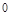
|
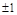
|
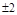
|
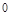
|
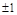
|
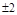
|
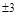
| ||||
| Спиновое число (s) | 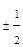
| 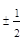
| 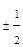
| 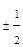
| 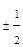
| 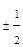
| 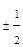
| 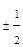
| 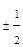
| 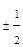
| 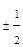
| 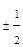
| 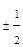
| 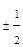
| 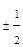
| 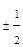
| 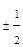
| 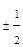
| 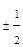
| 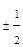
| ||||
Из таблицы следует:
1) Число электронов в каждом слое соответствует числу элементов в периоде. Элементы, у которых заполняется один и тот же электронный слой, объединены в периоды. Так, первый период должен содержать - 2 элемента, второй - 8, третий - 18, четвертый – 32, пятый – 50 и т. д..
2) Каждый период заканчивается элементом, у которого полностью укомплектован (заполнен) электронный слой. Электронная оболочка такого атома обладает сферической симметрией и очень устойчива, поэтому он не склонен отдавать или приобретать дополнительные электроны, т. е. в химическом отношении должен быть инертным.
3) Началом каждого периода служит элемент, у которого начинается комплектование (заполнение) нового электронного слоя, причем связь этих электронов с ядром будет относительно слабой, т. к. симметричные электронные облака укомплектованных внутренних оболочек атома предельно компенсируют заряд ядра. Поэтому в начале каждого периода должен стоять типичный металл. Сравним теоретическую таблицу с реальной (таблица элементов Д. И. Менделеева).
| Номер слоя (n) | Наименов. слоя | Число электронов в слое (кол-во элементов) | Обознач. уровня | Число эл-нов на уровне 2(2l + 1) | Число подуровней (m) |
| - 5 p - 4 d - 5 s | |||||
| N | - 4 p - 3 d - 4 s | ||||
| M | - 3 p - 3 s | ||||
| L | - 2 p - 2 s | ||||
| K | - 1 s |
E
Совпадения и отличия:
1) В первом слое (периоде) два элемента, причем второй – гелий – инертный газ (закончилось заполнение К - слоя).
2) Во втором слое - 8 элементов. Первый элемент - Li (началось формирование L -слоя), восьмой – Ne (заполнение L - слоя закончилось).
3) В третьем M - слое должно быть 18 элементов, а их только 8. Это обусловлено тем, что сферическая симметрия электронного облака достигается не только тогда, когда слой полностью укомплектован 8 электронами, но и значительно раньше: когда заполнены 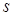 и
и 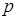 - оболочки, способные вместить 8 электронов.
- оболочки, способные вместить 8 электронов.
4) Различия в количестве электронов слоя наблюдается и далее (N, O, . . . - слои), т. е. энергетическое состояние уровней не соответствует порядку, свойственному свободному атому. Это связано с тем, что допущение: "Большим квантовым числам соответствуют большие значения энергии" - для сложных атомов не всегда выполняется. Так, 4 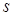 – состояние энергетически более низкое, чем 3
– состояние энергетически более низкое, чем 3 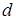 – состояние, аналогично 5
– состояние, аналогично 5 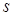 – и 4
– и 4 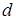 – состояния.
– состояния.
5) Энергия связи внешних электронов с ядром уменьшается с увеличением номера элемента, а свойства атома определяются состоянием именно верхних энергетических уровней.
6) Распределение электронов по состояниям записывается 1 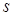 2 2
2 2 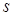 2 2
2 2 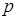 6 3
6 3 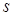 2 3
2 3 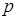 6 4
6 4 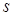 2 3
2 3 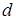 10 4
10 4 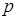 6 5
6 5 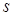 2 4
2 4 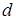 10 5
10 5 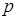 6 . . . , где 1, 2, 3, 4 . . . - номер слоя,
6 . . . , где 1, 2, 3, 4 . . . - номер слоя, 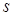 ,
, 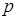 ,
, 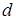 . . . - символ подоболочки, показатель степени - число электронов.
. . . - символ подоболочки, показатель степени - число электронов.
11.2. Энергия молекул
Экспериментально установлено, что силы, удерживающие атомы в молекуле, вызваны взаимодействием внешних электронов, а электроны внутренних оболочек при объединении атомов в молекулу остаются в прежних состояниях.
Различают два вида связи атомов: гемеополярная (ковалентная) и гетерополярная (ионная). Первая образуется обобществлением пары электронов от разных атомов, причем электроны имеют разные спины. Примером такой связи являются молекулы H2, N2, O2. Схема приведена ниже
В такой молекуле пара электронов расположена симметрично относительно ядер атомов. Если в молекулу объединяются разные атомы, то при ковалентной их связи, например, молекула 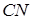 , электронные пары располагаются асимметрично, благодаря чему молекула приобретает электрический дипольный момент.
, электронные пары располагаются асимметрично, благодаря чему молекула приобретает электрический дипольный момент.
Другой вид связи – гетерополярная (ионная). Эта связь обусловлена тем, что у одного из ядер атомов образуется избыток, а у другого недостаток электронов. Таким образом, молекула как бы состоит из двух ионов противоположных знаков, притягивающихся друг к другу. Примером такой связи могут служить 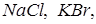
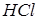 и др.
и др.
 Одной из простейших молекул с гемеополярной связью является молекула водорода: состоящая из двух протонов (ядра атома водорода) и двух электронов.
Одной из простейших молекул с гемеополярной связью является молекула водорода: состоящая из двух протонов (ядра атома водорода) и двух электронов.
В. Гайтлер и Ф. Лондон составили и решили уравнение Шредингера для данной модели.
Оказалось:
1) Собственные значения энергии 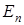 зави -
зави -
сят от расстояния ( 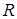 ) между ядрами.
) между ядрами.
 2) Значения
2) Значения 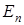 зависят от ориентации спинов:
зависят от ориентации спинов:
- "параллельной" и ¯ - "антипараллель -
ной".
3) Значения 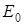 , к которому стремится энергия молекулы при
, к которому стремится энергия молекулы при 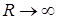 для обеих кривых одинаково и равно сумме энергий изолированных атомов.
для обеих кривых одинаково и равно сумме энергий изолированных атомов.
4) Существует 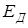 - энергия связи. Это та минимальная энергия, которую необходимо сообщить молекуле, чтобы "разорвать" ее на атомы.
- энергия связи. Это та минимальная энергия, которую необходимо сообщить молекуле, чтобы "разорвать" ее на атомы.
5) Изменение энергетического запаса энергии молекулы происходит за счет изменения ее составляющих, т. е. полная энергия 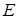 равна
равна
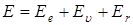 ,
,
где 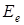 - энергия, связанная с электронной конфигурацией молекулы (электронная энергия),
- энергия, связанная с электронной конфигурацией молекулы (электронная энергия), 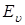 - энергия, соответствующая колебаниям молекулы (колебательная или вибрационная энергия),
- энергия, соответствующая колебаниям молекулы (колебательная или вибрационная энергия), 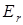 - энергия, связанная с вращением молекулы (вращательная или ротационная энергия). Все составляющие независимы друг от друга и квантованы.
- энергия, связанная с вращением молекулы (вращательная или ротационная энергия). Все составляющие независимы друг от друга и квантованы.
6) Наличие составляющих в полной энергии молекулы проявляется в ее спектре поглощения. Ранее (см. Лекция 5) отмечалось, что молекулярный спектр – полосатый, т. е. состоит из множества линий, объединенных в полосы. Для каждого газа такой спектр индивидуален и каждой полосе соответствует свое значение величин 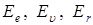 или их сочетаний.
или их сочетаний.
7) Существуют и спектры испускания молекул. Они возникают при обратном переходе из возбужденного состояния в стационарное, причем согласно правилу отбора "разрешены" лишь определенные переходы.
11.3. Возбуждение, спонтанное и вынужденное излучения
 Каждый химический элемент характеризуется индивидуальной, только ему присущей, схемой энергетических уровней. Для того, чтобы могло произойти излучение, электрону, находящемуся на разрешен -
Каждый химический элемент характеризуется индивидуальной, только ему присущей, схемой энергетических уровней. Для того, чтобы могло произойти излучение, электрону, находящемуся на разрешен -
ной орбите (основное состояние), а речь идет о внешних (валентных электронах), необходимо сообщить извне энергию (см. рис.). Это процесс возбуждения, который можно осуществить:
а) Нагревом вещества - при повышении температуры увеличивается число столкновений атомов и некоторые из электронов могут получить необходимую энергию.
б) Фотовозбуждение – электроны переходят на более высокие уровни за счет поглощения энергии падающих фотонов, как на рисунке. Это вынужденный (индуцированный) переход.
в) Электрическое возбуждение – при пропускании тока через газоразрядные лампы.
Продолжительность пребывания атома в возбужденном состоянии порядка 10-8 с.
Из возбужденного состояния электроны могут переходить на более низкий энергетический уровень. Схема энергетических уровней предполагает большое число таких переходов, однако, существует "правило отбора", ограничивающее их число. "В случае "разрешенных" переходов орбитальное ( 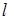 ) или спиновое (
) или спиновое ( 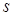 ) – квантовые числа меняются на единицу", т. е. математически это записывается в виде
) – квантовые числа меняются на единицу", т. е. математически это записывается в виде 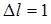 или
или 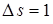 .
.
 При переходе (разрешен -
При переходе (разрешен -
ном) на более низкий энер -
гетический уровень элект -
рон испускает излучение в виде кванта 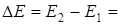
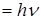 . Если такой переход
. Если такой переход
осуществляется без внешне-
го воздействия, то возни -
кающее излучение назы -
вается спонтанным. При на-
личии внешнего воздейст -
вия - излучение называется вынужденным. Вынужденное излучение вызывается внешним электромагнитным излучением и только соответствующей частоты.
 В силу "правила отбора" у атомов многих элементов имеются энергетические
В силу "правила отбора" у атомов многих элементов имеются энергетические
уровни, с которых электрон
не может "самостоятельно" перейти на более низкий уровень. Эти уровни назы-
ваются метастабильными состояниями ( 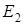 - см. рис.).
- см. рис.).
Перейти на такой уровень
электрон может при соуда -
рении с другим электроном или при каскадном переходе с более высокого уровня. Продолжительность пребывания атома в метастабильном состоянии составляет порядка 10-3 с .
При достаточно интенсивном возбуждении можно одновременно "перевести" на метастабильный уровень большую часть электронов, таким образом, происходит накопление энергии 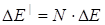 , где
, где 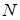 - число атомов. Энергия
- число атомов. Энергия 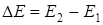 (см. схему) при дальнейшем переходе электронов в основное состояние испускается в виде интенсивного, монохроматического когерентного излучения (Принцип работы лазера).
(см. схему) при дальнейшем переходе электронов в основное состояние испускается в виде интенсивного, монохроматического когерентного излучения (Принцип работы лазера).
Излучение может возникать и в результате возбуждения атомов электронами высоких энергий, которые проникают внутрь атома и переводят близкие к ядру электроны ( 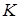 - слоя) на более высокие энергетические уровни. При обратном (последующем) переходе более удаленных от ядра электронов (
- слоя) на более высокие энергетические уровни. При обратном (последующем) переходе более удаленных от ядра электронов ( 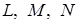 - слоев) на освободившийся энергетический уровень испускается излучение
- слоев) на освободившийся энергетический уровень испускается излучение
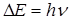 или
или 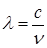 , длина волны которого лежит в рентгеновской области. Это излучение называется характеристическим.
, длина волны которого лежит в рентгеновской области. Это излучение называется характеристическим.
 Так как, электроны высоких энергий тормозятся, проникая в оболочку атома, т. е. теряют часть своей энергии, то эти потери проявляются в виде тормозного рентгеновского излучения с верхней границей nmax. Граничная энергия соответствует слу -
Так как, электроны высоких энергий тормозятся, проникая в оболочку атома, т. е. теряют часть своей энергии, то эти потери проявляются в виде тормозного рентгеновского излучения с верхней границей nmax. Граничная энергия соответствует слу - 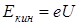 чаю, когда электрон излучает всю энергию
чаю, когда электрон излучает всю энергию 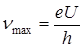 ,
, 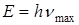 , где
, где 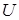 – разность потенциалов поля, в котором движется электрон.
– разность потенциалов поля, в котором движется электрон.
Для рентгеновского спектра излучения справедлив закон Мозли 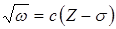 . "Частота спектральной линии (
. "Частота спектральной линии ( 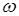 ) пропорциональна атомному номеру испускающего элемента (
) пропорциональна атомному номеру испускающего элемента ( 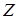 )". Здесь
)". Здесь 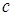 и s - константы, характерные для каждой линии спектра. Закон позволяет по измеренной длине волны (частоте) точно установить атомный номер элемента и сыграл большую роль при размещении атомных (химических) элементов в периодической системе.
и s - константы, характерные для каждой линии спектра. Закон позволяет по измеренной длине волны (частоте) точно установить атомный номер элемента и сыграл большую роль при размещении атомных (химических) элементов в периодической системе.
11.4. Квантовомеханическая модель атома (модель Шредингера)
Данная модель была разработана Шредингером на основе квантовой механики.
Согласно де – Бройлю, электрону, как и любой микрочастице с 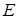 и
и 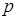 , отвечает волна с
, отвечает волна с 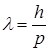 . Поскольку движущемуся вокруг ядра электрону отвечает стоячая волна, то длина электронной орбиты должна быть кратна целому числу таких волн, т. е.
. Поскольку движущемуся вокруг ядра электрону отвечает стоячая волна, то длина электронной орбиты должна быть кратна целому числу таких волн, т. е.
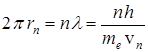 или
или 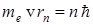
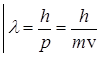
где 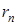 - радиус орбиты,
- радиус орбиты, 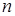 - главное квантовое число,
- главное квантовое число, 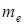 - масса электрона,
- масса электрона, 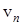 - скорость на
- скорость на 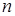 - орбите.
- орбите.
Анализ:
1) В квантовомеханической модели атома боровские орбиты заменены стоячими пространственными волнами. Каждой такой волне отвечают собственные значения энергии 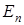 и частоты
и частоты 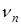 .
.
2) Полученное выражение совпадает с первым постулатом Бора (см. Лекция 8).
3) Вместо перехода с одной орбиты на другую в данной модели происходит переход из одного состояния, которому соответствует определенная стоячая волна, в другое (с другой волной).
4) Интенсивность волны в разных точках пространства определяет вероятность того, что электрон находится в данной точке 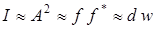 (см. Лекция 9).
(см. Лекция 9).
5) Электрон образует вокруг ядра заряженное "облако", пространственная плотность которого в некоторой точке соответствует интенсивности волны в данном месте.
6) На узловых поверхностях (совокупность всех узловых точек стоячих волн см. "Механика . . . ". Лекция 7) интенсивность волны и соответствующая вероятность обнаружить там электрон, равны нулю.
| <== предыдущая страница | | | следующая страница ==> |
| на входе регистр | | | Звуковые волны |
Дата добавления: 2014-08-09; просмотров: 785; Нарушение авторских прав

Мы поможем в написании ваших работ!