Звуковые волны

1.1.1. История акустики.

Акустика является разделом физики, а конкретно, разделом механики, который занимается либо теорией колебаний механических систем различной степени сложности, либо теорией волновых процессов, связанных с распространением звуковых волн в реальных средах. Акустическая волна (звуковая волна) есть процесс распространения деформаций в пространстве и во времени. Звуковые волны распространяются только в среде и не распространяются в вакууме.

Одно из первых упоминаний о существований звука под водой содержится в записной книжке Леонардо да Винчи. В 1490 году он писал: «Если вы остановите свой корабль и опустите один конец длинной трубы в воду, а другой её конец приложите к уху, то вы услышите корабли на большом расстоянии от вас».

К числу первых работ по акустике следует отнести работы голландского физика Снеля (1620г.), который впервые сформулировал закон отражения и преломления звуковых волн на границе раздела двух сред. В оригинальной формулировке он звучит так: отношение синуса угла падения к синусу угла преломления есть константа для данной границе раздела. В современной формулировке это отношение равно отношению скоростей звука в сопряженных средах, но во времена Снеля не было даже представления о том, что такое скорость звука!

Повторное открытие закона Снеля приписывают французскому учёному Декарту (1627г.), хотя сами французы считают Декарта первооткрывателем. Можно также отметить, что аналогичный закон отражения и преломления электромагнитных волн был сформулирован Френелем только в 1823г.

Первая теоретическая оценка скорости звука в атмосфере была дана Ньютоном (~1687г.) на основе кинетической теории газов и определялась как соответствующая изотермическому процессу деформирования воздушной среды 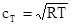, ( 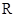- газовая постоянная, 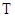- абсолютная температура). Авторитет Ньютона был настолько велик, что его оценку, которая оказалась ошибочной ( 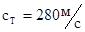) пересмотрели только после её экспериментального определения в 1738г. членами Парижской академии наук, а теоретическую оценку дал Лаплас (1782г.), который предложил считать процесс распространения звуковой волны адиабатическим, при этом 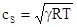, где 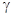- постоянная адиабаты.

Первая теоретическая работа по акустике была написана Л. Эйлером (1727г.)- действительным членом Российской академии наук: «Физическая диссертация о звуке». Л. Эйлер родился в Швейцарии и был приглашён в Российскую академию наук в 1726г. в возрасте 19 лет. За свою жизнь опубликовал свыше 800 научных работ, которые его ученики публиковали после его смерти в течение 80 лет, в том числе ~100 работ было написано только за 1770г, когда Л. Эйлер был уже слепым.

Первая экспериментальная работа по измерению скорости звука в атмосфере была выполнена в 1738г. На окраине Парижа на двух холмах были установлены пушки на расстоянии порядка 30км, которые стреляли навстречу друг другу. Световая вспышка в момент выстрела служила началом отсчёта времени, а в момент прихода звуковой волны измерялось время распространения. Для исключения влияния ветра результаты измерений на встречных трассах усреднялись. Эксперимент подтвердил правоту Лапласа и тот факт, что процесс распространения звуковой волны является адиабатическим. Это положение вошло в систему основных уравнений акустики. Другое основное уравнение- уравнение движения в акустике было сформулировано Л. Эйлером в 1765г.

Первая монография «Акустика» была написана немецким учёным Эрнстом Хладни (1802г.). В этой монографии автор дал систематизированное изложение теории колебаний стержней, мембран, пластин, музыкальных инструментов, а также методы визуализации колебаний (фигуры Хладни). На перевод монографии с немецкого языка на французский Наполеон выделил 6000 франков (для справки: жалование Наполеона, когда он был начинающим лейтенантом артиллерии, составляло 92 франка в месяц).

Особый интерес вызывают волны на воде, которые относятся к классу гравитационных волн. К тому же классу относятся внутренние волны в океане, волны плавучести в атмосфере и корабельные волны. Парижская академия наук учреждает приз за лучшую работу, посвящённую теории таких волн. В 1816г. этот приз выигрывает Коши в возрасте 25 лет, более известный нам как выдающийся математик.

Первая попытка измерения скорости звука в воде была предпринята французом Беданом (1820г.) вблизи Марселя, но плохая синхронизация измерений не позволила получить достоверные данные.

В 1826г. швейцарцы Шарль Штурм и Даниэль Колладон измерили скорость звука в воде на акватории Женевского озера, использовав в качестве излучателя подводный колокол, а в качестве приёмника – слуховую трубку с упругой мембраной на входе. Синхронизация измерений проводилась с помощью световой вспышки. Измеренное значение скорости звука 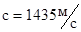оказалось достаточно точным с погрешностью 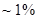. Слуховая трубка оказалась настолько удачным приёмником звуковых сигналов в воде, что нашла применение на Российском флоте для обнаружения шума миноносцев и торпедных катеров в условиях плохой видимости, что позволяло предупредить торпедную атаку кораблей, стоящих в бухте. Эта идея была высказана адмиралом Макаровым и успешно применялась на флоте.

В 1844г. англичанин Рассел наблюдал необычное явление-распространение вдоль Темзы одиночной волны, которую он сопровождал верхом на расстоянии порядка нескольких километров, причём волна распространялась без заметного изменения амплитуды и формы. В последствии такие одиночные волны были названы солитонами, а теория солитонов стала одним из перспективных разделов современной акустики и физики. Ближайшим аналогом солитона является волна цунами, скорость распространения которой зависит от длины волны 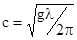( 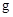- ускорение силы тяжести, 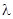- длина волны), сама зависимость 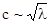была предсказана ещё Ньютоном.

Процесс собирания знаний по различным разделам акустики завершился выходом в свет в 1877г. фундаментальной работы Джона Вильяма Стретта, который за выдающиеся заслуги в науке получил титул лорда Рэлея (Рейли) – Теория звука т.т. 1,2. В последствии Рэлей был удостоен звания президента Британской академии Наук. Монография Рэлея содержит все основные разделы современной акустики: теорию колебаний систем с сосредоточенными параметрами с 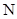степенями свободы, теорию колебаний систем с распределёнными параметрами – теорию колебаний стержней, мембран, пластин, теорию музыкальных инструментов и органов речи и слуха, теорию резонаторов и анализаторов спектра, а также обширные исследования по дифракции волн, теории волноводов, теории излучения звука, архитектурной акустике.

Практическая гидроакустика начинается с открытия в 1880г. братьями Кюри пьезоэффекта, а уже в 1916г. Ланжевен (Франция) и Шиловский (Россия) получают патент на первый гидролокатор (излучатель Ланжевена) на основе сегнетовой соли (или кварца).

Первый звуковой эхолокатор, предназначенный для работы в воздухе был запатентован Ричардсоном (Англия) в 1912г. через 5 дней после гибели «Титаника», а через месяц он получил патент на аналогичное устройство, работающее в воде.

Фесенден (США) сконструировал электродинамический излучатель, предназначенный для эхо-локации под водой. В 1914г. гидролокатор с таким излучателем позволял обнаруживать айсберги на расстоянии до 2 миль ( 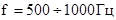), а в первую мировую войну такие излучатели использовались для акустической связи между ПЛ.

1916г.-гидролокатор Ланжевена и Шиловского позволял обнаруживать ПЛ на расстоянии ~1мили.

1935г.¸38г. – разработка шумопеленгаторов для обнаружения ПЛ. Шумопеленгатор JP (линейная антенна, усилитель, полосовой фильтр, наушники =5000$) – основной шумопеленгатор времён II мировой войны, с помощью которого были была выиграна война с немецкими ПЛ в Атлантике.

1937г. – Спилхауз разработал первый батитермограф, позволявший измерять температуру верхних слоёв морской воды, которым снабжались НК ВМФ для учёта рефракции звука и «послеполуденного эффекта» - отклонения звуковых лучей вглубь моря после прогрева верхних слоёв моря, нарушавшего связь.

Первые эксперименты по созданию отечественного гидролокатора были начаты В.Н. Тюлиным в 1924г. и завершились созданием первой ГЛС «Тамир» в 1940г., которая была базовой ГЛС для подводных кораблей и ПЛ во время войны.

В 1928г. С.Я. Соколов разработал пьезокварцевые излучатели мощностью 600Вт для новых гидроакустических антенн с дальностью действия 5¸10км. (совместно с В.И. Тюлиным). За работы в области гидроакустики стал Лауреатом Государственной премии (1942г.). Автор первой отечественной монографии «Основы электроакустики», автор первого ультразвукового дефектоскопа, первой системы подводного звуковидения в непрозрачных средах – Лауреат Государственной премии 1951г., основатель кафедры электроакустики в ЛЭТИ (1931г.).

В 1941г. вышел первый фундаментальный труд по гидроакустике – В.Н. Тюлин: «Гидроакустика». Акустический институт (АКИН) создан в 1953г. на базе акустической лаборатории ФИАН. «Акустический журнал» - журнал АН СССР, издаётся с 1955г.

1.1.2. Разделы акустики и их взаимосвязь.

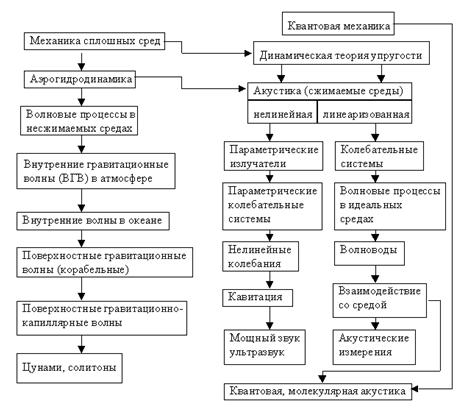Какая-либо классификация современной акустики на отдельные разделы крайне затруднена большим разнообразием вопросов, лежащих в сфере её интересов, и взаимосвязью различных разделов либо на основе общности основных уравнений, либо на основе общности применяемых методов анализа.

Основу классической акустики составляют уравнения и понятия механики сплошных сред, которые обычно подразделяются на уравнения аэрогидродинамики, описывающие движение жидких и газообразных сред, и уравнения и понятия динамической теории упругости, описывающие движение в деформируемых твёрдых телах.

Основу квантовой и молекулярной акустики составляют уравнения и понятия квантовой механики, учитывающие дискретную природу вещества и специфические квантовые эффекты. Граничной между представлениями классической и квантовой акустики является частота Дебая 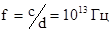(с – скорость звука в твёрдом теле, d – межатомное расстояние в кристаллической решётке).

Основные уравнения акустики являются нелинейными, что сильно затрудняет их применение в общем случае и оправдывает в свою очередь некоторые приближения. Так, например, если пренебречь сжимаемостью среды, т.е. акустическими эффектами, то мы получим более простые уравнения, описывающие целый ряд волновых явлений, происходящих либо в атмосфере (внутренние гравитационные волны), либо в океане (внутренние волны), либо на поверхности воды (поверхностные корабельные волны, гравитационно-капиллярные волны). Самыми яркими представителями нелинейных волновых процессов являются уединенные (одиночные) волны - солитоны, открытые Расселом в 1844г., хотя более страшные их представители – волны цунами были известны гораздо раньше.

Если в основных уравнениях акустики пренебречь всеми нелинейными членами, т.е. выполнить при определённых условиях так называемую линеаризацию, то мы получим классическую линейную акустику, в рамках которой рассматривается большая часть всех вопросов, представляющих как теоретический, так и практический интерес. Именно эти разделы акустики проработаны наиболее глубоко и всесторонне и составляют традиционную линейную акустику. В рамках линейной акустики можно выделить как самостоятельные разделы теорию колебаний (имеются в виду акустические колебательные системы) и теорию волновых процессов.

В теории колебаний рассматриваются системы с сосредоточенными параметрами с N-степенями свободы, предельным случаем которых являются системы с распределёнными параметрами (стержни, концентраторы, мембраны и пластины, цилиндры и произвольные оболочки). Модельные колебательные системы могут быть либо линейными (одномерными), либо плоскими, либо трёхмерными (объёмными).

Наиболее сложными в описании являются произвольные трёхмерные колебательные системы с распределёнными параметрами на основе электроупругих сред (пьезокерамических материалов). Каждая колебательная система характеризуется спектром собственных (резонансных) частот и набором соответствующих им собственных функций или мод колебаний.

Характерная особенность колебательного процесса – преобразование энергии из потенциальной в кинетическую и наоборот, а также диссипация энергии при наличии потерь. Волновые процессы имеют место в неограниченных средах, однородных, неоднородных либо анизотропных (например, в кристаллах). Каждая волна характеризуется геометрией волнового фронта (плоские, цилиндрические, сферические волны), скоростью распространения в направлении нормали к волновому фронту и законом ослабления амплитуды волны с расстоянием. В рамках волнового описания строится теория излучения акустических волн и теория дифракции, теория направленного излучения и приёма, изучаются законы отражения и преломления звуковых волн на простейших границах раздела, плоских, статистически шероховатых, либо содержащих малые периодические неровности, законы рефракции в неоднородных средах.

Характерная особенность волнового процесса – перенос энергии в направлении распространения волны с некоторой скоростью, называемой групповой скоростью, строго ограниченной сверху. В отличие от неё скорость распространения волнового фронта, называемая фазовой скоростью, может быть любой.

Теория волноводов является сравнительно молодым разделом акустики, который быстро набирает силу. Достаточно сказать, что эта теория имеет прочные позиции и в атмосферной акустике, и в гидроакустике, и в геологии, а также на стыке этих дисциплин (например, в морской геологии). Более простыми свойствами обладают модельные волноводы с идеальными границами, заполненные однородной идеальной средой, жидкой либо газообразной. Наиболее сложными свойствами обладают многослойные либо неоднородные волноводы с импедансными границами, регулярными либо нерегулярными.

Характерная особенность волнового процесса в волноводе – наличие спектра собственных значений для постоянной распространения и соответствующих функций поперечного сечения, которые в совокупности характеризуют нормальную волну как элементарную форму волнового процесса в волноводе.

Изучение взаимодействия звуковых волн со средой восходит к классическим работам Стокса и Киргоффа, которые дали оценку поглощения звука в среде при учёте вязкости и теплопроводности. Эти механизмы поглощения имеют место на любых частотах. Однако, наибольший интерес представляют механизмы аномального поглощения звука с частотной зависимостью резонансного либо релаксационного типа. Наиболее интересны механизмы, происходящие на молекулярном либо квантовом уровне, а также механизмы, приводящие к усилению звука, например, в пьезополупроводниках.

Нелинейные эффекты в акустике обычно малы, но их влияние приводит к качественно новым эффектам, которые и представляют обычно наибольший интерес. Так, например, коэффициент нелинейного преобразования по мощности в параметрических излучателях составляет 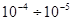, но этого достаточно для практического их использования в прикладной гидроакустике. Нелинейные эффекты в колебательных системах могут приводить к потере устойчивости самой колебательной системы и разрушению. В основе кавитации также лежат нелинейные процессы, приводящие к схлопыванию воздушных пузырьков, растворённых в воде, при прохождении звуковой волны, а сам процесс схлопывания сопровождается образованием мощных ударных волн, разрушающих металл.

Нелинейная акустика – наименее изученный раздел акустики, но и самый перспективный, т.к. реальные процессы всегда являются скорее нелинейными, чем линейными.

1.1.3. Общие характеристики звуковых процессов.

К общим характеристикам произвольных звуковых процессов относят частотный и динамический диапазоны.

Частотный диапазон чрезвычайно широк и условно подразделяется на четыре поддиапазона:

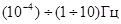- инфразвуковые колебания

Сюда относятся сейсмические колебания, связанные с движением (пульсациями) Земли как единого осциллятора с периодом 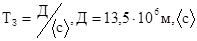- средняя скорость звука в Земле 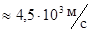. 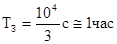, процессы, связанные с колебаниями гидросферы, которые порождают внутренние волны в океане и шельфовой зоне, модулирующие звуковые поля. Внутренние волны характеризуются частотой Брента-Вяйсяля:

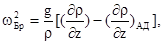
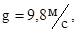
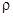- плотность, .

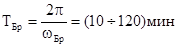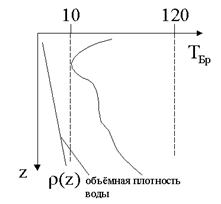Частота Брента-Вяйсяля имеет характерное распределение по глубине моря. Периоды внутренних волн лежат в диапазоне 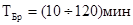, а также включают полусуточные и суточные периоды, связанные с поверхностным приливом.

Сюда же относятся колебания, связанные с вибрациями зданий и механизмов, шумовые процессы, строительные шумы, сейсмические шумы, шумы моря.

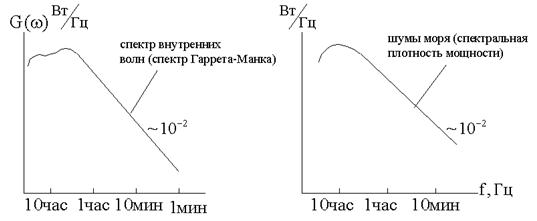
Шумовые процессы в море (шумы моря) и внутренние волны в океане характеризуются близкими по сути спектральными портретами.

Спектральная плотность мощности внутренних волн (спектр Баррета-Манка) и шумов моря имеют сходные частотные зависимости .

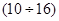Гц.¸ 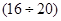кГц. – звуковые колебания, т.е. колебания, воспринимаемые человеческим ухом: звуковая акустика (электроакустика), гидроакустика, биоакустика, мощный ультразвук и ультразвуковая обработка материалов, рыбопоисковая техника, акустические приборы сейсморазведки и сейсмопрофилирования, томография океана.

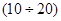кГц.¸ 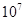Гц. – ультразвук: ультразвуковая техника и ультразвуковая дефектоскопия, интроскопия и звуковидение , медицинская диагностика и ультразвуковая томография, верхний диапазон гидроакустики (гидролокаторы бокового и секторного обзора, доплеровские лаги, профилографы, измерители скорости течений).

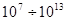Гц. – гиперзвук: физическая акустика, взаимодействие звука с веществом, молекулярная акустика, усиление гиперзвука в пьезополупроводниках, активные СВЧ-линии задержки.

Динамический диапазон также чрезвычайно широк, а для его сжатия применяют логарифмическую шкалу или уровень в децибеллах.

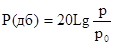- логарифмический уровень в децибеллах.

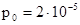Па – порог слышимости человеческого уха (0 дб).

Для воздушной среды при 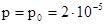Па амплитуда колебательной скорости частиц среды 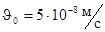, интенсивность звука .

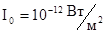20дб – тикание часов,

40дб – тихий разговор,

60дб – шум автомобиля,

80дб – громкий крик,

100дб – отбойный молоток (R~1м),

120дб – болевой порог уха (~20Па),

140дб – шум реактивного самолёта (R~100м),

180дб – шум реактивного самолёта (R~1м),

80¸90шум большого города (Нью-Йорк, Каир),

- шум в деловой части города,

200¸240дб – уровни мощных гидроакустических излучателей (взрывчатые источники и пневмопушки),

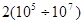Па= 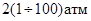. Общий диапазон: 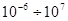Па (260дб). В иностранной литературе в качестве уровня отсчёта используют 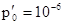Па (1 микропаскаль), .

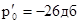1.2. Основные положения.

1.2.1. Основные уравнения акустики в жидких и газообразных средах.

Звуковое поле описывается следующим набором величин:

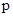- звуковое (избыточное) давление,

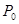- давление в невозмущённой среде,

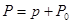- суммарное давление в возмущённой среде,

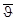- вектор колебательной скорости,

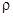- плотность среды.

Уравнение движения записывается в виде уравнения баланса сил инерции и внешних сил, действующих через поверхность, ограничивающую произвольный объём, а в идеальной среде все силы, действующие через поверхность, являются нормальными:

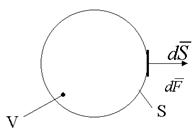
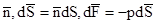
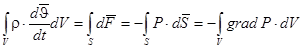
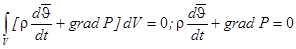- уравнение Эйлера (уравнение движения) (1.1.)

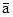- постоянный вектор,

,

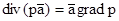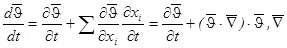- оператор Набла,

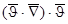- переносное ускорение,

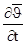- локальное ускорение.

Уравнение неразрывности выводится из условия сохранения массы:

, ,

,

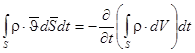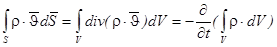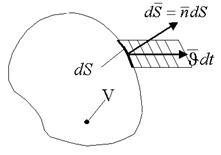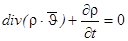- уравнение неразрывности (1.2.)

В качестве третьего уравнения берут обычно уравнение состояния, связывающее давление и плотность. Считается, что процесс распространения звуковой волны является адиабатическим:

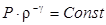- уравнение адиабаты, 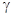- показатель адиабаты (1.3.)

для газов: 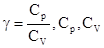- теплоёмкость при постоянном давлении или объёме. 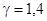-для воздуха, 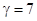- для воды.

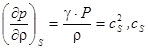- адиабатическая скорость звука в воздухе (1.4.)

Для жидких сред скорость звука вводят через адиабатическую сжимаемость:

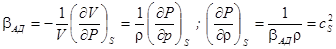
В качестве других форм уравнения состояния используют разложение вида:

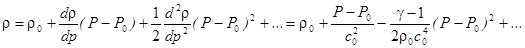
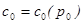- скорость звука в невозмущённой среде.

;

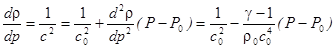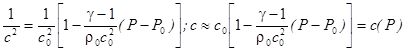
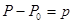- избыточное (звуковое) давление,

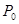- давление в невозмущённой среде (атмосферное, гидростатическое).

Уравнения (1.1.), (1.3.) образуют замкнутую (полную) систему уравнений акустики относительно величин: 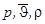, описывающих звуковое поле, все уравнения являются нелинейными.

1.2.2. Линеаризация. Волновое уравнение.

Условия линеаризации означают, что параметры среды, возмущённые звуковой волной, мало отличаются от параметров невозмущённой среды :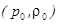

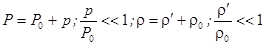
Третье условие, записанное в форме:

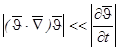сводится к условию .

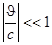Все три условия линеаризации хорошо выполняются за исключением отдельных случаев, когда звуковое давление соизмеримо с атмосферным или гидростатическим (мощные излучатели).

Система линейных уравнений акустики имеет вид:

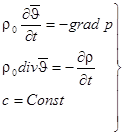
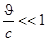(1.5.)

Решение системы (1.5.) сводят к решению одного уравнения более высокого порядка, используя представление векторного поля 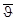через градиент скалярного поля:

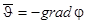, где 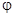- потенциал скорости. (1.6.)

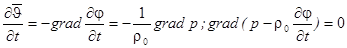
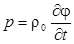
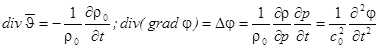
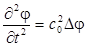волновое уравнение для потенциала скорости (1.7.)

Для гармонических процессов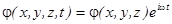

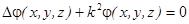- уравнение Гельмгольца. (1.8.)

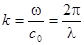, - длина волны и волновое число.

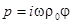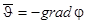, (1.9.)

Иногда волновое уравнение записывается в форме:



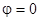
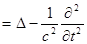 - оператор Даламбера.

Таким образом, решение системы уравнений (1.5.) сведено к решению уравнения Гельмгольца (1.8.) (или в более общем случае к решению уравнения (1.7.)), а затем по формулам (1.9.) находятся поле давления и векторное поле колебательной скорости .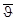

1.2.3. Обобщение на вязкие среды.

В вязкой среде скалярное поле давления дополняется тензорным полем вязких напряжений :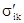

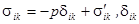- символ Кронекера,

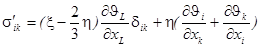(1.10.)

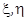- первая (объёмная) и вторая (сдвиговая) вязкости.

Выражение (1.10.) является полным аналогом закона Гука в тензорной форме:

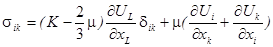
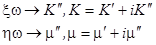
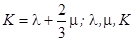- постоянные Лямэ и модуль всестороннего сжатия (объёмный модуль).

Учёт потерь в твёрдом теле сводится к введению комплексных модулей упругости:

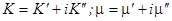, тогда мнимые добавки 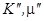формально являются аналогом коэффициентов вязкости, а именно 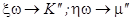, т.е. движение вязкой жидкости, в которой появляется сдвиговая упругость, аналогично поведению твёрдого тела.

Уравнение движения имеет вид:

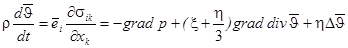(1.11.)

и называется уравнением Навье-Стокса.

Для потенциального поля скоростей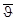

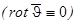
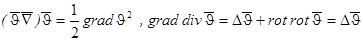
и уравнение движения принимает вид:

(1.12.)

После линеаризации уравнения (1.12.) векторное поле скорости 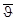опять допускает представление через градиент скалярного поля 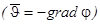, а для потенциала 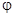можно получить уравнение:

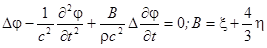(1.13.)

При гармонической зависимости от времени уравнение (1.13.) сводится к уравнению Гельмгольца:

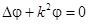
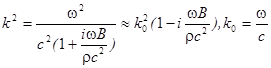
В этом уравнении волновое число 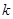оказывается комплексным и допускает представление:

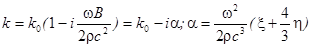- коэффициент затухания звука в вязкой среде (1.14.)

Таким образом, формальный учёт вязкости сводится к тому, что в уравнении Гельмгольца достаточно обобщить волновое число по формуле (1.14.).

Условием применимости такого подхода является неравенство 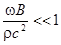, которое обычно хорошо выполняется.

Формальный учёт потерь на теплопроводность среды сводится к обобщению вида (Стокс):

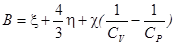, где 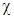- коэффициент теплопроводности.

1.2.4. Основные уравнения акустики в твёрдых телах.

В отличие от жидких и газообразных сред, в которых силовое поле есть скалярное поле давления, а все деформации есть деформации всестороннего сжатия-растяжения (объёмные деформации), в твёрдом теле силовое поле и поле деформаций носят более сложную тензорную природу и описываются соответственно тензором напряжений и тензором деформаций. Связь между этими тензорами описывается законом Гука.

Произвольное движение твёрдого тела описывается вектором смещения 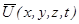, но в акустике деформируемого твёрдого тела рассматривают только такие движения, которые связаны с изменением расстояния между двумя соседними точками .

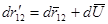Произвольная линейная зависимость между векторам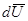и и 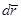описывается с помощью компонент производного тензора 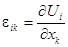, имеющего в общем случае девять компонент: .

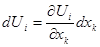Тензор деформаций определяется как симметричная часть производного тензора

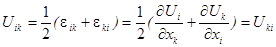, тогда как антисимметричная его часть определяет вихревой вектор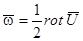

,

,

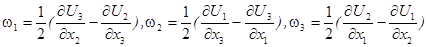причём такое представление единственно:

.

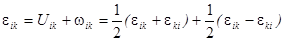Диагональные компоненты тензора деформаций характеризуют деформации сжатия-растяжения вдоль соответствующих осей, симметричные недиагональные компоненты – деформации искажения формы, а вихревой вектор 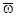характеризует вращение элементарного объёма твёрдого тела вокруг мгновенной оси.

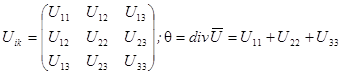- объёмная деформация.

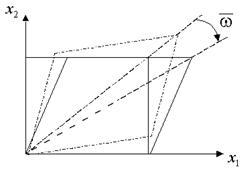
В качестве простейшего примера рассмотрим деформацию чистого сдвига (плоскую), которая описывается следующим образом:

,

,

, , .

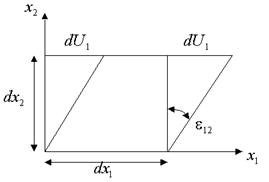
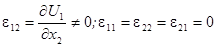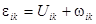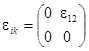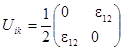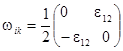Сама деформация чистого сдвига распадается на две составляющие: деформацию искажения квадрата в ромб без изменения площади и чистое вращение без деформации вокруг оси на угол .

В отличие от жидких сред силовое поле в твёрдом теле не описывается скалярным полем давления, а силы действующие на произвольный элемент поверхности, не являются нормальными. Произвольная линейная зависимость между векторам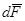и и 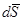описываются с помощью компонент производного тензора 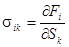, имеющего в общем случае девять компонент, однако, из условия равновесия при деформировании малого элементарного объёма следует симметричность производного тензора, который называют тензором упругих напряжений:

; .

.

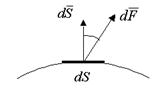
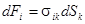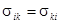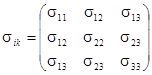Диагональные элементы тензора напряжений описывают напряжения сжатия-растяжения (нормальные), тогда как недиагональные элементы описывают сдвиговые напряжения (касательные).

Используется также матричная форма записи компонент тензора деформаций и тензора напряжений:

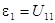
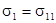
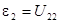
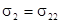
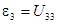
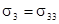
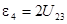
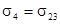
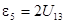
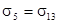
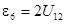
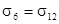
Тензор напряжений определяется через компоненты тензора деформаций обобщённым законом Гука:

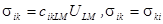, где: 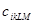- тензор упругих постоянных.

Тензор упругих постоянных 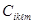симметричен относительно следующих операций:

,

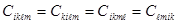что является следствием симметрии тензора напряжений 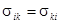и тензора деформаций 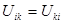. С учётом свойств симметрии тензор 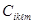имеет из 81 составляющей только 21 независимые составляющие.

Наибольшим количеством упругих постоянных характеризуются упругие свойства наименее симметричных кристаллов – 21.

Наименьшее количество упругих постоянных соответствует изотропному твёрдому телу – 2.

По свойствам симметрии кристаллы образуют следующие семь кристаллографических систем (сингоний):

1. Триклинная -21 постоянная

2. Моноклинная -13

3. Орторомбическая -9

4. Тетрагональная -7 или 6

5. Тригональная -6

6. Гексагональная -5, (металлы)

7. Кубическая -3 ( )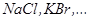

Так, например, пьезокварц относится к тригональной кристаллографической системе, а поляризованная пьезокерамика – к гексагональной.

Для изотропного тела закон Гука принимает более простой вид:

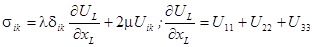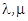, - постоянные Лямэ. (1.15.)

Используется также матричная форма записи закона Гука :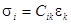

.

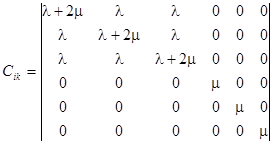Уравнение движения для произвольного объёма твёрдого тела выводится из условия баланса сил инерции и упругих сил, действующих через поверхность, ограничивающую объём:

,

,

,

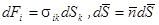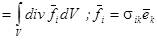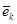- тройка единичных векторов.

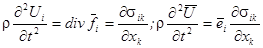. (1.16.)

Подстановка в (1.16.) закона Гука (1.15.) даёт уравнение движения в форме:

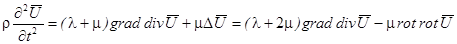. (1.17.)

Уравнение (1.17.) не является волновым, но допускает разбиение на два волновых уравнения, которые проще исходного уравнения.

Для этого вводят скалярный и векторный потенциалы в силу единственности разбиения произвольного векторного поля на пару составляющих:

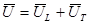, таких что .

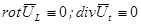В силу этого составляющая 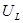(продольная) представима градиентом скаляра, а составляющая 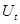(поперечная) представима ротором некоторого вектора:

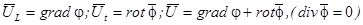, (1.18.)

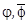- скалярный и векторный потенциалы.

Справедливы следующие способы разбиения исходного уравнения на пару волновых:

,

,

,

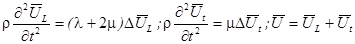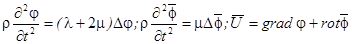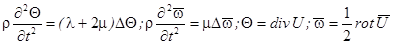где: 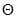- объёмная деформация .

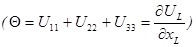При гармонической зависимости от времени волновые уравнения переходят в соответствующие уравнения Гельмгольца:

,

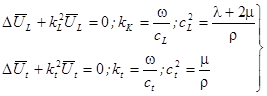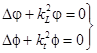
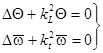, (1.19.)

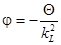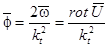, , где: 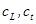- скорости продольных и поперечных волн.

Разбиение исходного уравнения на пару волновых ещё не означает независимого существования продольных и поперечных волн и в большинстве случаев они образуют связанную комбинацию.

1.2.5. Акустические характеристики среды распространения.

Важнейшими характеристиками среды являются плотность 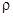, скорость звука 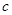или скорости продольных и поперечных 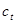волн, а также коэффициенты поглощения звука 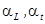, если учитываются потери на распространение в реальной среде. Как правило, при рассмотрении волновых процессов, происходящих в ограниченных объёмах, плотность и скорость звука являются некоторыми константами. При рассмотрении глобальных процессов, происходящих, например, в земной атмосфере, в океане или земной коре, необходимо учитывать пространственную изменчивость акустических характеристик среды распространения.

Атмосферная акустика.

В земной атмосфере давление и плотность имеют существенную вертикальную изменчивость, упорядоченную силами гравитации, и связаны уравнением состояния, скорость звука также является сложной функцией высоты:

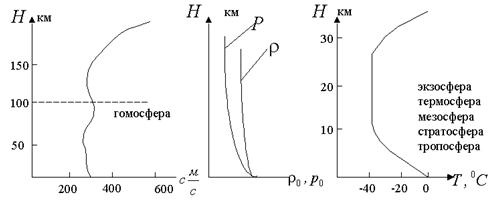Для адиабатической атмосферы 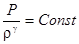плотность и давление (атмосферное) изменяются по закону:

, ,

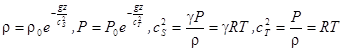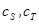- адиабатическая и изотермическая скорости звука, 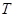- абсолютная температура, 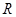- газовая постоянная, однако, реальное состояние атмосферы не является строго адиабатическим. Неоднородность атмосферы по скорости звука приводит к рефракции звуковых лучей. В пределах гомосферы ( 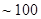км.) состав атмосферы постоянен ( 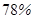-азот, 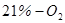, 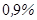-аргон), в гетеросфере состав меняется и преобладающими становятся гелий и водород.

Гидроакустика.

Неоднородность морской среды по скорости звука также весьма существенна, хотя её плотность меняется незначительно из-за малой сжимаемости воды. Существует множество эмпирических формул, описывающих изменчивость скорости звука в зависимости от температуры 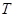, давления 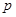и солёности 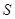, простейшая из них была предложена Вудом:

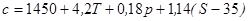, где 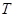измеряется в 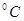, 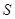- в промиллях 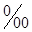, 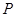- в атмосферах, скорость в .

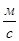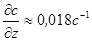- градиент скорости вблизи дна, 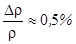в той же точке.

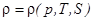- уравнение состояния.

Сложная зависимость скорости звука от параметров 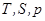, характеризуемая профилем вертикального распределения скорости 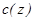, приводит к рефракции звуковых лучей, а в некоторых случаях к формированию подводного звукового канала (ПЗК) или приповерхностного звукового канала (ППЗК).

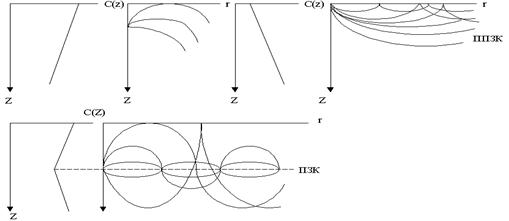Геоакустика.

Наиболее сложным оказывается распределение скорости звука, продольной и поперечной составляющих, в земной коре, мощность которой составляет 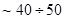км. Как правило, с увеличением глубины плотность пород, слагающих земную кору, растёт, растут и скорости звука 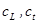с градиентом .

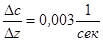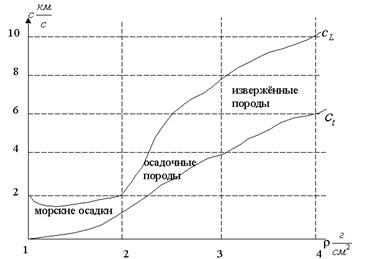
Методами сейсмической томографии выявлена и акустическая структура Земли с характерным распределением скоростей с глубиной.

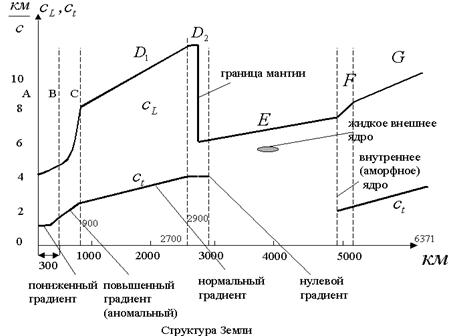Оболочка А состоит из ОС - осадочного слоя, МС – метаморфического слоя, ПС – промежуточного слоя, ГС – гранитного слоя, БС –базальтового слоя. - граница Мохоровича , - техносфера.

Оболочка В 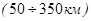- подкорковая зона (верхняя мантия), 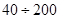– зона Булленса (ВМСБ), слой Гутенберга 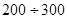км. (ВМСГ), пониженные .

Оболочка С 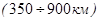- переходная зона аномального возрастания скоростей , средняя мантия (слой Голицына).

Оболочка 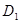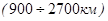- зона нормального возрастания скоростей 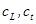за счёт давления, слой Вихерта (1896г.).

Оболочка 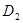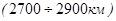- зона постоянных скоростей 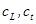(пограничная зона).

Оболочка Е 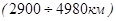- внешнее жидкое ядро.

Оболочка 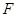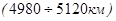- затвердевающий слой ядра.

Оболочка G 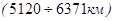- твёрдое ядро.

Лунный грунт

Наиболее экзотическими оказались акустические характеристики лунного грунта. Верхний слой мощностью 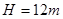образует зону малой скорости с параметрами: 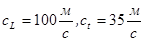и высокой добротностью 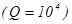, тогда как нижележащие слои характеризуются постоянством параметров 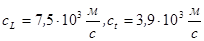вплоть до глубины 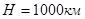(мантия).

Максимальные и минимальные значения скорости звука приведены в таблице:

газы	жидкости	тв. тело
лунный грунт	алмаз	луна
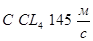
	фреон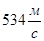
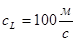
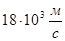
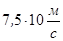
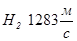
	глицерин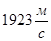

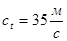
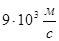
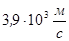
Водолазы используют гелиевые смеси с высокой скоростью звука, что приводит к искажениям речи, т.к. спектр собственных частот органов речи повышается.

1.2.6. Простейшие типы волн.

Простейшими типами волн являются решения уравнения Гельмгольца (1.8.) в основных системах координат: прямоугольной, сферической и цилиндрической, которые называются соответственно плоской, сферической и цилиндрической волнами.

Плоская волна.

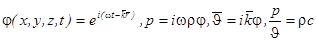, где 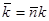волновой вектор, 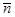- единичный вектор нормали к волновому фронту, 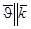, что означает, что волна является продольной. 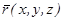- радиус-вектор в точке наблюдения. Характерная особенность плоской волны – синфазное изменение давления и колебательной скорости 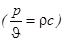, 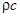- волновое сопротивление.

Сферическая волна.

,

.

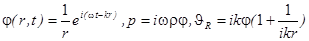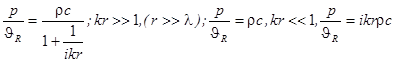Амплитуда сферической волны убывает по закону 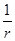, что соответствует сферической расходимости волнового фронта. Давление и колебательная скорость синфазны только на больших расстояниях 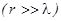. На малых расстояниях они сдвинуты по фазе на 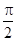, что является признаком реактивного поля.

Колебательная скорость на малых расстояниях убывает по закону 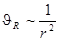, что соответствует движению несжимаемой жидкости и также является признаком реактивности ближнего поля .

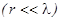Цилиндрическая волна.

,

,

.

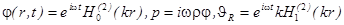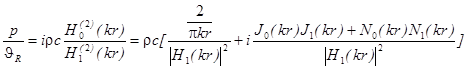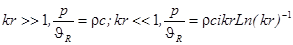Амплитуда цилиндрической волны убывает по закону 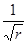, что соответствует цилиндрической расходимости волнового фронта. Давление и колебательная скорость синфазны только на больших расстояниях 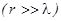. На малых расстояниях они сдвинуты по фазе на 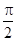, что является признаком реактивного поля.

Колебательная скорость на малых расстояниях убывает по закону 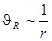, что соответствует движению несжимаемой жидкости и также является признаком реактивности ближнего поля .

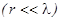1.2.7. Плоские волны в твёрдом теле.

Для выяснения условий существования плоских волн в твёрдом теле нужно взять уравнение распространения в форме (1.17.):

,

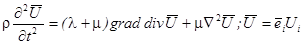- тройка единичных векторов.

Решение типа плоской звуковой волны имеет вид:

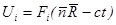, где: 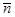- единичный вектор в направлении распространения, 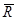- радиус вектор в точку наблюдения, 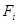- произвольная функция аргумента .

,

,

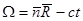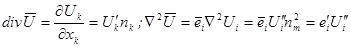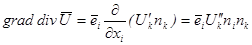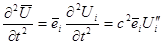. (1.20.)

Подставляя (1.20.) в уравнение распространения, получаем следующую систему уравнений:

.

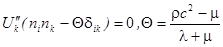Определитель системы 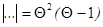имеет простой корень 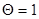, которому соответствует продольная волна 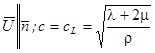и кратный корень 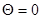, которому соответствует две поперечные волны, для которых вектор смещения лежит в плоскости, перпендикулярной , .

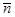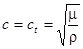Частный случай:

,

.

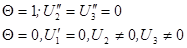Аналитическая запись:

,

,

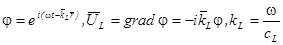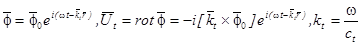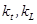- волновые числа, соответствующие продольной и поперечной волнам.

Основные характеристики волнового процесса.

· геометрия волнового фронта (плоская волна, сферическая, цилиндрическая, …)

· направление распространения, заданное волновым вектором ,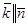

· скорость распространения в направлении 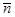, равная скорости звука в среде,

· длина волны 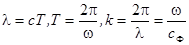- постоянная распространения,

· тип волны: .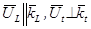

Следует также различать:

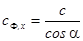- фазовая скорость в направлении оси х, 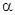- угол скольжения относительно оси . , ,

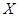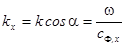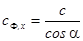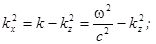
<== предыдущая страница | следующая страница ==> Многоэлектронные атомы | Исследование систем управления организацией Дата добавления: 2014-08-09; просмотров: 1446; Нарушение авторских прав Поделиться с ДРУЗЬЯМИ: Мы поможем в написании ваших работ!