
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Нелинейные цепи: электрические и магнитные цепи постоянного тока
Обычно электрические цепи содержат нелинейные элементы: резистивные, индуктивные и емкостные, описываемые вольт- амперными I(V), вебер-амперными ψ(i), и кулон- вольтными q(UC) характеристиками.
| I |
| ψ |
| q |
| U |
| IL |
| UC |
Нелинейные свойства могут искажать форму токов, а могут и лежать в основе принципа действия, например, выпрямителей, стабилизаторов, усилителей.
Включение нелинейного резистора в произвольную линейную цепь.
Цепь постоянного тока
| I(U) |
| ЕЭК |
| RЭК |
| U |
| I |
| I |
| U |
| (Eэк-U)/Rэк |
| A |
| Ia |
| Ua |
| Eэк |
| Еэк/Rэк |
Нагрузочная характеристика активного двухполюсника:I=(Eэк-U)/Rэк
Точка пересечения А нагрузочной характеристики активного двухполюсника и ВАХ нелинейного элемента определяет рабочий режим цепи, а графоаналитический метод расчета нелинейной цепи- метод нагрузочной характеристики.
Последовательное соединение нелинейных элементов в цепи переменного тока
Точка А решение задачи
| RЭК |
| ЕЭК |
| I |
| U2 |
| U1 |
| U |
| I |
| U |
| I(U1) |
| I(U2) |
| U2 |
| U1 |
| U1+U2 |
| I(U1+U2) |
| A |
| (Eэк-U)/Rэк |
Параллельное соединение нелинейных элементов
| Rэк |
| Еэк |
| I1(U) |
| I2(U) |
| U |
| I |
| I1 |
| I2 |
| I1U)+I2(U) |
| I1(U) |
| I2(U) |
| U |
| A |
| (Eэк-U)/Rэк |
Точка А решение задачи
Смешанное соединение нелинейных элементов.
| Еэк |
| Rэк |
| I1 |
| I3 |
| I2 |
| U |
| U1 |
| I1(U-U1) |
| I2(U1) |
| I3(U1) |
| U1 |
| I2(U1)+I3(U1)=I1 |
| I1 |
| U |
| U |
| I1 |
| I1(U)=I2(U1)+I3(U1)+I1(U-U1) |
| I3 |
| I2 |
| A |
| (Eэк-U)/Rэк |
Точка А – решение задачи.
Метод двух узлов
На предыдущих трех рисунках получения эквивалентной ВАХ последовательного, параллельного и смешанного соединения нелинейных элементов приведены решения задачи определения тока и напряжения в двух узлах 1 и 2.
| Rэк |
| Еэк |
| R |
| U |
| I |
| U |
| I |
| A |
| ВАХ |
| (Eэк-U)/Rэк |
Графическим решением задачи является точка А пересечения ВАХ эквивалентной нагрузки с внешней характеристикой эквивалентного источника ВАХ=(Eэк-U)/Rэк.
Этот метод решения задачи называется методом двух узлов.
Понятно, что это решение может быть получено и аналитически.
Линеаризация нелинейного сопротивления.
Расчет нелинейных цепей удобно вести в рамках линейных приближений характеристик нелинейных сопротивлений (при малых отклонениях от рабочей Р),
То есть заменой нелинейного резистора линейным.
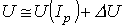
где 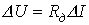 (закон Ома для малых приращений);
(закон Ома для малых приращений);
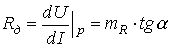 -дифференциальное сопротивление.
-дифференциальное сопротивление.
| Р |
| U |
| I |
| α |
Линеаризованные схемы замещения.
Если исходный режим определен и требуется рассчитать, лишь приращения токов и (или) напряжений, обусловленные изменением напряжения или тока источника, целесообразно использовать эквивалентные схемы для приращений, получаемые на основании законов Кирхгофа для малых приращений:
-первый закон Кирхгофа: 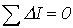 ;
;
-второй закон Кирхгофа: 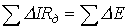 .
.
При составлении схемы для приращений:
1) все ЭДС и токи источников заменяются их приращениями;
2) нелинейные резисторы заменяются линейными с сопротивлениями, равными дифференциальным в рабочих точках.
Необходимо помнить, что полная величина какого-либо тока или напряжения в цепи равна алгебраической сумме исходного значения переменной и ее приращения, рассчитанного методом линеаризации.
Если исходный режим работы нелинейного резистора неизвестен, то следует задаться рабочей точкой на его ВАХ и, осуществив соответствующую линеаризацию, произвести расчет, по окончании которого необходимо проверить, соответствуют ли его результаты выбранной точке. В случае их несовпадения линеаризованный участок уточняется, расчет повторяется и так до получения требуемой сходимости
Магнитные цепи при постоянном магнитном потоке
Эрстед в 1820г. продемонстрировал, что вблизи проводника с током возникает магнитное поле.
Магнитная цепь-совокупность различных ферримагнитных и неферромагнитных устройств для создания магнитных полей нужных конфигураций и интенсивности.
Различают неразветвленные и разветвленные магнитные цепи. В общем случае магнитная цепь нелинейная.
Закон полного тока для магнитной цепи.
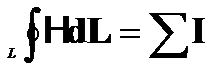
Интеграл от напряженности магнитного поля по любому замкнутому контуру равен алгебраической сумме токов, сцепленных с этим контуром.
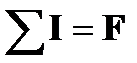 -магнитодвижущая сила (МДС)-[Ампер]
-магнитодвижущая сила (МДС)-[Ампер]
Н-[А/m]-напряженность магнитного поля.
Для магнитного поля, возбужденного катушкой с током I с w витками:
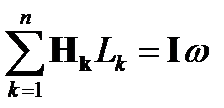
| I1 I2 I3 I4 |
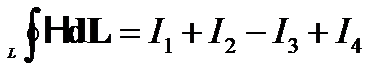
|
| H |
| L |
По аналогии с электрическими цепями существуют неразветвленные и разветвленные магнитные цепи.
Неразветвленная магнитная цепь
Магнитной цепью в электротехнических устройствах называют путь, по которому распространяются и замыкаются магнитные линии. Цепи образуют магнитные системы. Задачей расчета неразветвленной магнитной цепи в большинстве случаев является определение МДС F= Iω, необходимой для того, чтобы получить заданные значения магнитного потока Ф или магнитной индукции В в некотором участке магнитопровода (чаще всего в воздушном зазоре).
Если на магнитопроводе расположено к катушек, то МДС определится, как сумма МДС отдельных катушек: 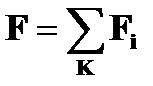
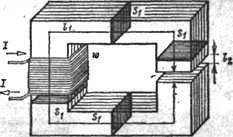
В воздушном зазоре магнита магнитная индукция В2 [T] связана с напряженностью Н2 простым отношением В2= μ Н2 (μ- магнитная проницаемость вещества в зазоре). В ферромагнетике В1=μ1 Н1.
По закону полного тока
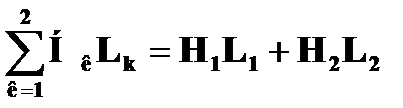 =Um1+Um2=Iω=F,
=Um1+Um2=Iω=F,
где Um1, Um2-магнитные напряжения на различных участках магнитной цепи.
В неразветвленной магнитной цепи магнитный поток одинаков в любом сечении магнитопровода (ток в неразветвленной эл. цепи также одинаков):
Ф=В1 S1=B2S2. (1)
Прямая задача. Пусть задан магнитный поток Ф. Определим МДС F. Из (1) находим В1 и В2.
Н1-находим по рис. В1(Н), а Н2=В2/μo. Тогда МДС определится из выражения:
F=B1 L1/μa+B2 L2/μo=Iω.
Последнее выражение можно записать иначе.
Ф{L1/S1μa+L2/S2μo}=Ф(Rm1+Rm2)=ФΣRmk=Iω=F=Um1+Um2, I=(Eэк-U)/Rэк
Для магнитного зазора Ф=(F-Um1)/Rm2, для ферромагнетика Ф=В1(Н1 ) S1 =Ф(Um1), так как (Н1=Um1/L1)
где Rmk=Lk/Skμk-магнитное (нелинейное) сопротивление к-го участка магнитной цепи.
Тогда для последовательной цепи имеем:
Ф=Iω/Rm аналог (I=U/R)
Последнее выражение по форме напоминает закон Ома для электрической цепи: на месте тока I стоит магнитный поток Ф, на месте напряжения U— намагничивающая сила Iω=HL
Существует формальная аналогия между магнитными цепями с постоянными МДС и электрическими цепями постоянного тока.
Можно нарисовать схему замещения по аналогии с электр. цепью.
| F=Iω |
| Um1 |
| Rm1 |
| Rm2 |
| Um2 |
| Схема замещения |
ΣUm=ΣF
Что аналогично закону Кирхгофа для замкнутого электрического контура
ΣU=ΣЕ.
Аналогично решаются задачи расчета параллельных (разветвленных) магнитных цепей, где в схемах замещения складываются величины, обратные магнитным сопротивлениям, то есть проводимости.
'По аналогии с ВАХ электрических цепей можно построить Вебер-амперную характеристику Ф(Um).
Для нелинейной зависимости магнитной проницаемости ферромагнетика μа(Н) магнитная индукция В(Н) нелинейна, как нелинейно и магнитное сопротивление Rm1.
Магнитное сопротивление зазора линейно, так как магнитная проницаемость зазора не зависит от напряженности Н.
| Н |
| В |
| В |
| μа |
| В1 |
| Н1 |
| Um=HL |
| Ф |
| Um1 |
| Um2 |
| A |
| Ф |
| Ф(Um1) ВАХ |
| Ф=(F-U1m)/Rm2 (Eэк-U)/Rэк |
Аналогом ВАХ является нелинейная зависимость ферромагнетика Ф(Um1 ), аналогом тока I является магнитный поток Ф, аналогом напряжения U есть магнитное напряжение Um, аналогом сопротивления R- магнитное сопротивление Rm
С помощью Вебер-амперной характеристики можно получить решение обратной задачи: по заданной величине МДС F определить требуемый магнитный поток Ф.
Из точки Um=Um1+Um2=F проводим прямую Ф=(F-U1m)/Rm2 для зазора, из начала координат- нелинейную зависимость Ф(Um1) и из условия постоянства магнитного потока по всей магнитной цепи Ф=const в точке пересечения А находим искомый магнитный поток в последовательной цепи
Электромагнитные устройства: трансформаторы
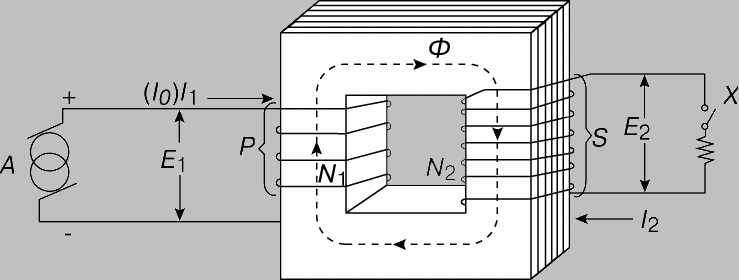
Трансформатор-это устройство для преобразования одного переменного напряжения в другое той же частоты. Он имеет не менее двух обмоток с общим магнитным потоком, которые электрически изолированы друг от друга. Магнитопровод изготовлен из электротехнической стали для усиления индуктивной связи и снижения потерь от вихревых токов (для частот менее 20 кГц).
|
Рис. 1. ТРАНСФОРМАТОР. Схема устройства.
Обозначения на схемах.
| Однофазные трансформаторы |
| Трехфазные трансформаторы |
На щитке трансформатора указываются:
Напряжение низшее (НН)и высшее(ВН).
Номинальная полная мощность (В А или кВ А).
Ток при номинальной полной мощности.
Частота, число фаз, схема соединений и способ охлаждения.
Если первичное напряжение Е1 меньше вторичного -работа в режиме повышающего трансформатора (иначе – понижающего). Можно менять первичную и вторичную обмотки, но в рамках напряжений, указанных на щитке.
Рабочий процесс однофазного трансформатора такой же, как и у одной фазы трехфазного.
Принцип действия.
Ток в первичной обмотке возбуждает в магнитопроводе магнитный поток, который во вторичной обмотке индуцирует ЭДС взаимной индукции Е2. При замыкании вторичной цепи на нагрузку в ней возникает ток I2. Этот ток возбуждает в магнитопроводе встречный потоку от первичной катушки магнитный поток (первичная и вторичная обмотки включены встречно). В итоге суммарная МДС и суммарный магнитный поток в магнитопроводе оказываются пропорциональны I1 N1-I2 N2.
| U1 |
| Rb1 |
| I1 |
| Lpacc/1 |
| U2 |
| I2 |
| Rb2 |
| Lpacc2 |
| Схема замещения трансформатора с активными сопротивлениями Rb и индуктиностями рассеяния обмоток Lpacc |
ЭДС первичной e1=-N1 dФ/dt и вторичной e2=-N2 dФ/dt индуцируются одним и тем же магнитным потоком Ф в магнитопроводе.
Уравнения идеализированного однофазного трансформатора..
У идеализированного трансформатора предполагается линейная зависимость индукции от напряженности магнитного поля B=μr μo H
Тогда по закону электромагнитной индукции в комплексной форме имеем:
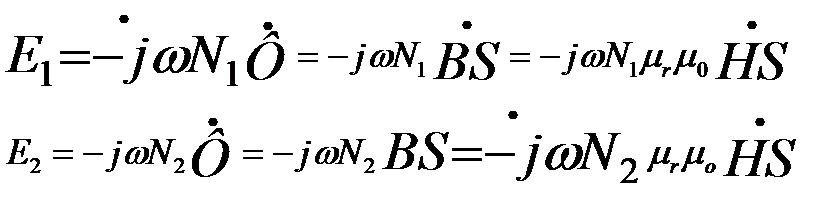
Напряженность на средней линии магнитопровода:
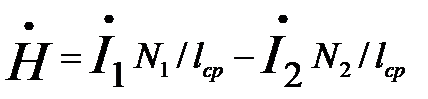
Тогда
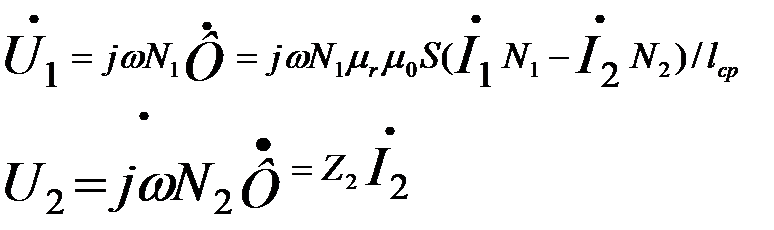
Где Z2-комплексное сопротивление нагрузки.
В режиме холостого хода I2=0
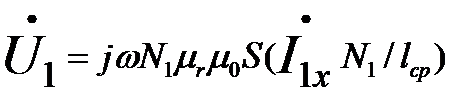 ,где
,где 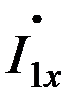 -ток холостого хода или намагничивающий ток.
-ток холостого хода или намагничивающий ток.
Отношение напряжений между вторичной и первичной обмотками пропорционально отношению числа витков в обмотках:
U2/U1=N2/N1=n21-коэффициент трансформации.
| Ф |
| I1x |
| I1 |
| I2 |
| U1 |
| U2 |
| φ1 |
| φ2 |
| δ-угол потерь |
Векторная диаграмма трансформатора.
Режимы работы трансформатора.
1.Номинальный режим -при номинальных значениях тока и напряжения на первичной обмотке I1=I1ном, U1=U1 ном.
2.Рабочий режим U1≈U1 ном, I1 <I1 ном.
3.Режим холостого хода (I2=0).
4. Режим короткого замыкания. U2=0.
Режим холостого хода.
При разрыве внешней цепи на второй обмотке мы имеем индуктивость с магнитопроводом. При измерении вольтметром напряжения на первичной и вторичной обмотках поучаем коэффициент трансформации
n=U2x/U1x, на щитке трансформатора указывают, например, 6000/230 B. Мощность потерь при холостом ходе складывается из мощности потерь в магнитопроводе и мощности потерь в проводах первичной обмотки (Rb1 I21x). Ток холостого хода в первичной обмотке I1x=0.03-0.1 I1n.
Потери энергии на гистерезис и вихревые токи.
При изменении направления напряженности магнитного поля Н в ферромагнетике наблюдается гистерезис. Значение и знак индукции магнитного поля В зависит от величины и направления изменения Н.
Процесс намагничивания ферромагнитных материалов сопровождается изменением и линейных размеров и объёма (магнитострикция).
В переменном магнитном поле внутри проводников возникают вихревые токи Фуко. При этом в середине проводника эти токи
вычитаются из основного тока, а вблизи поверхности –складываются
С увеличением частоты тока f происходит вытеснение тока из середины проводника (скин - эффект). Для снижения потерь на вихревые токи
магнитопровод делают слоистым, перпендикулярным токам.
| Вихревые токи |
| Н |
| гистерезис |
| В |
| Нс |
| -Нс |
| Br |
| -Br |
| <== предыдущая страница | | | следующая страница ==> |
| Символический метод расчета | | | К чему приводит это явление? |
Дата добавления: 2014-08-09; просмотров: 616; Нарушение авторских прав

Мы поможем в написании ваших работ!