
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Числовые характеристики дискретной случайной величины
Дискретные и непрерывные случайные величины. Закон распределения вероятностей дискретной случайной величины.
Лекция 5. Случайные величины.
Определение. Случайной называют величину, которая в результате испытания принимает одно и только одно возможное значение, зависящее от случайных причин.
Определение. Дискретной (непрерывной) называют случайную величину, которая принимает отдельные изолированные возможные значения с определенной вероятностью.
Число возможных значений дискретной случайной величины может быть конечным и бесконечным.
Определение. Непрерывной называют случайную величину, которая может принимать значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно.
Для задания дискретной случайной величины на первый взгляд достаточно перечислить все ее возможные значения.
Законом распределения дискретной случайной величины называют перечень ее возможных значений и их вероятностей. Закон распределения можно задать таблично, аналитически и графически. Случайные величины помимо законов распределения могут описываться числовыми характеристиками.
Среди численных характеристик различают характеристики положения (математическое ожидание, мода, медиана и др.) и характеристики рассеивания (дисперсия, среднеквадратичное отклонение).
Математическим ожиданием (средним значением по распределению) называют число 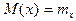 , определяемое формулой:
, определяемое формулой:
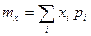 , (5.1)
, (5.1)
где 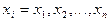 – возможные значения случайной величины;
– возможные значения случайной величины;
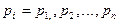 – их вероятности. Причем
– их вероятности. Причем 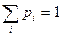 .
.
Мат. ожидание существует, если ряд (5.1.) сходится абсолютно.
Дисперсией случайной величины X называется неотрицательное число 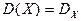 , определяемое формулой:
, определяемое формулой:
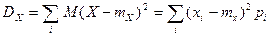 (5.2.)
(5.2.)
Дисперсия существует, если ряд в правой части (5.2.) сходится.
Неотрицльное число 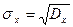 называется среднеквадратичным отклонением случайной величины. Оно имеет размерность случайной величины X и определяет некоторый стандартный среднеквадратичный интервал рассеяния симметрий относительно мат. ожидания.
называется среднеквадратичным отклонением случайной величины. Оно имеет размерность случайной величины X и определяет некоторый стандартный среднеквадратичный интервал рассеяния симметрий относительно мат. ожидания.
(Случайную величину 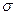 иногда называют стандартным отклонением.) Если случайная величина X постоянна (т.е. X– неслучайна), то дисперсия
иногда называют стандартным отклонением.) Если случайная величина X постоянна (т.е. X– неслучайна), то дисперсия 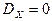 .
.
Случайная величина X называется стандартизованной, если 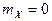 и
и 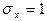 .
.
Случайная величина X называется центрированной, если мат. ожидание 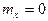 .
.
Начальным моментом k-го порядка распределения случайной величины X (если он существует) называется число 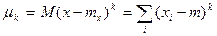 .
.
Из определения моментов в частности следует, что:
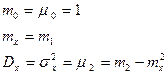
Отметим две важные характеристики распределения, связанные с моментом высшего порядка:
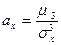 – асимметрия или скошенность распределения,
– асимметрия или скошенность распределения,
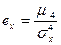 – коэффициент эксцесса или островершинности распределения.
– коэффициент эксцесса или островершинности распределения.
Мода дискретной случайной величины определяется как такое значение случайной величины 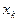 , для которой
, для которой 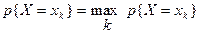 .
.
Мода дискретной случайной величины– ее наиболее вероятное значение (в случае, если такое значение есть). Мода может не существовать, может иметь единственное и множество значений.
Медианой дискретной случайной величины называется такое ее возможное значение, котороеделит распределение на две равные части.
Если число случайных величин нечетно, т.е. 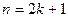 , то медиана
, то медиана 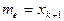 .
.
Если число случайных величин четно, т.е. 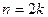 , то медиана
, то медиана 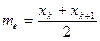 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Постоянной вероятности | | | Статистика |
Дата добавления: 2014-02-26; просмотров: 973; Нарушение авторских прав

Мы поможем в написании ваших работ!