Тема 7. ЭФФЕКТИВНОСТЬ ФИНАНСОВЫХ ОПЕРАЦИЙ

Решение проблемы измерения и сравнения степени доходности финансово-кредитных операций заключается в разработке методик расчета условной годовой ставки для каждого вида операций с учетом особенностей соответствующих контрактов и условий их выполнения.

Расчетная процентная ставка, отражающая общую доходность финансовой операции, имеет различные названия. В простых депозитных и ссудных операциях она называется эффективной, в расчетах по оценке облигаций ее часто называют полной доходностью, в анализе производственных инвестиций для аналогичного по содержанию показателя применяется термин – внутренняя норма доходности. В целом для всех случаев, кроме анализа производственных инвестиций, эта годовая ставка называется – полной доходностью.

Минимальная полная доходность – это расчетная ставка процента, при которой капитализация всех видов доходов от операции равна сумме инвестиций и, следовательно, капиталовложения окупаются. Чем выше полная доходность, тем больше эффективность операции.

Ссудные операции.Доходность этих операций измеряется с помощью эквивалентной годовой ставки сложных процентов.

Условные обозначения:

D – размер ссуды;

n – срок ссуды, выраженный в годах;

G – сумма удержанных комиссионных;

i_э – ставка полной доходности;

D – G – размер фактически выданной суммы.

Наращение величины D – G по ставке полной доходности i_э должно дать тот же результат, что и наращение D по ставке простых процентов – i, т.е.

.

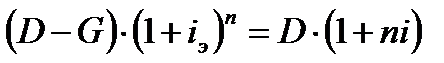Так как сумма удержанных комиссионных G определяется в процентах от номинальной стоимости кредита D, то G=Dq, где q – доля комиссионных в сумме кредита, тогда:

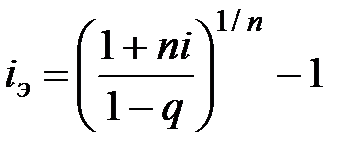. (7.1)

Если полная доходность финансовой операции измеряется в виде ставки простых процентов, получим:

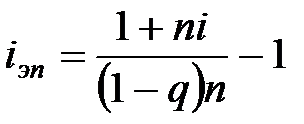. (7.2)

Когда ссуда выдается под сложные проценты i, то исходное уравнение для определения сложной процентной ставки полной доходности i_э, имеет вид:

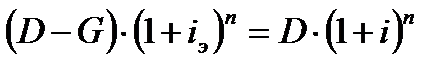, откуда

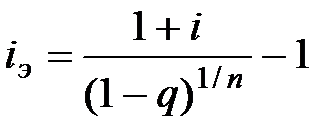. (7.3)

Пример 7.1 При выдаче ссуды на 200 дней под 12 % годовых кредитором удержаны комиссионные в размере 0,8 % от суммы кредита. Какова эффективность ссудной операции в виде годовой ставки сложных процентов, если кредит выдан:

а) по простым процентам; б) по сложным процентам.

Решение. По условию задачи: n = 200/365; i = 0,12; q = 0,008.

Используя формулы (7.1) и (7.2), получим:

а) 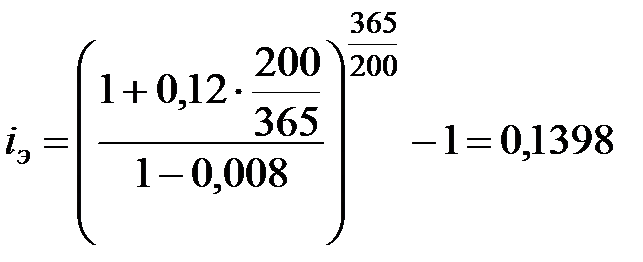или 13,98%;

б) 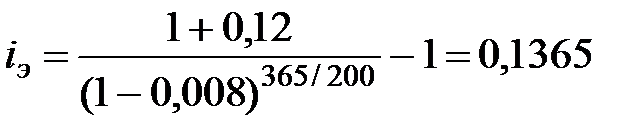или 13,65%.

Учетные операции. При определении ставки доходности операции в виде годовой ставки сложных процентов i_э, если доход извлекается из операции учета по простой учетной ставке d, с удержанием комиссионных и дисконта, то заемщик получит сумму D (1 – n'd – q) или D – Dn^' d – Dq.

D – номинальная стоимость векселя;

Dn'd - дисконт;

G = Dq – сумма комиссионных удержаний;

d – простая учетная ставка;

n^/ - временной интервал между датой учета и датой погашения векселя.

Тогда D (1 – n'd – q ) (1 + i_э)ⁿ = D, отсюда:

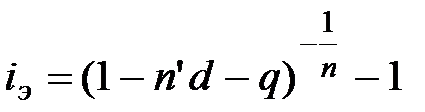. (7.4)

Если эффективность измеряется в виде ставки простых процентов – i_эп., то

D (1 – n'd – q ) (1 + ni_эп) = D, отсюда

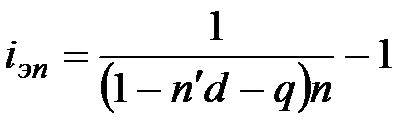. (7.5)

Пример 7.2 Вексель учтен в банке по учетной ставке 8 % годовых за 90 дней до даты погашения. При учете с владельца векселя удержаны комиссионные в размере 0,4 % (К=360 дней). Определить полную доходность операции по ставке сложных процентов.

Решение. По условию задачи 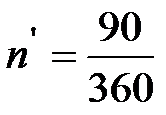, d = 0,08; q = 0,004.

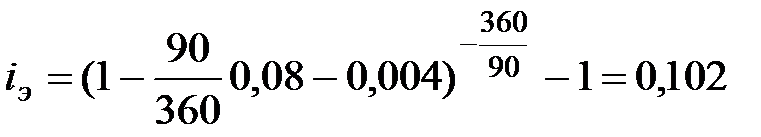или 10,2%.

Покупка и продажа векселя (простая учетная ставка).

Если вексель или другое долговое обязательство через некоторое время после его покупки и до наступления срока погашения продан, то эффективность этой операции можно измерить с помощью ставок простых и сложных процентов.

Финансовая результативность операции здесь связана с разностью цен купли-продажи, которые в свою очередь определяются сроками этих активов до погашения векселя и уровнем учетных ставок.

Обозначим:

S – номинал векселя;

К = 365 дней; К^' = 360 дней;

d₁ – учетная ставка, по которой вексель был куплен;

t₁ – число дней до наступления срока погашения векселя;

t₂ – число дней, до продажи векселя;

d₂ – учетная ставка, по которой вексель был продан;

P₁ – цена векселя в момент его покупки (учета);

P₂ – цена продажи векселя;

t₁ – t₂ – время между моментом покупки и продажи векселя.

Доходность купли продажи (в виде ставки простых процентов i_эп).

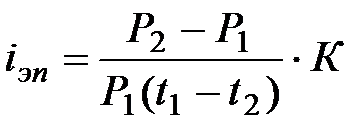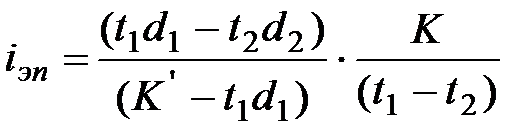или (7.6)

При использовании годовой сложной процентной ставки доходность сделки составит:

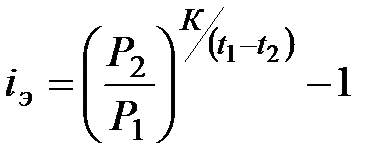или 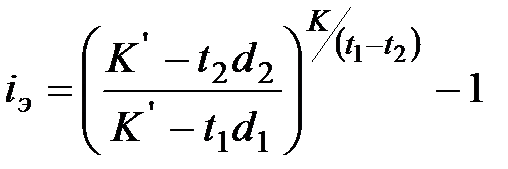. (7.7)

Пример 7.3 Вексель номинальной стоимостью 1 млн. руб. был учтен в банке за 120 дней до его погашения по учетной ставке 9%. Через 30 дней он был переучтен в другом банке по учетной ставке 8%. Определить эффективность данной операции в виде простой и сложной ставки.

Решение. По условию: S = 1 млн. руб., t₁ = 120 дней; t₂ = 120-30 = 90 дней;

d₁ = 0,09; d₂ = 0,08.

Найдем эффективность сделки по формуле (7.6):

.

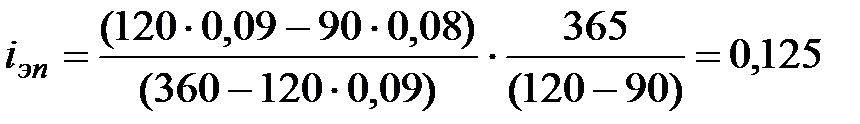Эффективность операции составляет 12,5%.

Если использовать ставку сложных процентов, то эффективность сделки определяется по формуле (7.7):

.

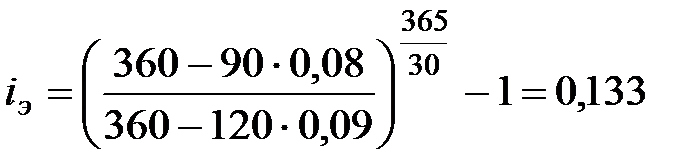Эффективность операции составляет 13,3%.

Операции с депозитными сертификатами.

Если депозитный сертификат, или другой подобного рода краткосрочный инструмент, через некоторое время после его покупки и до наступления срока погашения вновь продан, то доходность такой операции можно измерить в виде ставки простых или сложных процентов.

Если сертификат с разовым начислением процентов, со сроком погашения t₁, покупается по номиналу, продается за t₂ дней до погашения, а процентная ставка сертификата изменилась с i₁ до i₂, то эффективность по простой ставке находится по формуле:

, где К = 365 или 360 дней. (7.8)

Если мерой эффективности служит сложная процентная ставка, то:

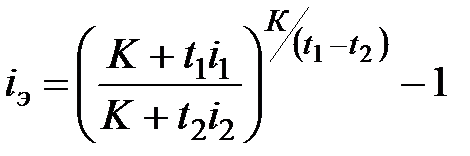. (7.9)

Сертификат покупается после выпуска и погашается в конце срока:

P₁ – номинал финансового инструмента;

P₂ – цена приобретения финансового инструмента;

i – объявленная эмитентом процентная ставка.

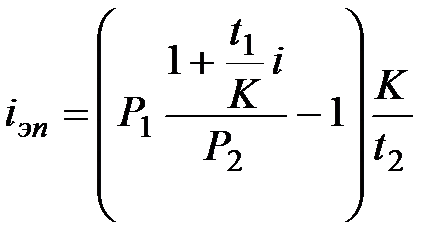; (7.10)

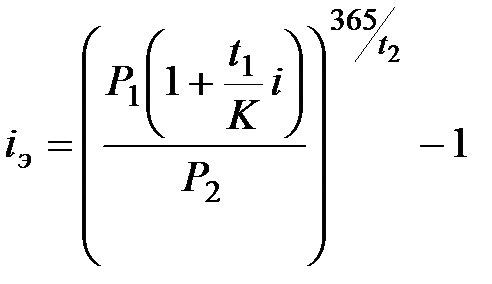. (7.11)

Пример 7.4 Финансовый инструмент, приносящий постоянный процент, куплен за 185 дней до срока его погашения и продан через 120 дней. В момент покупки процентная ставка на рынке была 15,0 %, в момент продажи – 12,7 %. Определить доходность операции купли – продажи в виде годовой ставки сложных процентов.

Решение. По условию t₁ = 185 дней, t₂ = 120 дней, i₁ = 0,15; i₂ = 0,127. Используем формулу (7.9)

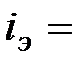
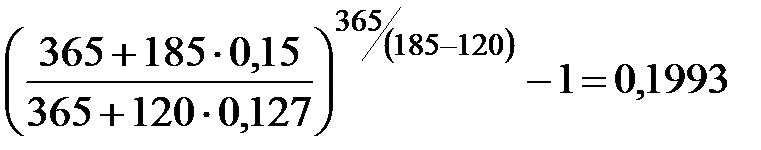или 19,93%.

Задачи для самостоятельного решения

7.1 Банк предоставил кредит в сумме 200 тыс. руб. на 250 дней под 18,0 % годовых простых процентов. При выдаче кредита удержаны комиссионные в размере 0,8 % от величины кредита. Определите годовую ставку полной доходности простых и сложных процентов.

7.2 Банком предоставлен кредит на 300 дней под 12,0 % годовых в сумме 180 тыс. рублей. При выдаче кредита были удержаны комиссионные в сумме 0,5 %. Определите годовую ставку полной доходности сложных процентов, если проценты начислялись: а) по простым процентам; б) по сложным процентам.

7.3 Банком предоставлен кредит сроком на 5 лет в сумме 245 тыс. рублей, под 11,8 % годовых (проценты сложные). При выдаче кредита были удержаны комиссионные в размере 0,7% от величины кредита. Определите годовую ставку полной доходности операции по сложным процентам. На какую величину повысилась стоимость кредита для заемщика вследствие удержания комиссионных?

7.4 Вексель учтен в банке по учетной ставке 12,0 % годовых за 130 дней до его оплаты. При учете векселя удержаны комиссионные в размере 0,4 %. Определите доходность операции в виде простых и сложных процентов.

7.5 Вексель куплен за 158 дней до его погашения с учетной ставкой 8,0 % годовых. Через 67 дней его реализовали по учетной ставке 7,3 %. Определите эффективность операции в виде простой и сложной ставки.

7.6 Вексель стоимостью 140 тыс. рублей учтен банком по учетной ставке 18,0 % годовых за 140 дней до оплаты. Через 60 дней банк переучел его в другом банке по учетной ставке 14,7 % годовых. Определите эффективность данной финансовой операции для банка по простой и сложной ставке. Как изменится эффективность операции, если переучет векселя проведен по учетной ставке 19,8 % годовых?

7.7 Банком выпущен депозитный сертификат номинальной стоимостью 400 тыс. рублей сроком на 11 месяцев по ставке 17,0 % годовых. Определите эффективность следующих финансовых операций:

- клиент приобрел сертификат по номиналу в момент его выпуска и продал его через 90 дней после приобретения по ставке 14,0 % годовых;

- клиент приобрел сертификат через 45 дней после его выпуска и погасил его в конце установленного срока;

- клиент приобрел сертификат через 50 дней после выпуска под 17,0 % годовых, а через 180 дней после приобретения реализовал его по ставке 15,8 % годовых.

7.8 Сертификат с номиналом 140 тыс. рублей, с объявленной доходностью 12,7 % (простые проценты) сроком 640 дней куплен за 165 тыс. рублей за 190 дней до его оплаты. Какова доходность инвестиции?

7.9 Денежный сертификат был приобретен за 170 дней до срока погашения в сумме 90 тыс. рублей и продан за 115 тыс. рублей через 90 дней. Определите доходность операции, если применялась простая и сложная ставка процентов.

7.10 Финансовый инструмент, приносящий постоянный процент, куплен за 250 дней до срока его погашения и продан через 140 дней. В момент покупки процентная ставка на рынке была равна 14,7 %, в момент продажи – 12,5 %. Определите доходность операции купли – продажи в виде годовой ставки сложных процентов.

Вопросы для самоконтроля

1. Что понимается под полной доходностью финансовой операции?

2. Как определяется годовая ставка полной доходности в виде ставки простых и сложных процентов?

3. Из какого уравнения выводится показатель доходности учетных операций?

4. Как определяется доходность операций с векселями?

5. Как оценивается доходность перепродажи депозитного сертификата?

Рекомендуемая литература

Основная учебная литература:

1. Мелкумов Я.С. Финансовые вычисления. Теория и практика, 2-е изд. – М.: ИНФРА – М, 2010. – 416 с.

2. Самаров К.Л. Финансовая математика. Сборник задач с решениями. - М.: Альфа-М, Инфра-М, 2011. - 80 с.

3. Четыркин Е.М. Финансовая математика: – М.: Издательский дом "Дело" РАНХиГС, 2011. – 392 с.

Дополнительная учебная литература:

4. Брусов П.Н., Брусов П.П., Орехова Н.П., Скородулина С.В. Финансовая математика. - М.: КноРус, 2010. - 224 с.

5. Бухвалов А. В., Бухвалова В. В.Финансовые вычисления для менеджеров: учебник., 3-е издание - СПб: Высшая школа менеджмента, 2010. - 368 с.

6. Капитоненко В.В. Задачи и тесты по финансовой математике. - 2-е изд., перераб. и доп. М.: Финансы и статистика, 2011. − 368 с.: ил.

7. Ковалев В.В. Курс финансовых вычислений. М.: Финансы и статистика, 2005. − 559 с.: ил.

8. Статистика финансов: Учебник / Под ред. проф. В.Н. Салина. – М.: Финансы и статистика, 2004. – 816с.: ил.

9. Ширяев В.И. Финансовая математика. Потоки платежей, производные финансовые инструменты: - М.: Либроком, 2009. - 232 с.

Дата добавления: 2014-09-08; просмотров: 1266; Нарушение авторских прав

Мы поможем в написании ваших работ!