
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ОБЩИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
ТЯГОВЫЕ РАСЧЕТЫ
Рекомендовано редакционно-издательским советом университета в качестве методических указаний
для студентов III курса специальности
190300 «Подвижной состав железных дорог»
МОСКВА - 2014
УДК 629.424
Р-83
Руднев В.С. Тяговые расчеты: Методические указания. – М.: МИИТ, 2014. – 48 с.
Приведены методические и справочные материалы, позволяющие студентам самостоятельно выполнять тяговые расчеты для решения отдельных задач магистральных железных дорог.
Ил. 7, табл. 6, библиогр.: 3 назв.
ã МИИТ, 2014
СОДЕРЖАНИЕ
Стр.
ОБЩИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ…………………................4
ЗАДАНИЕ 1. АНАЛИЗ И ПОДГОТОВКА ПРОДОЛЬНОГО ПРОФИЛЯ ПУТИ ДЛЯ ВЫПОЛНЕНИЯ ТЯГОВЫХ РАСЧЕТОВ……………………………………………………… 5
ЗАДАНИЕ 2. РАСЧЕТ ВЕСА (МАССЫ) ГРУЗОВОГО СОСТАВА ПОЕЗДА С УЧЕТОМ ОГРАНИЧЕНИЙ ПО УСЛОВИЯМ ЭКСПЛУАТАЦИИ……………………………...14
ЗАДАНИЕ 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ ДВИЖЕНИЯ ПОЕЗДА ПО УЧАСТКУ МЕТОДОМ А.И. ЛИПЕЦА……….24
ЗАДАНИЕ 4. ОПРЕДЕЛЕНИЕ ВРЕМЕНИ ХОДА ПОЕЗДА ПО УЧАСТКУ МЕТОДОМ Г.В. ЛЕБЕДЕВА…………………34
ЛИТЕРАТУРА………………………………………………… 39
ПРИЛОЖЕНИЕ………………………………………………….40
ОБЩИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
Всем студентам, изучающим теорию тяги поездов, предлагается выполнить четыре индивидуальных задания по тяговым расчетам. Варианты заданий задаются преподавателями кафедры "Локомотивы и локомотивное хозяйство".
Основная цель индивидуальных заданий – привить студентам практические навыки в решении важных задач работы железнодорожного транспорта.
Оформление заданий. При выполнении и оформлении индивидуальных заданий необходимо придерживаться следующих положений:
1. Расчетная часть заданий оформляется на стандартных листах формата А4 (размером 210 х 297 мм) с оставлением полей, мм: левое – 30, правое – 15, верхнее – 20, нижнее - 20. Расчетная часть должна быть представлена в печатном виде с использованием одного из текстовых редакторов.
2. В расчетной части заданий должны быть без сокращения слов кратко изложены необходимые материалы по каждому пункту задания. Текст рекомендуется печатать через 1,5 интервала, размер шрифта – 14.
3. Расчетные формулы набираются в редакторе формул. Сначала формула приводится в общем (аналитическом) виде. Далее поясняются значения величин, входящих в формулу, а затем подставляются числовые величины и записывается результат с указанием единиц измерения. Все формулы должны иметь сквозную нумерацию.
4. Графические построения выполняются на миллиметровой бумаге формата А4 светлых тонов остро заточенным простым карандашом. На осях координат проставляются буквенные обозначения и единицы измерения соответствующих величин.
Точность тяговых расчетов. В расчетах нужно принимать значения основных физических параметров в следующих единицах измерения и с точностью, рекомендованной "Правилами тяговых расчетов для поездной работы":
- крутизну уклона профиля пути - в промилле (%0) с одним знаком после запятой;
- силу тяги - в ньютонах (Н) с округлением до 500Н;
- удельные силы - в Н/кН с двумя знаками после запятой;
- вес состава грузового поезда - в кН с округлением до 500 кН;
- скорость поезда - в км/ч с одним знаком после запятой;
- время хода поезда - в минутах с одним знаком после запятой.
ЗАДАНИЕ 1. АНАЛИЗ И ПОДГОТОВКА ПРОДОЛЬНОГО ПРОФИЛЯ ПУТИ ДЛЯ ВЫПОЛНЕНИЯ ТЯГОВЫХ РАСЧЕТОВ
1. ОБЩИЕ ПОЛОЖЕНИЯ
Основным документом каждой железнодорожной линии является продольный профиль пути, содержащий данные о расположении ее на местности: план линии, отметки высот точек перелома профиля над уровнем моря, крутизна и длина уклонов, расположение кривых, их радиусы, длины, расположение станций (или остановочных пунктов), переездов, искусственных сооружений. Продольные профили могут быть подробными и сокращенными - разница состоит в масштабах изображения. Подробный профиль железных дорог обычно вычерчивают в масштабе 100 мм/км, сокращенный - 20 мм/км. На рис. 1 приведена часть сокращенного профиля железнодорожной линии.
При неизменном режиме работы локомотива и постоянном весе поезда его скорость может изменяться на каждом элементе профиля в зависимости от характера уклона и величины сопротивления движению поезда. В этой связи тяговые расчеты производят для каждого элемента профиля пути в отдельности. Для сокращения объема вычислений действительный продольный профиль пути обычно подвергают предварительной подготовке, состоящей из трех операций:
- анализу профиля пути заданного участка и выбору расчетного подъема;
-группировке небольших по длине элементов и эквивалентной замене каждой группы элементов профиля одним суммарным (при соблюдении правил спрямления);
- замене всех без исключения кривых участков пути "фиктивными" подъемами.
2. ВЫБОР РАСЧЕТНОГО ПОДЪЕМА
Расчетный подъем - это наиболее трудный для движения элемент заданного вариантом профиля пути (приложение 1), на котором, как правило, достигается расчетная (равномерная) скорость движения локомотива с составом.
Расчетным принимается один из самых крутых элементов профиля, имеющий часто наибольшую длину. Данный подъем не может быть пройденным за счет использования кинетической энергии, накопленной поездом на предыдущих элементах профиля без снижения скорости до уровня расчетной.
Пример 1. Дан профиль пути. Установить расчетный подъем* на участке А - В.
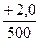
| 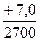
| 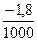
| 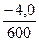
| 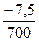
| 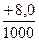
| ||||
| Ст. А | Sкр= R=1400 | Sкр= R= | Sкр= R= | Ст. В |
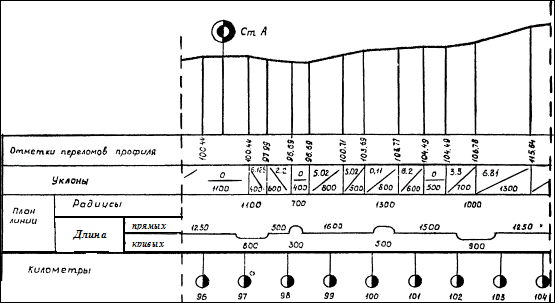
Рис. 1. Сокращенный продольный профиль железнодорожного пути (часть)
* Правилами тяговых расчетов установлены следующие обозначения уклонов: подъем - "+", спуск - "-", площадка - "0"; в числителе указывается величина уклона в тысячных долях числа, в знаменателе – длина элемента профиля в метрах.
В качестве расчетного подъема в данном случае нужно принять элемент +7/2700, так как он является самым трудным для преодоления . Поезд тронулся со Ст. А. и сразу начался подъем небольшой (500 м) длины, следовательно, перед следующим подъемом, который принят в качестве расчетного, скорость поезда будет невелика, вследствие чего кинетическая энергия поезда будет недостаточной для преодоления достаточного затяжного (2700м) подъема "по инерции".
В свою очередь, элемент профиля +8/1000 хотя и является самым крутым на участке А-В, но лежащие перед ним элементы профиля дают возможность машинисту разогнать поезд и использовать для преодоления данного подъема кинетическую энергию, накопленную поездом. Поэтому подъем +7%о на участке А-В является наиболее трудным для преодоления (для доказательства нужна дополнительная проверка). Наличие на элементе +7/2700 кривой делают его еще более трудным для преодоления.
В ряде вариантов анализ профиля пути не позволяет дать столь однозначные ответы, так как два и более элементов одного направления могут быть примерно одинаковыми по трудности преодоления. В данном случае нужно сделать следующее. За расчетный может быть принят ориентировочно наименее крутой из сравниваемых подъемов. Остальные (более крутые) подъемы условно можно назвать "проверяемые подъемы" и не группировать их с другими элементами профиля при спрямлении. Правильность выбора расчетного подъема может быть установлена лишь при выполнении задания 2.
3. ПОДГОТОВКА ПРОФИЛЯ ПУТИ ДЛЯ ВЫПОЛНЕНИЯ РАСЧЕТОВ
При выполнении тяговых расчетов, связанных с движением поезда, число элементов действительного (заданного) продольного профиля пути уменьшают за счет группировки небольших по длине элементов и эквивалентной замене каждой группы элементов профиля одним суммарным. Одновременно все кривые, находящиеся на пути, спрямляют в плане, заменяя их фиктивными подъемами.
Помимо сокращения объема вычислений предварительная подготовка профиля (спрямление) в ряде случаев позволяет уменьшить неизбежные погрешности тяговых расчетов. Представим, при движении грузового поезда его вагоны одновременно могут находиться на нескольких коротких элементах профиля (рис. 2.а). В этом случае нет смысла учитывать самостоятельное влияние сопротивления движению поезда каждого из этих элементов, а целесообразно объединить их в один суммарный (рис. 2.б).
Крутизна уклона суммарного профиля i’c представляет собой отношение разности отметок высот (Нк – Нн) крайних точек к его длине Sс (см. рис. 2), увеличенное в 1000 раз, %0:
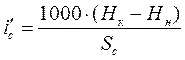 , (1)
, (1)
где Нк – Нн - разность отметок высоты головки рельса в конце и начале суммарного участка над уровнем моря, м;
Sс – суммарная длина спрямляемых элементов профиля, м;
%о - промилле (тысячная часть числа), т. е. 1 %о = 0,001.
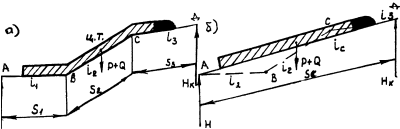
Рис. 2. Замена группы элементов (а) одним спрямленным (б).
При отсутствии отметок высот крутизна суммарного профиля определяется по следующей формуле, %о:
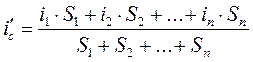 , (2)
, (2)
где 1, 2, … n – номера спрямляемых элементов.
Для избежания больших погрешностей при тяговых расчетах, например, при определении времени хода поезда по участку, необходимо провести проверку допустимости замены группы элементов действительного профиля одним суммарным. Данная проверка проводится для каждого (i-ого) в отдельности элемента действительного профиля, входящего в спрямляемый участок по формуле, м:
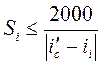 . (3)
. (3)
При анализе профиля пути все кривые участки пути заменяют фиктивными подъемами по формуле, %о:
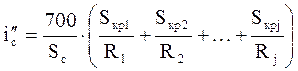 , (4),
, (4),
а при задании их центральными углами a°:
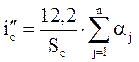 , (5)
, (5)
где 1, 2, … n – номера кривых участков пути, находящихся на спрямляемом участке;
Sкр – длина кривой в пределах спрямленного участка, м;
R – радиус кривой, м;
a - центральный угол кривой радиусом Ri, град.
Окончательная крутизна уклона спрямленного участка с учетом кривых (приведенный уклон), %о
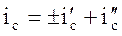 . (6).
. (6).
Знак перед величиной 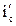 определяется характером уклона спрямленного участка: подъем - "+", спуск - "-".
определяется характером уклона спрямленного участка: подъем - "+", спуск - "-".
Величина фиктивного уклона 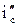 , заменяющего действие дополнительного сопротивления от кривых, всегда положительна.
, заменяющего действие дополнительного сопротивления от кривых, всегда положительна.
Основные правила спрямления:
1. Спрямлению подлежат рядом лежащие элементы профиля, имеющие одинаковый знак и относительно небольшую длину. Площадки (0%о) могут быть спрямлены с уклоном любого знака.
2. Расчетный и проверяемые подъемы, а также раздельные пункты (станции) спрямлению не подлежат.
3. Проверка возможности спрямления производится по (3) для каждого элемента действительного профиля, входящего в спрямляемый участок.
4. Дополнительное сопротивление, возникающее при движении поезда в кривых, учитывается фиктивными подъемами, величина которых определяется по (4).
Пример 2. Подготовить профиль пути, приведенный в примере 1, для выполнения тяговых расчетов.
Решение:
1) анализ профиля пути показывает, что возможна группировка и замена суммарным лишь трех элементов: 0/900; -1,8/1000; -4,0/600; на двух последних из них и на элементе +7/2700 расположены кривые;
2) определим суммарный уклон без учета кривых по (2):
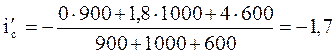 %0
%0
3) проверяем по (3) возможность спрямления для каждого действительного элемента профиля:
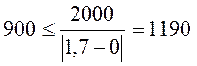 м
м
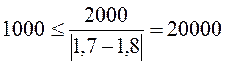 м
м
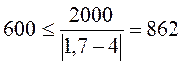 м
м
Во всех трех случаях условия проверки выполняются;
4) определим величину фиктивного подъема от кривых для суммарного участка по (4):
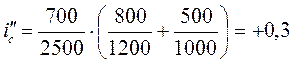 %0;
%0;
5) величина приведенного уклона суммарного участка:
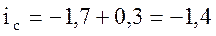 %0
%0
6) аналогично поступаем с кривой на элементе +7/2700:

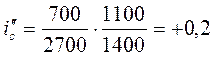 %0
%0
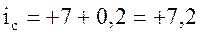 %0
%0
7) результаты расчета заносим в таблицу 1.
Таблица 1
Расчет спрямления профиля
| № п/п | Действительный профиль | Спрямленный профиль | Проверка | |||||
| S, м | I, %0 | R, м | Sкр, м | I, %0 | S, м | № п/п | ||
| Ст. А | ||||||||
| +2,0 | +2,0 | |||||||
| +7,0 | +7,2 | расчетный | ||||||
| -1,4 | 900<1190 | |||||||
| -1,8 | 1000<20000 | |||||||
| -4,0 | 600<862 | |||||||
| -7,5 | -7,5 | |||||||
| +8,0 | +8,0 | проверяемый | ||||||
| Ст. В |
4. ПОРЯДОК ВЫПОЛНЕНИЯ ЗАДАНИЯ
1. В соответствии с заданным преподавателем вариантом направления движения поезда (прил. 1) выбрать расчетный и проверяемые подъемы на продольном профиле пути. Приведенные в приложении 1 профили пути соответствуют движению поезда от ст. А до ст. В (нечетный вариант). При четном варианте поезд движется от ст. В к ст. А; в этом случае приведенные в приложении 1 знаки уклонов следует заменить на обратные, а элементы профиля расположить в таблице в соответствии с нумерацией, приведенной в скобках, т.е. в верхней строке таблицы расположить элемент профиля «ст. В» и т.д., а в нижней – элемент профиля «ст. А».
2.Сгруппировав смежные элементы профиля, подлежащие спрямлению, определить по (2) суммарные уклоны без учета сопротивления от кривых.
3. Используя (4) и (6), определить величины фиктивных подъемов от кривых и приведенных уклонов.
4. Результаты расчетов занести в таблицу, аналогичную табл. 1.
ЗАДАНИЕ 2. ОПРЕДЕЛЕНИЕ ВЕСА (МАССЫ) СОСТАВА ГРУЗОВОГО ПОЕЗДА С УЧЕТОМ ОГРАНИЧЕНИЙ ПО УСЛОВИЯМ ЭКСПЛУАТАЦИИ
1.Определение расчетного веса (массы) состава грузового поезда
Вес состава грузового поезда является одним из важнейших качественных показателей работы железных дорог. Правильный выбор веса состава грузового поезда позволяет снизить себестоимость и повысить экономичность перевозок, наиболее полно использовать мощность локомотивов без снижения надежности их работы в эксплуатации. Превышение весовых норм поездов, в свою очередь, может вызвать порчи локомотивов в пути следования и, соответственно, привести к нарушению графика движения поездов.
В качестве примера: в 2013 году средний вес грузового поезда на сети железных дорог России составил около 40000 кН (4000 т).
Расчетный вес состава грузового поезда Qр определяется исходя из условия полного использования мощности заданной серии локомотива при равномерном движении по расчетному подъему с расчетной скоростью, кН:
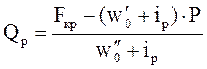 , (7)
, (7)
где Fкр – расчетная сила тяги локомотива (с учетом числа секций) при расчетной скорости vр, Н;
Р – расчетный (сцепной) вес локомотива (с учетом числа секций), кН;
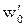 - основное удельное сопротивление движению локомотива в режиме тяги при расчетной скорости, Н/кН;
- основное удельное сопротивление движению локомотива в режиме тяги при расчетной скорости, Н/кН;
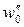 - основное удельное сопротивление движению грузового состава (вагонов) при расчетной скорости, Н/кН;
- основное удельное сопротивление движению грузового состава (вагонов) при расчетной скорости, Н/кН;
iр - крутизна расчетного подъема, %о (из задания 1).
Расчетные значения силы тяги, скорости и веса основных серий локомотивов приведены в таблице 2. Эмпирические формулы для расчета основного удельного сопротивления движению локомотива, вагонов и поезда - в таблице 3. В эмпирических формулах (см. табл. 3) величины a, b, g - задаются преподавателем вариантом согласно приложения 2; q04, q06, q08 – масса, приходящаяся на одну ось вагонов вышеуказанных типов, соответственно, т; определяется делением массы вагона соответствующего типа (заданы приложением 2) на число осей.
Расчетная масса состава грузового поезда, т:
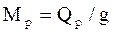 , (8)
, (8)
где g - ускорение свободного падения, м/с (g = 9,81 м/с).
2. Уточнение веса грузового состава с учетом ограничений
Расчетный вес состава грузового поезда, который
Таблица 2
Расчетные параметры грузовых локомотивов.
| Серия | Расчетная скорость Vp, км/ч | Расчетная сила тяги, Fкр х 103, Н | Касательная мощность при Vp, Nк, кВт | Расчетный вес P, кH | Сила тяги при V=0 Fкр × 103, Н | Конструкционная скорость Vk, км/ч | Длина локомотива lл, м |
| ТЭЗ | 20,5 | ||||||
| М62 | 20,0 | ||||||
| 2М62У | 20,0 | ||||||
| 21Э10Л | 23,4 | ||||||
| 2ТЭ10В | 23,4 | ||||||
| ЗТЭ10М | 23,4 | ||||||
| 2ТЭ116 | 24,2 | ||||||
| 2ТЭ121 2ТЭ25К 2ТЭ25А | 26,6 24,0 18,5 | ||||||
| ВЛ23 | 43,3 | ||||||
| ВЛ8 | 43,3 | ||||||
| ВЛ10У | 45,8 | ||||||
| ВЛ11 | 46,7 | ||||||
| ВЛ15 2ЭС10 | 45,0 55,0 | ||||||
| ВЛ60к | 43,5 | ||||||
| ВЛ80с | 43,5 | ||||||
| ВЛ85 2ЭС5К | 50,0 51,0 |
был определен из условия равномерного движения по расчетному подъему с расчетной скоростью, следует уточнить (проверить) по условиям эксплуатации. К числу ограничений веса поезда по условиям эксплуатации можно отнести: длину приемо-отправочных путей станций; возможность трогания поезда с места; перегрев обмоток тяговых электродвигателей локомотивов; прочность автосцепных приборов и ряд других.
Таблица 3
Расчетные формулы для определения основного удельного сопротивления движению подвижного состава на звеньевом пути
| Тип подвижного состава | Расчетная формула (w0 – [Н/кН]; q0 – [т]; v – [км/ч]) |
| Тепловозы и электровозы: | |
| - режим тяги | 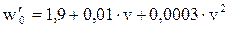
|
| - режим холостого хода | 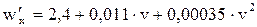
|
| Вагоны груженые: | |
| - четырехосные * | 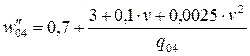
|
| - шестиосные* | 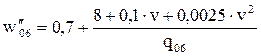
|
| - восьмиосные* | 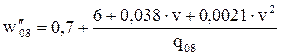
|
| Состав поезда | 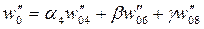
|
*- все типы вагонов оборудованы буксами с роликовыми подшипниками.
Также расчетный вес поезда следует проверить на возможность преодоления более крутых подъемов, чем
расчетный, за счет использования кинетической энергии поезда.
2.1. Проверка на возможность преодоления проверяемых подъемов за счет использования кинетической энергии поезда
Данная проверка проводится в том случае, если затруднен (задание 1) выбор величины расчетного подъема.
Основная задача проверки - сможет ли машинист локомотива провести поезд расчетного веса по самым трудным для преодоления элементам профиля (кроме расчетного подъема) со скоростью в конце подъемов не ниже расчетной, используя кинетическую энергию движущегося поезда.
В общем случае проверка может состоять из двух этапов.
На первом этапе возможность преодоления проверяемых подъемов только за счет использования кинетической энергии поезда устанавливается с помощью номограммы, представленной на рис. 3. При этом считается (условно), что машинист локомотива ведет поезд по проверяемым подъемам в режиме холостого хода.
Порядок пользования номограммой (см. рис. З):
1. Задаемся значением начальной скорости движения поезда по проверяемому подъему, можно принять v = 70 км/ч (точка "А").
2. Из точки "А" восстанавливаем перпендикуляр до пересечения с кривой S = f(v), построенной для крутизны, равной уклону проверяемого элемента. В качестве примера 3 проверим подъем +8/1000 (см. задание 1), поезд ведет электровоз ВЛ15; в результате получаем точку "В".
3. Точку "В" переносим на ось ординат и получаем точку "С". От точки "С" вниз откладываем длину проверяемого участка 1000 м и фиксируем точку "Д" (Sпр).
4. Точку "Д" проектируем вновь на кривую S = f(v), для i = + 8%0 - получаем точку "Е". Затем через точку "Е" проводим перпендикуляр до пересечения с осью абсцисс (точка F) и в результате получаем скорость поезда в конце
проверяемого элемента vк = 58 км/ч. Для электровоза ВЛ15 vр = 45,0 км/ч (см. табл. 2), следовательно, vк > vр.
При выполнении условия vк ³ vр для всех проверяемых подъемов можно сделать вывод, что расчетный подъем выбран правильно и приступить к следующим проверкам или уточнениям величины расчетного веса поезда.
Второй этап проверки проводится в случае невыполнения условия vк ³ vр для одного или нескольких проверяемых подъемов.
При этом учитывается то обстоятельство, что машинист локомотива ведет поезд по подъемам в режиме тяги и на движущийся поезд действуют ускоряюще одновременно сила тяги и ранее накопленная им кинетическая энергия.
Путь S, который может пройти поезд по проверяемому подъему при работе локомотива в режиме тяги, используя ранее накопленную кинетическую энергию при снижении скорости не ниже расчетной, не должен быть меньше длины данного подъема Sпр, т.е. S ³ Sпр.
Расчет длины пути S (м): выполняется для каждого из проверяемых подъемов по формуле:
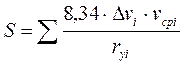 , (9)
, (9)
где n - число i -ых интервалов изменения скорости от начальной vн (можно принять vн = 70 км/ч) до конечной vк (можно принять равной расчетной скорости, т.е. vк = vр) с шагом Dv £ 10 км/ч;
Dvi - заданный интервал (шаг) изменения скорости от начальной vн до конечной vк, т.е. Dvi = vкi – vнi;
Dvср - средняя скорость движения поезда на i -ом интервале ее изменения, т.е. 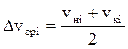 , км/ч;
, км/ч;
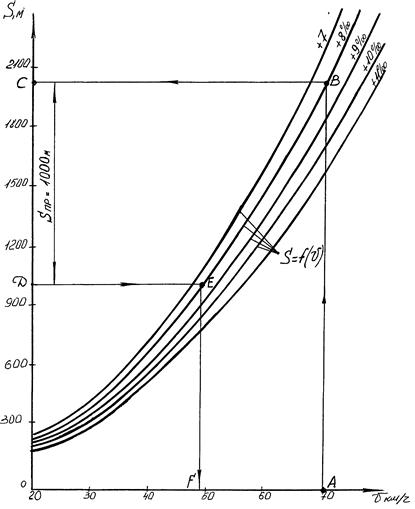
Рис. 3. Определение конечной скорости движения поезда на проверяемом подъеме.
rуi - среднее значение удельной равнодействующей силы, действующей на поезд в каждом интервале скоростей Dvi , Н/кН:
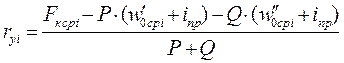 , (10)
, (10)
где iпр - крутизна проверяемого элемента профиля, %о;
Fк срi - сила тяги локомотива [Н], соответствующая средней скорости движения vср в i-ом интервале ее изменения; определяется по внешней тяговой характеристике F=f(v) локомотива, [Н];
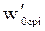 ,
, 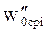 - основное удельное сопротивление движению локомотива и вагонов; определяются по формулам, приведенным в таблице 3, для vср, Н/кН.
- основное удельное сопротивление движению локомотива и вагонов; определяются по формулам, приведенным в таблице 3, для vср, Н/кН.
При невыполнении условия S ³ Sпр на любом из проверяемых элементов профиля за расчетный подъем следует принять крутизну данного проверяемого подъема и вновь по формуле (7) определить величину расчетного веса состава грузового поезда.
Второй этап данной проверки рекомендуется выполнить на ЭВМ.
Алгоритм программы данной проверки веса поезда и пример его реализации на персональном компьютере приведены в приложении 4.
2.2. Уточнение веса поезда в соответствии с числом вагонов
При расчете величины Qр не учитывалось то обстоятельство, что поезд состоит из конкретного числа вагонов различного типа. Поэтому расчетный вес поезда необходимо уточнить в соответствии с реальным числом вагонов (кН):
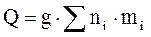 , (11)
, (11)
где mi - масса грузового вагона i-го типа, т (из приложения 2);
ni - число вагонов (целое число) i-го типа в составе поезда
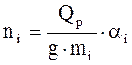 , (12)
, (12)
где ai - доля веса вагонов i-го типа в составе поезда (из приложения 2).
2.3. Проверка по длине приемо-отправочных путей станции.
Длина поезда lп при уточненном весе состава не должна превышать длину приемо-отправочных путей станции (для возможности скрещения, остановки или обгона), т.е. lп £ lст.
Длина поезда с учетом допуска на неточность установки поезда 10 м, (м):
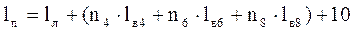 , (13)
, (13)
где lв4, lв6, lв8 - длина четырех-, шести-, восьмиосных вагонов по осям автосцепок, соответственно, м (приведена в табл. 4);
lл - длина локомотива по осям автосцепок, м (см. табл. 2).
При невыполнении условия lп £ lст число вагонов (любого типа) в составе и, следовательно, вес грузового состава должны быть уменьшены. Длину приемо-отправочных путей станции можно принять равной 1250 м.
Таблица 4
Условная длина некоторых типов вагонов
| Тип вагона | Длина вагона, м |
| Четырехосные полувагоны | |
| Шестиосные полувагоны | |
| Восьмиосные полувагоны |
2.4. Определение максимальной крутизны подъема imax, на котором возможно трогание с места поезда уточненного веса Q после остановки
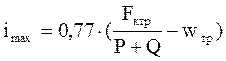 , (14)
, (14)
где Fктр - максимальная сила тяги локомотива при трогании с места, Н (см. табл.2);
wтр - удельное сопротивление состава поезда при трогании с места на прямом горизонтальном пути (Н/кН):
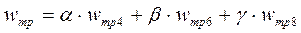 , (15)
, (15)
где wтрi - удельное сопротивление при трогании вагона i-го типа, Н/кН.
Для вагонов i -го типа на подшипниках качения (Н/кН):
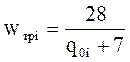 . (16)
. (16)
Для 4-осных вагонов на подшипниках скольжения, Н/кН:
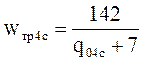 . (17)
. (17)
На элементах профиля с крутизной подъема больше величины imax должно быть предусмотрено только безостановочное движение поездов с установленной весовой нормой Q.
Масса грузового поезда Мп , с учетом ограничений по условиям эксплуатации, т:
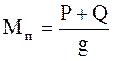 . (18)
. (18)
3. Порядок выполнения задания
1.В соответствии с заданным преподавателем вариантом характеристики состава грузового поезда (см. прил. 2), используя результаты, полученные при выполнения задания 1, определить расчётный вес состава Qр.
2.Используя (9)-(17), проверить соответствие полученного веса грузового состава условиям эксплуатации.
3. По (18) определить массу грузового поезда, округлив ее значение с точностью до 50 т.
4. Результаты расчетов аккуратно оформить в виде задания 2 и представить преподавателю для проверки.
ЗАДАНИЕ 3. РАСЧЕТ СКОРОСТИ ДВИЖЕНИЯ ПОЕЗДА ПО УЧАСТКУ МЕТОДОМ А.И. ЛИПЕЦА
Для определения скорости движения поезда по участку рекомендуется использовать графический способ МПС (метод А. И. Липеца). Результаты расчета представляются студентами в виде кривой v = f(S), выполненной в масштабе на миллиметровой бумаге формата А4.
1. Основные положения метода А.И. Липеца
Движение поезда складывается из трех основных режимов его ведения: тяги, холостого хода и полного служебного торможения. В исключительных случаях машинист имеет возможность также применить режим экстренного торможения.
В практике тяговых расчетов принято использовать т.н. "удельные" силы (отнесенные к единице веса поезда), действующие на поезд при его движении: удельная сила тяги fк, удельное сопротивление wк, удельная тормозная сила bт. Необходимо отметить, что в действительности "удельные" силы fк, wк, bт,, являются безразмерными, т.е. относительными, если силы, действующие на поезд, измерять в "кН". Но, получаемые при этом величины относительных сил, будут составлять сотые и даже тысячные доли числа (например, 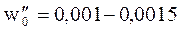 ), что неудобно для расчетов и сравнения величин. Поэтому силы, действующие на поезд, измеряют в "Ньютонах", т.е. увеличивают по величине на 103 и, относя их к весу поезда кН, получают условную единицу измерения удельных сил "Н/кН".
), что неудобно для расчетов и сравнения величин. Поэтому силы, действующие на поезд, измеряют в "Ньютонах", т.е. увеличивают по величине на 103 и, относя их к весу поезда кН, получают условную единицу измерения удельных сил "Н/кН".
В соответствии с уравнением движения поезда равнодействующая удельных сил r в зависимости от режима ведения поезда по прямому горизонтальному пути определяется следующими уравнениями (Н/кН):
режим тяги (ускоряющая сила):
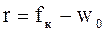 (19)
(19)
режим холостого хода (замедляющая сила):
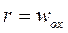 (20)
(20)
режим полного служебного торможения (замедляющая сила):
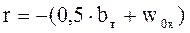 . (21)
. (21)
При движении поезда по уклонам в соответствующем режиме значение удельной равнодействующей силы будет отличаться на величину крутизны
уклона, т.е. rу = ± (r+i), Н/кН.
Рекомендуется обозначать удельные силы, действие которых вызывает ускорение поезда (например, крутизна спуска), знаком "+", замедление - "-".
Метод Липеца А. И. расчета скорости (графическое интегрирование уравнения движения поезда) основан на геометрической связи между кривыми ускоряющих и замедляющих сил и скорости движения поезда v = f(S) при соответствующем подборе масштабов этих величин.
В таблице 5 приведены масштабы величин, которые рекомендуются для практического использования при выполнении задания 3.
Таблица 5
Масштабы для графических построений
| Величина | Единицы измерения | Обозначение масштаба | Для расчета скорости и времени хода поезда, мм |
| Удельные силы | 1 Н/кН | к, мм | |
| Скорость | 1 км/ч | m, мм | |
| Путь | 1 км | y, мм | |
| Время | 1 мин | x, мм | |
| Постоянная | - | D, мм |
Основные допущения метода Липеца А.И.: удельные силы, действующие на поезд при движении по прямому горизонтальному пути в произвольно выбранном интервале изменения скорости (не более 10 км/ч), принимаются постоянными и соответствующими средней скорости на этом интервале; поезд рассматривается как материальная точка, у которой вес сосредоточен в центре ее тяжести (т.е. при построении кривой скорости длина поезда не учитывается).
2. Порядок построения кривой скорости
1. На миллиметровой бумаге с вычерченным спрямленным профилем пути по данным приложения 3 в масштабе строят три графические зависимости, соответствующие режимам движения локомотива: тяги fк – w0 = f(v), холостого хода w0x = f(v) и служебного торможения 0,5bт – w0x = f(v). При этом ось удельных равнодействующих сил (абсцисс) совмещают с осью пути S спрямленного профиля, а ось скорости v (ординат) - с началом рассматриваемого участка пути (ст. А). Слева от оси скорости строят график ускоряющих сил, справа - кривые замедляющих сил. Для разграничения смежных профилей пути проводят вертикальные линии.
2. Задаются интервалом изменения скорости Dv = vк – vн при условии Dv £ 10 км/ч. Определяют среднее значение скорости, км/ч на выбранном интервале ее изменения vср = (vк + vн)/2.
3. В зависимости от скорости движения и перспективы изменения дополнительного сопротивления движению поезда от уклона выбирают один из режимов ведения поезда: тяги (РТ), холостого хода (XX) или полного служебного торможения (ТР), при этом необходимо стремиться к тому, чтобы, с одной стороны, поезд развивал на каждом элементе наибольшую допустимую скорость движения, а с другой - к экономии энергоресурсов на тягу поезда.
4. По кривым равнодействующих сил на общем планшете (лист миллиметровой бумаги с ранее выполненными построениями профиля пути) строят кривую скорости v = f(S).
В качестве примеров на рис. 4 и 5 показана методика построения кривой скорости с использованием всех режимов ведения поезда.
Движение поезда начинается в начале координат – т. 0 (см. рис.4) и заканчивается в конце станции В - т. 01 (см. рис. 5). В соответствии с выбранным режимом движения по средней скорости принятого интервала ее изменения на одной из кривых находят значение равнодействующей силы (см. рис.4 и 5, т. a1, a2, ...), действующей на поезд на прямом горизонтальном пути. По профилю определяется величина и знак уклона элемента, на котором предполагается дальнейшее движение поезда.
Учитывая, что одна тысячная (промилле) уклона дополнительно действует с силой в 1 Н на каждый килоньютон веса поезда, т.е. 1 %о = 1 Н/кН, ось уклонов совмещают с осью удельных сил, откладывая в масштабе влево от начала координат (т. 0) подъемы, вправо - спуски. Через точки, соответствующие значению r = f(v) в интервале изменения скорости Dv (a1, a2, ...) и величине уклона элемента, по которому двигается поезд, на оси уклонов, проводится прямая (a1b1, a2b2, ...), к которой из начала координат (vн) восстанавливается перпендикуляр до пересечения с проекцией конечной скорости vк выбранного интервала ее изменения Dv. Полученный отрезок, который определяет характер изменения скорости в интервале Dv, и является элементом зависимости v = f(S).
Дальнейшее построение кривой скорости ведут аналогичным образом, только за начальную скорость движения поезда на следующем интервале ее изменения принимают конечную на предыдущем, т.е. 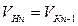 , и, соответственно, перпендикуляр восстанавливается из точки, соответствующей
, и, соответственно, перпендикуляр восстанавливается из точки, соответствующей 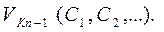
Так, в примере, рассмотренном на рис. 4, в качестве первого интервала изменения скорости выбрано DV1 = Vk1 – Vн1 = 10 – 0 = 10 км/ч, средняя скорость для DV1 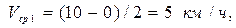 режим движения – РТ.Покривой
режим движения – РТ.Покривой 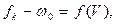 соответствующей режиму тяги, определяем значение равнодействующей (ускоряющей) силы поезда Н/кН - т.а1. Так как движение поезда начинается на площадке (первый элемент), через т. а1. и т. 0 проводим прямую а1b1, к которой затем из начала координат
соответствующей режиму тяги, определяем значение равнодействующей (ускоряющей) силы поезда Н/кН - т.а1. Так как движение поезда начинается на площадке (первый элемент), через т. а1. и т. 0 проводим прямую а1b1, к которой затем из начала координат 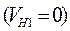 восстанавливаем перпендикуляр ос1 до проекции скорости Vk1
восстанавливаем перпендикуляр ос1 до проекции скорости Vk1 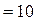 км/ч (т. C1). Второй интервал
км/ч (т. C1). Второй интервал 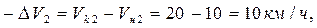
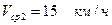
 Находим т. а2, проводим а2 b2, а затем уже из т. с1 к прямой а2 b2 восстанавливаем перпендикуляр с1с2 до
Находим т. а2, проводим а2 b2, а затем уже из т. с1 к прямой а2 b2 восстанавливаем перпендикуляр с1с2 до 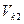
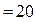 км/ч (т. с2).
км/ч (т. с2).
Отметим ряд особенностей, с которыми приходится встречаться при построении кривой скорости методом Липеца А.И.:при движении поезда на спусках его максимальная скорость не должна превышать допустимую (по ПТР) скорость движения грузовых поездов 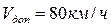 . Следовательно, при
. Следовательно, при 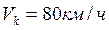 необходимо применять тормозной режим (см. рис. 5, прямая
необходимо применять тормозной режим (см. рис. 5, прямая
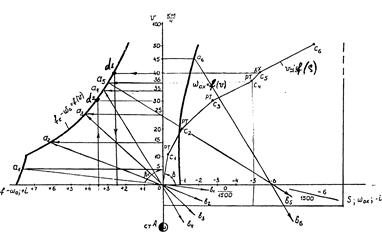
Рис. 4. Построение кривой скорости v (S) в режимах тяги и холостого хода. 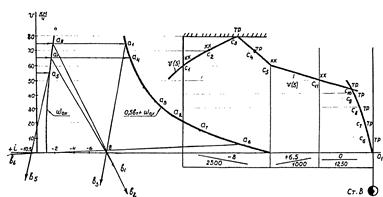
Рис. 5. Построение кривой скорости v (S) в режимах холостого хода и служебного торможения
с3с4);для максимального использования кинетической энергии поезда скорость к началу подъема должна быть наибольшей;для остановки поезда в конце ст. В (см. рис. 5) применяют режим полного служебного торможения. Кривую скорости при этом режиме движения строят из т. О, начиная с интервала 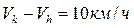 , до пересечения с ранее построенной кривой скорости (т. с10).
, до пересечения с ранее построенной кривой скорости (т. с10).
При проходе входных стрелок ст. В (начало последнего элемента профиля) скорость движения не должна превышать величины 40 км/ч; при выборе интервала изменения скорости в конце элемента профиля, значение конечной скорости должно совпадать с линией, разграничивающей смежные профили;на точность графического расчета скорости движения поезда по участку влияет не только правильность выбора интервала изменения скорости из условия 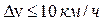 , но и определение характера изменения скорости (возрастет, будет падать, станет постоянной), особенно при переходе с элемента на элемент. Для определения характера изменения скорости необходимо определить знак удельной равнодействующей силы
, но и определение характера изменения скорости (возрастет, будет падать, станет постоянной), особенно при переходе с элемента на элемент. Для определения характера изменения скорости необходимо определить знак удельной равнодействующей силы 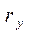 , действующей на поезд, при заданном режиме ведения поезда и при условии движения по элементу известной крутизны с постоянной скоростью (H/кН)
, действующей на поезд, при заданном режиме ведения поезда и при условии движения по элементу известной крутизны с постоянной скоростью (H/кН)
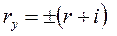 , (22)
, (22)
где r - равнодействующая удельных сил при движении поезда по прямому горизонтальному пути, Н/кН;определяется по графикам 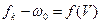 ;
; 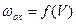 и
и
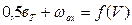 для значения скорости, с которой поезд начинает движение по следующему элементу профиля пути.
для значения скорости, с которой поезд начинает движение по следующему элементу профиля пути.
Покажем это на примере 4.Допустим поезд начинает движение по элементу +3,5/2000 со скоростью 40 км/ч в режиме тяги (см. рис. 4). Выбираем следующий шаг изменения скорости DV= 10 км/ч. Необходимо определить характер изменения скорости, т.е. рассматривать интервал 40-50 км/ч или 40-30 км/ч.
Задаемся условием: скорость поезда не меняется, т.е. остается постоянной V = 40 км/ч; определяем по характеристике fk - w0 = f (V) (движение в режиме тяги) величину равнодействующей удельных сил для скорости 40 км/ч - точка “d1” и, соответственно, fk - w0 = 2,5 Н/кН. Определим знак и значение равнодействующей силы 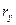 , действующей на поезд, при движении по уклону +3,5/ %o в режиме тяги
, действующей на поезд, при движении по уклону +3,5/ %o в режиме тяги 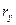 =
= 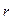 - i = 2,5 - 3,5 = -1 Н/кН. Следовательно, скорость поезда при движении по уклону +3,5 %о будет снижаться и для дальнейших построений нужно выбирать интервал D V = 40 - 30 км/ч. Нетрудно заметить, что при достижении поездом скорости 30 км/ч его движение будет равномерным, т.к. ry = 3,5 - 3,5 = 0 (точка "d1" на рис. 4).
- i = 2,5 - 3,5 = -1 Н/кН. Следовательно, скорость поезда при движении по уклону +3,5 %о будет снижаться и для дальнейших построений нужно выбирать интервал D V = 40 - 30 км/ч. Нетрудно заметить, что при достижении поездом скорости 30 км/ч его движение будет равномерным, т.к. ry = 3,5 - 3,5 = 0 (точка "d1" на рис. 4).
На кривой V = f (S) в точках перелома нужно отметить режимы управления локомотивом: РТ. ХХ. ТР. Режим работы локомотива проставляется в начале интервала изменения скорости.
3. Порядок выполнения задания
1.В соответствии с таблицей удельных равнодействующих сил (прил. 3) и результатами расчета веса поезда (задание 2) на планшет со спрямленным профилем (задание 1) в заданном масштабе нанести графические зависимости удельных ускоряющих fk - w0 =f (V) и замедляющих wox =
f (V), 0,5bT + wox = f (V) сил, действующих на поезд.
2. По кривым удельных ускоряющих и замедляющих сил, используя графический способ А.И. Липеца, на том же планшете построить кривую скорости u = f (S) .
3. Все графические построения выполняются карандашом на листе миллиметровой бумаги размером 210х400.
ЗАДАНИЕ 4.ОПРЕДЕЛЕНИЕ ВРЕМЕНИ ХОДА ПОЕЗДА ПО УЧАСТКУ
СПОСОБОМ Г.В. ЛЕБЕДЕВА
Для расчета времени хода поезда по участку имеются много различных способов, из которых на практике наиболее часто применяют: графический способ Лебедева Г.В, и численный - с помощью ПЭВМ.
Имеются также более грубые (приближенные) методы: способ равновесных скоростей, Унрейна, Дегтярева-Мюллера.
При выполнении задания 4 студентам предлагается определить время хода поезда по участку А-В или В-А (см. задание 1) двумя методами: графическим способом Лебедева Г.В. и способом равновесных скоростей.
1.Основные положения метода ЛЕБЕДЕВА Г.В.
Способ Лебедева Г.В. является графическим методом и основан на следующем геометрическом свойстве кривой t =
f (S): угол, образованный касательной к кривой t = f (S) с осью времени, пропорционален средней скорости движения поезда на данном интервале пути DS (при соответствующем выборе масштабов).
В таблице 5 приведены масштабы величин, которые рекомендуются для практического применения при выполнении задания 4.
Кривая времени t = f (S) строится по кривой скорости V = f (S) на общем планшете с ранее выполненными графическими построениям.
Предположим, что на участке Vk - Vн (рис. 6) скорость,
D V изменяется по линии АВ, а время хода Dt по ав, при этом поезд проходит путь DS. Из треугольника авс получим
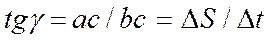 (23)
(23)
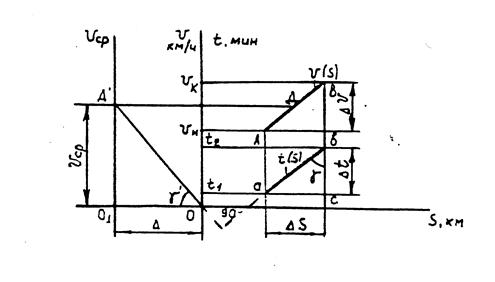 |
Рис. 6. Принцип построения кривой времени (способ
Г.В. Лебедева)
По определению, DS/Dt=ucp, следовательно, интенсивность изменения кривой времени t = f (S) будет зависеть от среднего значения скорости ucp, на участке АВкривой V = f (S).
Построим в масштабе треугольник OO1Д, высота которого будет равна Vср, а основание — постоянной времени D. Из рис. 6 следует, что значения углов g и g/ зависят только от Vср и соотношения масштабов скорости m, времени хи пути у. Приравенстве углов g = g/ построение кривой времени можно производить с помощью линейки и угольника.
2.Порядок построения кривой
1.Кривую скорости разбивают на отдельные участки: ОС1, С1С2, С2С3 и т.д. (рис. 7), как правило, определяемые точками перелома кривой V = f (S), и для каждого участка по равенству Vср = (Vнi + Vкi ) / 2 определяют среднюю скорость (т. Д1,Д2 и т.д.).
2. Влево от т. О по оси S откладывают отрезок О1О2, равный постоянной времени D = 30 мм, и через т. О1 проводят ось средних скоростей Vcp, на которую затем проектируют т. Д1, Д2 и др.
3. Соединяя т. Vср1, Vср2 и другие с началом основания треугольника, т.е. т. О2, лучами Vср1О2, Vср2О2 и другими,находят углы 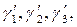 и т.д.
и т.д.
4. Для построения t = f (S) достаточно к лучам Vср1О2, Vср2О2 и другим последовательно восстановить перпендикуляры 0-1, 1-2 и т.д. На практике лучи Vср1О2, Vср2О2 и другие не строятся, а к точкам, например, Vср1 и О2 прикладывается линейка, к которой с помощью угольника из т. О восстанавливается перпендикуляр 0-1 до конца первого интервала изменения пути DS1. Аналогично строится кривая времени на втором интервале изменения скорости (пути), только перпендикуляр 1-2 восстанавливается уже из т. 1 и т.д.
5. Для уменьшения размера планшета и удобства расчетов кривую времени при достижении 10 мин. обрывают (т. 3/ отрезка 2-3) и переносят в начало координат (т. 3//), а затем построение t = f (S) продолжают (рис.7, отрезок 2-3).
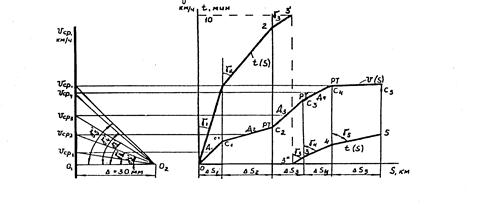
Рис. 7 Техника построения кривой времени
(способ Лебедева Г.В.)
Определив время хода поезда по участку методом Лебедева Г.В., следует рассчитать среднюю техническую Vт и участковую Vуч скорости движения поезда (км/ч):
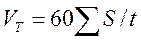 ; (24)
; (24)
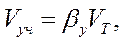 . (25)
. (25)
где: 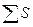 - общая длина профиля, км (из задания 1);
- общая длина профиля, км (из задания 1);
t - время хода поезда, мин;
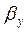 - коэффициент участковой скорости; можно принять b = 0,8-0,9.
- коэффициент участковой скорости; можно принять b = 0,8-0,9.
| <== предыдущая страница | | | следующая страница ==> |
| ПРИМЕРНЫЕ ТЕМЫ УИРС. Темы УИРС выдаются преподавателями кафедры вместе с заданием по подготовке курсовой работы по личному желанию студентов | | | Общее время движения поезда по перегону, мин |
Дата добавления: 2014-09-08; просмотров: 1787; Нарушение авторских прав

Мы поможем в написании ваших работ!