Простые проценты

Основные понятия финансовых методов расчета

Лекция 1. Наращение и дисконтирование по простым и сложным процентным ставкам

Особенностью всех финансовых расчетов является временная ценность денег, т.е. принцип неравноценности денег, относящихся к разным моментам времени. Предполагается, что полученная сегодня сумма обладает большей ценностью, чем ее эквивалент, полученный в будущем, т. е. будущие поступления менее ценны, чем современные. Неравноценность одинаковых по абсолютной величине сумм связана, прежде всего с тем, что имеющиеся сегодня деньги могут быть инвестированы и принести доход в будущем.

Основными понятиями финансовых методов расчета являются:

· процент –абсолютная величина дохода от предоставления денег в долг в лю­бой его форме;

· процентная ставка –относительная величина дохода за фиксированный ин­тервал времени, измеряемая в процентах или в виде дроби;

· период начисления –интервал времени, к которому приурочена процентная ставка;

· капитализация процентов –присоединение начисленных процентов к основ­ной сумме;

· наращение –увеличение первоначальной суммы в связи с капитализацией;

· дисконтирование –приведение стоимостной величины, относящейся к буду­щему, на некоторый, обычно более ранний, период времени (операция, обратная наращению);

· реальная стоимость денег –то количество потребительских благ, которое можно приобрести в обмен на определенную денежную сумму;

· индекс инфляции –среднегодовой индекс прироста потребительских цен.

Существуют различные способы начисления процентов. За основу берется база начисления процентов.Применяют­ся:

· постоянная база для расчета,

Наращенная сумма ссуды (долга, депозита, других видов выданных в долг или инвестированных денег) – это первоначальная ее сумма с начисленными процентами к концу срока начисления.

К наращению по простым процентам обычно прибегают в двух случаях:

1) при выдаче краткосрочных ссуд (сроком до 1 года)

2) в случае, когда процент не присоединяется к сумме долга, а периодически выплачивается

Пусть:

Р – первоначальная сумма долга,

I – проценты за весь срок ссуды,

S – наращенная сумма в конце срока,

i – cтавка простого процента, десятичная дробь (в годовом исчислении),

п – срок ссуды (в годах)

Тогда:

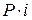– начисленные проценты за один год,

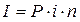– начисленные проценты за весь срок,

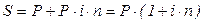– сумма, образовавшаяся к концу срока

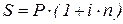– формула простых процентом множитель 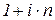– множитель наращения простых процентов

Эта формула предусматривает постоянную процентную ставку на протяжении всего срока погашения процентов. Однако часто используются переменные процентные ставки. Тогда формула простых процентов имеет вид:

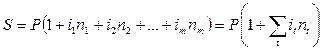
где 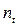– продолжительность периода с постоянной процентной ставкой .

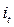Практика расчета по простым процентам используется при выдаче кратковремен­ных ссуд и на период не больше года, так что п может быть и меньшим 1. В этом случае:

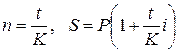где t – количество дней, на которые взята ссуда, K — количество дней в году.

Обе эти величины могут браться как точно, так и приближенно.

Величина t. При точномопределении количества дней подсчитывается число дней между датой выдачи ссуды и датой ее возврата, причем день выдачи и день возврата считаются одним днем. При приближенномопределении количества дней ссуды подсчитывается число полных месяцев между датой выдачи ссуды и датой ее возврата и количество дней сверх полного месяца. Количество дней в каждом месяце принимается равным 30.

Величина K. Точноеколичество дней соответствует 365 или 366. Чаще всего в банковских операциях используется приближенноеколичество дней, равное 360. Процент, подсчитанный с таким числом дней, называется коммерческим,или обыкновенным.

Таким образом, в коммерческой практике применяются три вида процентов:

• точные проценты с точным числом дней в году и точным числом дней ссуды

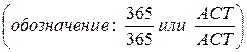
• коммерческие проценты с точным числом дней ссуды

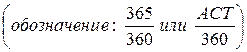
• коммерческие проценты с приближенным числом дней ссуды

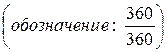
Пример 1. Предположим, Вы берете в банке ссуду в размере 100 млн. рублей на два года. Ставка составляет 30% годовых. Необходимо определить проценты за весь срок ссуды и сумму, образовавшуюся к концу срока ссуды.

Решение.

Из условия имеем: P = 100 000 000, n=2, i=0,3

Тогда: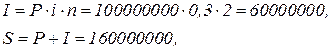

т. е. проценты за весь срок ссуды составляют 60 млн. рублей, а сумма, образовавшаяся к концу срока ссуды, равна 160 млн. рублей.

Пример 2. Контракт предусматривает следующий порядок начисления процентов: первый год – 16%, в каждом последующем полугодии ставка повышается на 1%. Необходимо определить множитель наращения за 2,5 года.

Решение.

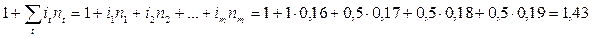
Пример 3. Ссуда в размере 1 млн. рублей выдана 20.01. до 05.10. включительно под 18% годовых. Какую сумму должен заплатить задолжник в конце срока при начислении простых процентов? Год не високосный. При решении применить 3 метода начисления процентов.

Решение.

Имеем: i=0,18

Определим число дней ссуды t: точное – 258, приближенное – 255.

1) Точные проценты с точным числом дней в году и точным числом дней ссуды:

2) Коммерческие проценты с точным числом дней ссуды:

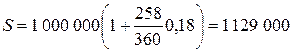
3) Коммерческие проценты с приближенным числом дней ссуды:

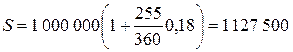
Пример 4. Банк принимает вклады на срочный депозит на срок 3 месяца под 11% годовых. Рассчитать доход клиента при вложении 100 000 рублей на указанный срок.

Решение.

Имеем: P=100 000, t=90, i=0,11.

Сумма, полученная через 3 месяца: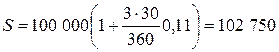

Доход клиента: 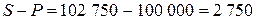рублей.

Пример 5. Банк выдал ссуду на сумму 1 млн. рублей клиенту А на срок 2 месяца, затем деньги, полученные от клиента А, выдал клиенту В на срок 3 месяца. Деньги, полученные от клиента В, выдал клиенту С сроком на 5 месяцев, наконец, деньги полученные от клиента С – клиенту Dна 2 месяца. Все ссуды были даны под 70% годовых. Какую сумму вернет банку клиент D.

Решение. Будем считать, что в месяце 30 дней, в году 360 дней.

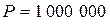
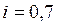
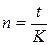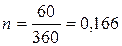
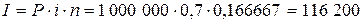
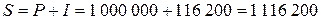
Расчет для клиента А: ,	Расчет для клиента B:
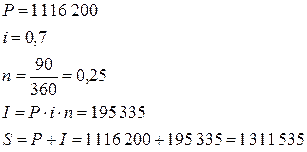
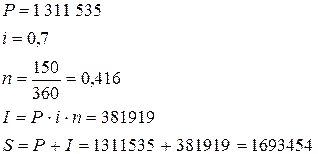
Расчет для клиента C:	Расчет для клиента D:

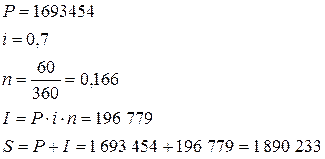
Клиент D вернет банку 1890233 руб.

Дата добавления: 2014-02-26; просмотров: 942; Нарушение авторских прав

Мы поможем в написании ваших работ!