
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ВЗАИМОДЕЙСТВИЕ ЗАРЯЖЕННЫХ И НЕЙТРАЛЬНЫХ ЧАСИЦ С ВЕЩЕСТВОМ
1.1. Взаимодействие заряженных частиц с веществом.
В основе работы любого детектора излучения лежит энергетический процесс - регистрируемая частица должна тем или иным образом передать часть или всю свою энергию рабочему веществу детектора. Эта переданная энергия далее трансформируется в веществе таким образом, чтобы ее выделение можно было зарегистрировать - в виде электрического сигнала, в виде световой вспышки, в виде дефекта кристаллической решетки и т.п.
Заряженные и нейтральные частицы взаимодействуют с веществом принципиально по-разному.
Заряженные частицы теряют свою энергию путем электромагнитного взаимодействия с атомами или молекулами среды  по трем основным каналам:
по трем основным каналам:
- потери на ионизацию и возбуждение атомов или молекул вещества, объединенные в общий канал потерь – ионизационные потери;
- потери на тормозное излучение;
- потери на черенковское излучение.
Ионизационные потери. При движении заряженной частицы через вещество независимо от агрегатного состояния вещества (газ, жидкость, твердое тело) кулоновское взаимодействие электрического заряда частицы с атомами или молекулами вещества приводит к ионизации этих атомов или молекул, или их возбуждению. Для описания этих потерь энергии вводится суммарная характеристика (dE/dx)ион - удельные ионизационные потери. Удельные ионизационные потери измеряются в МэВ/см или в МэВ·см2/г. Последняя величина получается путем деления (dE/dx)ион в Мэв/см на плотность вещества r в г/см3 и удобна тем, что, например, для газов она не зависит от давления газа.
Проведем сравнительно простой расчет удельных ионизационных потерь для нерелятивистской частицы с массой, превосходящей массу электрона.
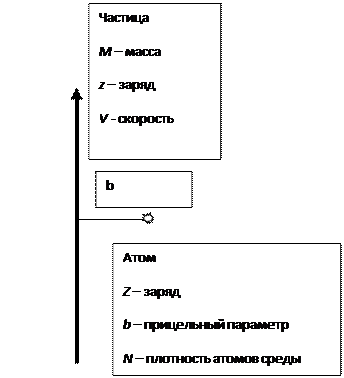
Рис.1. Взаимодействие заряженной частицы с атомом среды
Пусть частица с массой М и зарядом z движется со скоростью v снизу вверх. Рассмотрим взаимодействие электрического поля этой частицы с отдельным электроном среды, где Z – заряд одного атома (молекулы) среды, N – плотность атомов в единице объема, b – прицельный параметр (минимальное расстояние, на которое частица приближается к атому). Среду полагаем невзаимодействующей и неупорядоченной. Последнее замечание применимо практически к любой среде, поскольку направление движения частицы носит случайный характер, а энергия взаимодействия атомов или молекул в любой среде мала по сравнению с энергией частицы. Особый случай составляет лишь сфокусированное движение частицы вдоль кристаллической оси кристалла, что может быть достигнуто в специально поставленных экспериментах. Итак, при сформулированных условиях сила взаимодействия между электрическим полем частицы и отдельным электроном атома среды равна:
 F = ze2/b2 (1).
F = ze2/b2 (1).
Где е – заряд электрона 
За время взаимодействия, равное по порядку величины dt = 2b/V, электрон среды получит (а частица, соответственно, потеряет) импульс, равный
dp = F·dt = 2ze2/bV,
что соответствует приобретенной электроном (и потерянной частицей) энергии dE = (dp)2/2m, где m – масса электрона.
Таким образом, dE = 2z2e4/b2mV2 (2).
В кольцевом слое радиусом «b», шириной db и толщиной dx содержится электронов Ne = ZN·2πb·db·dx..
Тогда полная передача энергии на кольцевой слой будет равна:
(dE/dx) = (4πz2e4ZN/mV2)·(db/b) (3)
Откуда удельные ионизационные потери энергии заряженной частицы на единицу пути dx будут равны:
dE/dx = 
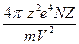


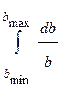
dE/dx = 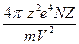 ln(bmax/bmin) (4)
ln(bmax/bmin) (4)
Каков физический смысл пределов интегрирования bmax и bmin?
При упругом взаимодействии тяжелой частицы с электроном максимально возможная передача энергии от тяжелой частицы к электрону из кинематических соображений равна Emax = 2mV2, что соответствует минимальному прицельному параметру bmin. Максимальному прицельному параметру обычно ставят в соответствие некоторую среднюю передачу энергии от частицы к атому, которая носит название «средний ионизационный потенциал». Средний ионизационный потенциал обычно обозначается как I с черточкой: «Ī». Он примерно равен kZ, где k ~ 10 эВ.
Учитывая, что (dE/dx) ~ (db/b), заменим bmax/bmin на Emax./Emin.
Таким образом, окончательно формула для удельных ионизационных потерь для нерелятивистских частиц тяжелее электрона выглядит следующим образом:
(dE/dx)ион = 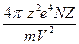 ln(2mV2/ Ī) (5)
ln(2mV2/ Ī) (5)
Где: 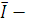 средний ионизационный потенциал (эмпирическая величина, берется из справочников). Следует подчеркнуть, что средний ионизационный потенциал
средний ионизационный потенциал (эмпирическая величина, берется из справочников). Следует подчеркнуть, что средний ионизационный потенциал 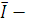 это эмпирическая подгоночная величина, не имеющая ничего общего с потенциалом ионизации атома Iион ,значение которого является конкретной физической величиной, равной энергии, необходимой для удаления валентного электрона атома на бесконечность.
это эмпирическая подгоночная величина, не имеющая ничего общего с потенциалом ионизации атома Iион ,значение которого является конкретной физической величиной, равной энергии, необходимой для удаления валентного электрона атома на бесконечность.
Согласно формуле (5), удельные ионизационные потери зависят от заряда и скорости частицы как z2/V2 (пренебрегая логарифмической зависимостью) и не зависят от массы частицы. Они также зависят от заряда вещества Z и от плотности вещества N.
Особо обращает на себя внимание тот факт, что удельные ионизационные потери не зависят от массы частицы, и, следовательно, все однозарядные частицы, летящие с одинаковой скоростью, будут иметь одинаковые удельные ионизационные потери независимо от их масс.
Однако надо иметь в виду, что привычной шкалой по оси абсцисс обычно является не шкала скоростей, а шкала энергий, и частицы равных энергий будут иметь тем большие потери, чем больше их масса.
В релятивистском случае формула для ионизационных потерь выглядит несколько сложнее. В нее добавляются дополнительные члены, приводящие к медленному росту (dE/dx 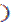 ион с увеличением скорости частицы из-за Лоренцова сокращения электрического поля частицы вдоль направления ее движения и вытягивания поля поперек направления движения. С увеличением скорости частицы в области релятивистских скоростей релятивистский рост замедляется (но не прекращается) из-за экранировки далеко отстоящих от траектории частицы атомов более близко расположенными (эффект плотности), поэтому в более плотных средах рост происходит медленнее, чем в менее плотных.
ион с увеличением скорости частицы из-за Лоренцова сокращения электрического поля частицы вдоль направления ее движения и вытягивания поля поперек направления движения. С увеличением скорости частицы в области релятивистских скоростей релятивистский рост замедляется (но не прекращается) из-за экранировки далеко отстоящих от траектории частицы атомов более близко расположенными (эффект плотности), поэтому в более плотных средах рост происходит медленнее, чем в менее плотных.
Для всех частиц и во всех средах значение ионизационных потерь в минимуме (при кинетической энергии, примерно равной массе покоя частицы) мало отличается друг от друга.
Вид полной зависимости (dE/dx 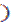 ион от энергии частицы для частиц разной массы приведен на рис.2.
ион от энергии частицы для частиц разной массы приведен на рис.2.
Рис.2 Удельные потери энергии различных частиц в зависимости от их энергии.
Здесь важно отметить, что при v ~ с следует различать энергию, потерянную частицей в слое вещества толщиной «dx» и энергию, поглощенную в том же слое. Если первая, как отмечено выше, неограниченно растет со скоростью частицы, то вторая выходит на насыщение. Выход на насыщение связан с тем, что энергия, потерянная частицей в слое «dx» уносится из этого слоя быстрыми вторичными электронами [6]. Это обстоятельство очень важно, т.к. ограничивает возможность измерения скорости частицы по величине удельных ионизационных потерь в релятивистской области сравнительно небольшим диапазоном скоростей.
Все наши рассуждения не касались удельных ионизационных потерь электронов. Из-за тождественности частиц с электронами дело обстоит несколько сложнее. Действительно, при лобовом соударении налетающий электрон может передать всю свою энергию покоящемуся. Но с точки зрения наблюдателя никакого столкновения как бы и не было! Поэтому при расчетах обычно полагают, что вторичный электрон (электрон отдачи) всегда имеет энергию меньше, чем первичный. Расчеты, проведенные при этих условиях, приводят к сложным формулам, численно отличающимся от формул для тяжелых частиц не более чем на 10%. Но и сама формула (5) обычно дает точность не более нескольких процентов, так что разница оказывается малосущественной. Гораздо более существенно то, что уже при малых энергиях всего в несколько МэВ для электронов становятся весьма заметными радиационные потери, а при больших энергиях они становятся доминирующими.
Как видно из Рис.2 в области энергии частиц порядка массы покоя удельные ионизационные потери имеют широкий минимум, изменяясь на 10% при изменении энергии частиц на порядок. Частицу с энергией, соответствующей минимуму ионизационных потерь, обычно называют минимально ионизирующей частицей, и очень многие измеренные параметры газов, приведенные ниже, относятся как раз к минимально ионизирующим частицам. Из Рис.2 следует, что в минимуме ионизационных потерь они составляют около 2 МэВ·см2/г – величину, которая обычно принимается при прикидочных расчетах.
Удельные ионизационные потери в первом приближении падают при уменьшении энергии частицы как 1/V2. Однако для тяжелых многозарядных частиц при малых энергиях это соотношение нарушается. Особенно этот эффект выражен для тяжелых осколков деления. Для осколков деления непрерывный захват электронов осколками при их торможении и связанное с этим уменьшение эффективного заряда приводит к уменьшению ионизационных потерь. При торможении многозарядных ионов, эффективный заряд которых не очень велик, может происходить попеременно захват и потеря электронов, отчего удельные ионизационные потери сильно флуктуируют.
Так или иначе, вдоль трека движущейся частицы образуются возбужденные атомы или молекулы, а также положительные ионы вещества (или дырки в твердом теле) и свободные электроны. Свободные электроны
имеют широкий диапазон энергий вплоть до значения максимально передаваемой энергии от тяжелой частицы с массой М  m электрону среды, равной (при v~с) Emax = 2mV2 .
m электрону среды, равной (при v~с) Emax = 2mV2 .
Электроны, обладающие энергией выше потенциала ионизации вещества (для большинства газов порядка 15 эВ) и способные в свою очередь ионизовать вещество, называются d-электронами.
Полная ионизации вещества состоит, таким образом, из двух частей – из первичной ионизации непосредственно на треке частицы и вторичной ионизации на треках d-электронов. Соотношение первичной и вторичной ионизаций в веществе составляет примерно 1:2.
Нетрудно оценить количество d-электронов на единице пути частицы.
Действительно, по формуле (2) энергия вторичного электрона равна
dE = E δ = 2z2e4/b2mV2
Интегрируя по кольцевому слою 2πb·db·dx c плотностью электронов NZ, на единицу длины получим:
dn/dE δ = (2πNZz2e4/mV2)(1/Eδ)2
Откуда число d-электронов с энергиями от E δ до E δ max на единицу длины равно:
N δ = (2πNZz2e4/mV2) · (1/ Eδ – 1/ Eδ max ) (6)
Так, для протона с энергией 10 МэВ максимальное значение энергии d-электрона равно 20 КэВ, а число d-электронов с энергией более 1 КэВ составляет около 5 штук на 1 см пути (в газе при атмосферном давлении).
Пробегом частицы называется длина трека частицы до ее полной остановки. Если пробег частицы укладывается в размер детектора, это означает, что частица полностью потеряла в веществе свою кинетическую энергию. В этом случае, измерив тем или иным способом (о чем речь пойдет ниже) полное количество электронно-ионных пар, образованных частицей «N» и поделив энергию частицы Е на N, мы получим среднюю энергию, идущую на образование одной электронно-ионной пары w = Е/N.
В результате многочисленных исследований было обнаружено, что для всех веществ значение w практически не зависит от параметров частицы и, таким образом, является параметром данного вещества. Именно это обстоятельство открывает возможность измерения энергии, потерянной частицей в веществе, так называемым ионизационным методом. Измерив количество электронно-ионных пар N (величину ионизационного эффекта), и зная значения w, которые измерены для всех практически важных веществ, мы можем определить энергию частицы по простой формуле:
Е = wN; (7)
Значения w для некоторых веществ, наиболее часто используемых в качестве рабочих веществ детекторов, приведены в таблице 1.
Табл.1
| В-во | Аr (газ) | СО2 (газ) | Si | Ge | C(алмаз) |
| w,эВ | 3,6 | 2,9 | 13,6 |
Для грубой оценки w для газов обычно принимают равным 30 эВ.
Рассмотрим структуру трека минимально ионизирующей частицы.
Принимая, что потери энергии минимально ионизирующей частицы равны 2 МэВ.см2/г, а плотность газа (воздуха) при атмосферном давлении равна примерно 10-3 г/см3, получим, что на 1 см пути в воздухе при атмосферном давлении частица теряет 2·10-3 МэВ/см или 2 КэВ/см. Считая w равной 30 эВ, получим для 1 см трека релятивистской частицы примерно 70 электронно-ионных пар. Учитывая неравномерность распределения этих пар вдоль трека, а именно то, что на первичную ионизацию приходится лишь 30% актов ионизации, а остальные 70% – на вторичную ионизацию на треках d-электронов, нетрудно видеть, что трек релятивистской частицы в газе очень разрежен – на одном сантиметре трека содержится 20-25 ионизационных кластеров, в каждом из которых содержится от 1 до 3-4 тесно расположенных электронно-ионных пар. В прямую противоположность этому трек тяжелой медленной частицы в плотной среде (например, в твердом теле) представляет собой практически непрерывный плазменный шнур со сплошной ионизацией вдоль трека.
В случае релятивистских частиц обычно их пробеги существенно превышают размеры детектора. Тогда можно считать, что потери энергии частиц в детекторе пропорциональны удельным ионизационным потерям, что открывает возможность определения скорости частицы (т.к. удельные ионизационные потери не зависят от массы частицы)
Поскольку частица по мере ее прохождения через вещество непрерывно замедляется, а удельные ионизационные потери энергии растут с уменьшением скорости частицы как 1/V2, потери энергии частицы резко возрастают в конце пробега (пик Брэгга).
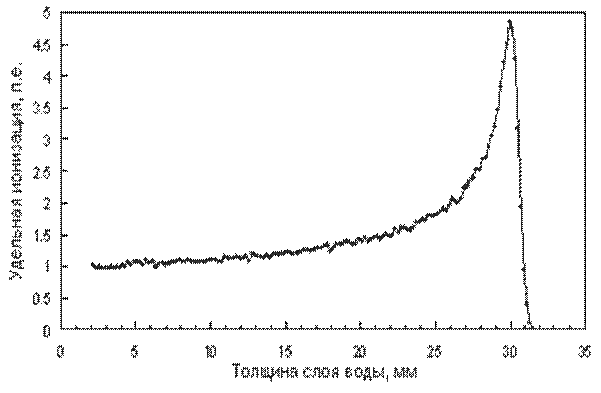
Рис. 3. Пик Брэгга при прохождении протонов с энергией 62 МэВ через воду
На рис.3 приведена зависимость удельной ионизации альфа-частицы в воздухе от пробега (кривая Брэгга).
Это свойство кривой Брэгга широко используется в лучевой терапии. Пробеги протонов и более тяжелых ионов подбирают при облучении пациента таким образом, чтобы максимальное выделение энергии частиц на конце пробега приходилось на злокачественное образование, а поражающий эффект для здоровой ткани был минимальным.
Радиационные потери. Если частица проходит вблизи ядра атома вещества (b << ra), то она в поле ядра испытывает заметное угловое ускорение. В этом случае, согласно законам классической электродинамики, частица должна излучать энергию в виде квантов электромагнитного излучения (тормозное излучение) и, следовательно, терять свою энергию. Величина потерянной энергии пропорциональна квадрату ускорения: (dE/dx)рад ~ а2.
В свою очередь величина ускорения согласно закону Ньютона, обратно пропорциональна массе частицы: а ,  таким образом (dE/dx)рад ~ 1/М2.
таким образом (dE/dx)рад ~ 1/М2.
Сечение испускания фотона с энергией Eγ в первом приближении (без учета малых поправок) выглядит следующим образом:
dσ/dEγ = σrad/ Eγ
откуда (dE/dx)rad = 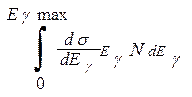 (8)
(8)
При Eγ >> mc2 , Eγ ≈ Eчастицы
Тогда (dE/dx)рад = NE σrad (9)
Величина 1/Nσrad имеет размерность длины и называется радиационной длиной X0.
Как показывает теория (и опыт) σrad не зависит от энергии электронов и является константой при любых энергиях электрона.
Поэтому радиационная длина X0 является константой среды.
Тогда из выражения (9) получим:
(dE/dx)рад = E/X0 , откуда следует, что энергия частицы при прохождении вещества толщиной X следует закону E = E0 exp(-X/X0).
Энергия, при которой ионизационные потери равны радиационным, называется критической энергией. При энергиях частиц выше критической преобладают радиационные потери.
В силу сильной зависимости радиационных потерь от массы частицы при всех достижимых на сегодняшний день энергиях частиц, получаемых на современных ускорителях, радиационные потери пренебрежимо малы по сравнению с ионизационными потерями для всех частиц, тяжелее электрона.
Так для железа критическая энергия электронов равна всего около 12 МэВ, в то время как для мюонов – уже 500 ГэВ.
Потери энергии на черенковское излучение обусловлены процессами поляризации среды, через которую проходит частица. Само черенковское излучение носит пороговый характер и возникает в том случае, когда скорость частицы превышает скорость света в среде, однако поляризация среды такого порога не имеет [7]. Потери энергии заряженной частицы на поляризацию среды невелики, они составляют не более 1% от ионизационных потерь и обычно не учитываются, если речь не идет об использовании излучения Черенкова как такового.
1.2. Взаимодействие гамма-квантов и нейтронов с веществом.
Нейтральные частицы не имеют электрического заряда и, следовательно, не могут непосредственно терять свою энергию путем ионизационных потерь. Однако они взаимодействуют с атомами и ядрами вещества с образованием вторичных заряженных частиц, которым передают всю или часть своей кинетической энергии. Эти заряженные частицы, в свою очередь, ионизируют вещество и могут быть зарегистрированы.
Взаимодействие гамма-квантов с веществом.
Гамма-кванты взаимодействуют с веществом по четырем независимым каналам:
1.Когерентное (Релеевское) рассеяние;
2.Фотоэффект;
3.Комптон-эффект;
4.Рождение электрон-позитронных пар.
5. Фотоядерные реакции.
Каждый из этих процессов характеризуется сечением взаимодействия, зависящим от энергии гамма-квантов и заряда атомов вещества, с которым взаимодействует гамма-квант.
Когерентное (Релеевское) рассеяние – это волновой процесс дифракции гамма-квантов на кристаллической решетке, при котором энергия гамма-квантов не изменяется. Следовательно, не возникает и вторичных заряженных частиц. Он не представляет интереса с точки зрения регистрации гамма-квантов, поскольку энергия гамма-кванта не передается среде, но используется для прецизионного измерения энергии гамма-квантов с последующей регистрацией гамма-квантов, отраженных от кристаллической решетки через фотоэффект, комптон-эффект или рождение электрон-позитронных пар, поскольку энергия отраженных гамма-квантов определяется путем измерения геометрических параметров – постоянной решетки и резонансного угла отражения по формуле Брэгга.
2dsinq=nl (4)
где d - постоянная решетки отражающего кристалла;
q - угол резонансного отражения;
l - длина волны гамма-кванта;
n- порядок отражения (обычно n = 1).
Значения d и q могут быть измерены с очень высокой точностью.
Фотоэффект - это взаимодействие гамма-квантов с наиболее связанными электронами атомов среды. При фотоэффекте гамма-квант поглощается полностью, и закон сохранения энергии выглядит следующим образом:
hν= Ee - Ecв (5)
где: hν – энергия гамма-кванта;
Ее – кинетическая энергия электрона, возникающего благодаря фотоэффекту;
Ecв – энергия связи электрона на K , L или M - оболочке атома.
С наибольшей вероятностью при фотоэффекте происходит взаимодействие гамма-квантов с электронами К-оболочки, обладающими максимальной энергией связи.
Сечение взаимодействия гамма-квантов σфото немонотонно зависит от энергии гамма-квантов, но при энергиях, близких к энергии связи электрона на К-оболочке имеет вид:
sфото = 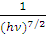 ; (6)
; (6)
Сечение фотоэффекта очень сильно зависит от заряда атома вещества:
sфото ~ Z5 (7)
Атом, потерявший электрон в результате фотоэффекта либо испускает характеристическое рентгеновское излучение, либо Оже-электрон, и таким образом в веществе выделяется вся энергия первичного гамма-кванта.
Комптон-эффект – это упругое взаимодействие (рассеяние) гамма-квантов с наименее связанными (валентными) электронами атомов. При рассмотрении процесса энергией связи электронов с атомом пренебрегают, полагая электроны свободными. Анализ кинематики процесса проводится в релятивистском приближении, поскольку гамма-квант по определению является релятивистской частицей.
Закон сохранения энергии для комптон-эффекта выглядит следующим образом:
 hν= hν' + mec 2(
hν= hν' + mec 2( 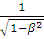 - 1) (8)
- 1) (8)
где hν - энергия первичного гамма-кванта
hν' – энергия рассеянногогамма-кванта
β =V/c
Вводя угол рассеяния q гамма-кванта относительно его первоначального направления, можно получить следующее выражение:
hν' = hν/[1+ 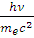 (1 - cosq)] (9)
(1 - cosq)] (9)
Из формулы (8) следует, что при обратном рассеянии гамма-кванта его (минимальная) энергия равна:
hν' = hν /[1+ 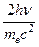 ] (10)
] (10)
Из (9) следует, что, в отличие от фотоэффекта, при комптон-эффекте гамма-квант не исчезает полностью, меняется лишь его энергия. Из этого следует, что кинетическая энергия электрона рассеяния, возникшего в результате комптон-эффекта, всегда меньше энергии гамма-кванта и зависит от угла рассеяния. Максимально возможная энергия рассеянного электрона (комптон-электрона) равна:
(Ее)max= 2 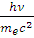 /[1+2
/[1+2 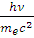 ] (11)
] (11)
Поскольку рассеяние гамма-кванта на тот или иной угол носит случайный характер, энергия рассеянного комптон-электрона не имеет однозначной связи с энергией первичного гамма-кванта hν и,следовательно, комптон-эффект не может быть использован для определения энергии гамма-кванта, если не зафиксирован или не измерен угол рассеяния гамма-кванта q. Сечение комптон-эффекта зависит от энергии гамма-кванта как:
sкомп. = 1/ hν (12)
и от заряда атомов вещества как:
sкомп. = Z (13)
Образование электронно-позитронных пар.
При энергиях гамма-квантов, превышающих пороговое значение, равное двум массам покоя электрона hν>2mec2 (=1,02 МэВ) гамма-квант в поле ядра или в поле электрона может родить электрон-позитронную пару. Закон сохранения энергии в этом случае записывается следующим образом:
hν = 2mec2 + Ee+ + Ee- (14)
где Ее+ и Ее- - кинетические энергии позитрона и электрона соответственно.
Из рассмотрения кинематики процесса рождения пар следует, что электрон-позитронная пара не может быть рождена гамма-квантом в вакууме – не выполняются законы сохранения энергии и импульса. Для рождения гамма-квантом электрон-позитронной пары обязательно требуется наличие поля третьего тела – ядра или электрона среды.
При этом при рождении электрон-позитронной пары в поле ядра, поскольку масса ядра на более чем три порядка превышает суммарную массу электрона и позитрона, кинетическая энергия ядра отдачи пренебрежимо мала, и энергетический порог рождения электрон-позитронной пары практически равен суммарной массе покоя рожденных частиц 2mec2 .
При рождении электрон-позитронной пары в поле электрона атома энергия гамма-кванта распределяется между тремя частицами равной массы, что приводит к повышению энергетического порога рождения пары до величины около 2 МэВ и понижению сечения рождения по сравнению с сечением рождения в поле ядра примерно на порядок.
Поскольку суммарная кинетическая энергия электрона и позитрона рожденной пары однозначно связана с энергией гамма-кванта, ее родившего, она может быть использована для определения энергии гамма-кванта.
Сечение рождения пар на ядрах и электронах зависит от энергии гамма-квантов сложным образом, начиная от пороговых энергий и до энергий порядка 0,5 ГэВ оно возрастает, а при более высоких энергиях остается постоянным и не зависит от энергии гамма-квантов.
Зависимость сечения рождения пар от заряда атомов вещества Z определяется формулой:
sпар ~ Z2 (15)
Все перечисленные выше процессы взаимодействия гамма-квантов с веществом статистически независимы, и полное сечение взаимодействия равно:
sполн = sфото + sкомпт + sпар (16)
Зависимости sфото , sкомпт, sпар и sполн от энергии гамма-квантов приведены на рис.4. Из рисунка видно, что при hu < 0,5 МэВ превалирует фотоэффект, а при hu > 5 МэВ – эффект образования пар.
 Рис. 4. Сечение взаимодействия фотонов с углеродом (Z = 6) и свинцом (Z = 82) при энергиях фотона от 10 эВ до 100 ГэВ. Рис. 4. Сечение взаимодействия фотонов с углеродом (Z = 6) и свинцом (Z = 82) при энергиях фотона от 10 эВ до 100 ГэВ.  ph - сечение фотоэффекта, ph - сечение фотоэффекта,  coh - сечение релеевского рассеяния, coh - сечение релеевского рассеяния,  C - сечение комптоновского рассеяния, C - сечение комптоновского рассеяния,  np - сечение рождения пары в поле ядра, np - сечение рождения пары в поле ядра,  ep - сечение образования пар в поле атомных электронов, ep - сечение образования пар в поле атомных электронов, 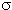 GDR - сечении ядерного фотопоглощения GDR - сечении ядерного фотопоглощения
|
При прохождении потока гамма-квантов через слой вещества толщиной «х» поток ослабляется по закону
Y=Yое-μ х (17)
где Yо – первоначальный поток гамма-квантов
Y – поток гамма-квантов, вышедший из слоя вещества толщиной «х»
μ – линейный коэффициент ослабления,
μ = Nsполн . (18)
где N – число атомов вещества в единице объема в 1/см3;
соответственно Yпогл = Y0 - Y
Формула (17) справедлива только для узкого пучка гамма-квантов.
Величина Yпогл определяет эффективность детектора, т.к. дает число гамма-квантов, поглощенных в веществе (детектора) толщиной «х».
Все приведенные выше формулы для удельных ионизационных потерь, тормозного излучения, сечения взаимодействия гамма-квантов с веществом выведены в предположении, что взаимодействие частиц с веществом носит случайный характер, а атомы среды расположены хаотически относительно трека частицы. Это приближение справедливо и для регулярных кристаллических структур, поскольку трек движущийся частицы расположен случайно относительно атомов кристаллической решетки.
Однако в том случае, если трек сориентирован относительно кристаллической оси или плоскости, т.е. совпадает с направлением этой оси в пределах относительно небольшого угла около 10, картина взаимодействия меняется кардинальным образом. В этом случае частица движется в регулярном потенциале атомов кристаллической решетки, и анализ ее взаимодействия с атомами решетки требует совершенно иного подхода - при небольшом отклонении траектории частицы от направления кристаллической оси трек частицы фокусируется вдоль оси. Этот эффект называется эффектом каналирования.
При каналировании частицы изменяются удельные ионизационные потери, сечение тормозного излучения, сечения рождения пар и ряд других параметров. Так, например, в случае каналирования гамма-квантов в кристалле Si с энергией гамма-квантов 205 ГэВ сечение рождения электрон-позитронных пар возрастает по сравнению со случайным направлением в 15 раз.
Эффект каналирования уже находит практическое применение при фокусировке частиц в ускорителях.
Взаимодействие нейтронов с веществом.
Нейтроны, в отличие от заряженных частиц и гамма-квантов, практически вообще не взаимодействуют с веществом электромагнитным образом. Поэтому единственно возможным каналом взаимодействия является сильное взаимодействие. Простейшим видом сильного взаимодействия нейтронов с ядром является упругое рассеяние нейтронов на ядрах. При рассеянии нейтронов на ядрах возникают ядра отдачи с кинетической энергией, равной:
EA = 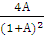 Еncos2φ (19)
Еncos2φ (19)
где ЕА – кинетическая энергия ядра отдачи;
А – массовое число ядра отдачи;
Еn – первоначальная энергия нейтрона;
φ - угол вылета ядра отдачи по отношению к направлению налетающего нейтрона.
При А = 1 (водород) энергия протона отдачи связана с энергией налетающего нейтрона согласно следующей формуле:
Еp =Еn cos2φ (20)
При лобовом ударе (φ = 0) энергия протона отдачи равна энергии налетающего нейтрона :
Еp =Еn,,
т.е. нейтрон полностью передает свою кинетическую энергию протону отдачи.
При рассеянии моноэнергетических нейтронов на протонах спектр протонов отдачи представляет собой равновероятное распределение от 0 до Еn,, так что в среднем нейтрон при столкновении с протоном теряет половину своей энергии.Процесс упругого рассеяния нейтронов на водороде имеет большое сечение (около 10 барн при энергии нейтронов 100 КэВ и плавно падает до 0,1 барн при энергии 100 МэВ) и широко используется при детектировании нейтронов с энергией более или порядка 100 КэВ. При меньших энергиях нейтронов энергия протона отдачи слишком мала, чтобы ее хватило для надежной регистрации нейтронов. Тем более это утверждение справедливо для нейтронов тепловых энергий (Еn = 0,025 еV), которые вообще находятся в тепловом равновесии со средой и, следовательно, ни о каких протонах отдачи речи идти не может.
Для регистрации тепловых, надтепловых и резонансных нейтронов используются экзоэнергетические ядерные реакции. Среди них в первую очередь используются реакции на легкодоступных веществах, имеющие большое сечение и большой выход энергии.
2He3 + n ® p + 1H3 (суммарная кинетическая энергия p и 1H3 составляет 0,77 МэВ);
3Li6 + n ® 2He4 + 1H3 (суммарная кинетическая энергия α-частицы 2He4 и ядра трития 1H3 составляет 4,78 МэВ);
5B10 + n ® 2He4 + 3Li7 (суммарная кинетическая энергия α-частицы 2He4 и ядра лития 3Li7 составляет 2,78 МэВ).
Особенно популярна последняя реакция, т.к. в естественной смеси изотопов бора количество 5В10 составляет 19,8%; сечение взаимодействия тепловых нейтронов с естественной смесью равно s = 758 барн.
Для регистрации тепловых и резонансных нейтронов используются также и другие ядерные реакции (фотоядерные реакции), в частности реакции деления на U235, Pu239 и других тяжелых ядрах.
Особый интерес представляет реакция фоторасщепления дейтона. Порог этой реакции равен всего 2,23 МэВ. Сечение реакции максимально примерно при 4 МэВ и равно около 2 мбарн. При увеличении энергии гамма-кванта сечение плавно падает практически до нуля, поэтому фоторасщепление дейтерия имеет ограниченное применение.
В отличие от заряженных частиц, непрерывно теряющих свою энергию при движении через среду, нейтральные частицы взаимодействуют со средой вероятностно, и эта вероятность зависит от энергии частицы, сечения процесса, количества пройденного вещества и т.д. Поэтому все детекторы характеризуются эффективностью регистрации частиц. При этом если эффективность регистрации заряженных частиц обычно близка к 100%, то эффективность регистрации нейтральных частиц зачастую далека от 100% и зависит от вещества детектора, его размеров, геометрии, энергии регистрируемых частиц и других факторов.
| <== предыдущая страница | | | следующая страница ==> |
| КАТАРАКТА | | | ГАЗОРАЗРЯДНЫЕ ДЕТЕКТОРЫ |
Дата добавления: 2014-10-02; просмотров: 1058; Нарушение авторских прав

Мы поможем в написании ваших работ!