
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Расчет на прочность изгибаемых элементов отдельно стоящих опор
При проектировании несущих конструкций отдельно стоящих опор в первую очередь определяют нагрузки, которые передаются на опору от трубопроводов, а затем последовательно рассчитывают траверсу, колонну, базу колонны и фундамент.
5.1 Нагрузки и воздействия на отдельно стоящие опоры
При расчете отдельно стоящих опор и эстакад необходимо учитывать нагрузки, возникающие при их возведении, эксплуатации и испытании трубопроводов.
Отдельно стоящие опоры и эстакады должны рассчитываться на нагрузки от веса трубопроводов с изоляцией, веса транспортируемого продукта, на горизонтальные нагрузки и воздействия от трубопроводов, нагрузки от веса людей и ремонтных материалов на обслуживающих площадках и переходных мостиках, а также снеговые и ветровые нагрузки, при наиболее неблагоприятном их сочетании.
Все нагрузки, действующие на трубопровод, должны быть приведены к его оси и разложены на составляющие: вертикальную, горизонтальную вдоль трубопровода и горизонтальную поперек трубопровода. Величина распределенной вдоль трубы нагрузки характеризуется её интенсивностью 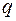

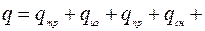 …, (5.1)
…, (5.1)
где  – погонный вес трубы;
– погонный вес трубы; 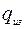 – вес изоляции;
– вес изоляции;
 – вес продукта;
– вес продукта; 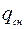 – снеговая нагрузка.
– снеговая нагрузка.
В том случае, если трубопровод проложен по многопролетной схеме (рис. 30), вертикальная нагрузка на одну опору 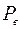 определяется в зависимости от длины пролетов между опорами
определяется в зависимости от длины пролетов между опорами
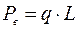 , (5.2)
, (5.2)
где 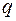 – интенсивность суммарной вертикальной нагрузки на трубопровод;
– интенсивность суммарной вертикальной нагрузки на трубопровод;
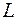 – длина пролета между отдельно стоящими опорами.
– длина пролета между отдельно стоящими опорами.
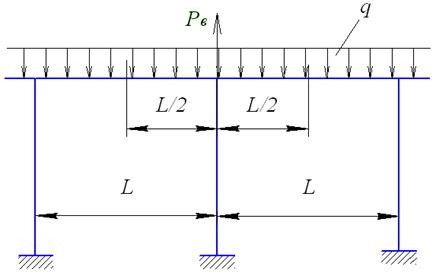
Рис. 30. Расчетная схема для определения вертикальной нагрузки на опору
Нормативная вертикальная нагрузка от трубопроводов на траверсы опор и эстакад должна приниматься по сумме вертикальных нормативных нагрузок от всех трубопроводов (рис. 31).
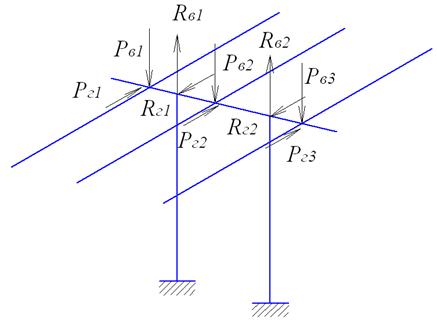
Рис. 31. Определение нагрузок на траверсу от нескольких
технологических трубопроводов
Промежуточные опоры испытывают горизонтальную нагрузку 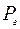 от трубопроводов, которая возникает из-за сил трения в опорном устройстве
от трубопроводов, которая возникает из-за сил трения в опорном устройстве
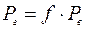 , (5.3)
, (5.3)
где 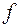 – коэффициент трения, который принимается равным 0,3 для опор скольжения сталь по стали, и принимается равным 0,1 для катковых опор (рис. 27).
– коэффициент трения, который принимается равным 0,3 для опор скольжения сталь по стали, и принимается равным 0,1 для катковых опор (рис. 27).
На рисунке 32 показана расчетная схема траверсы, несущей три технологических трубопровода и опирающейся на две колонны. На этой схеме не учтена нагрузка от собственного веса траверсы.
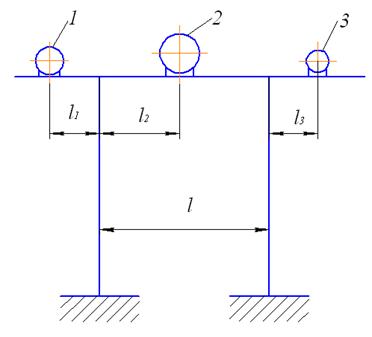
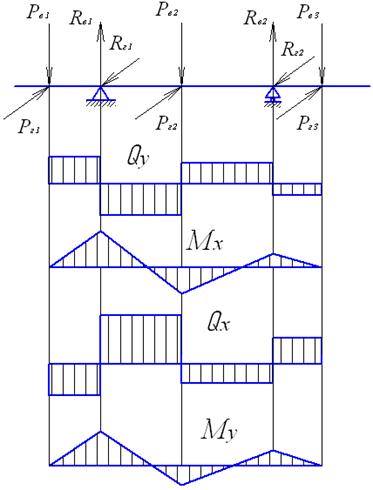
Рис. 32. Расчетная схема траверсы
Чтобы рассчитать траверсу на прочность, её представляют в виде статически определимой балки, изгибаемой в двух плоскостях. Опоры балки находятся в местах установки колонн. Из уравнений статики определяют реакции опор 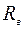 и
и 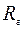 в вертикальной и горизонтальной плоскостях соответственно. После этого строят эпюры поперечных сил
в вертикальной и горизонтальной плоскостях соответственно. После этого строят эпюры поперечных сил 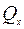 ,
, 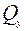 и изгибающих моментов
и изгибающих моментов 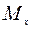 ,
, 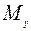 .
.
5.2 Расчет железобетонных траверс
5.2.1. Железобетонные траверсы с одиночной арматурой
В этом случае считается, что предельное состояние наступает, когда внутренние продольные усилия в растянутой стальной арматуре достигают величины, соответствующей пределу текучести материала 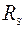 (рис. 33)
(рис. 33)
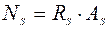 . (5.4)
. (5.4)
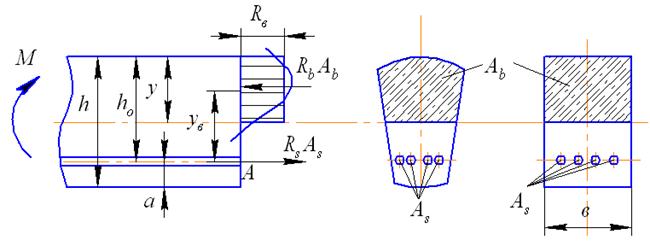
Рис.33. Расчетная схема железобетонной балки с одиночной арматурой
Одновременно, такому усилию в стальной арматуре будет соответствовать прямоугольная эпюра напряжений в сжатом бетоне, т.е. когда в процессе роста нагрузки в результате ползучести бетона напряжения выровняются и достигнут предела текучести 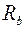 . Соответственно усилие в бетоне будет определяться
. Соответственно усилие в бетоне будет определяться
 . (5.5)
. (5.5)
При расчете на прочность определяют допускаемую величину изгибающего момента в железобетонной балке (траверсе).
Рассмотрим равновесие отсеченной части железобетонной балки, к которой приложен внешний изгибающий момент 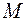 . Определим сумму моментов относительно точки
. Определим сумму моментов относительно точки 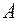 , которую поместим в поперечном сечении на линии действия продольной силы
, которую поместим в поперечном сечении на линии действия продольной силы  в арматуре.
в арматуре.
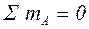 (5.6)
(5.6)
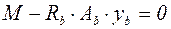 . (5.7)
. (5.7)
Несущая способность железобетонной балки обеспечивается, если внешний момент не превысит величины предельного момента внутренних сил.
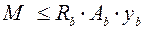 (5.8)
(5.8)
Для элемента прямоугольного сечения (рис. 33)
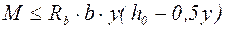 . (5.9)
. (5.9)
Положение нейтральной оси и площадь сжатой зоны определяются из условия равенства нулю продольных сил
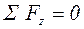
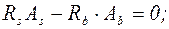
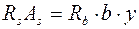 .
.
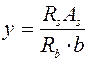 . (5.10)
. (5.10)
5.2.2. Железобетонные траверсы с двойной арматурой
Железобетонные балки с двойной арматурой применяют в том случае, когда изгибающий момент по длине балки меняет знак, т.е. растянутые волокна будут находиться как в верхней, так и в нижней частях балки (рис. 34).
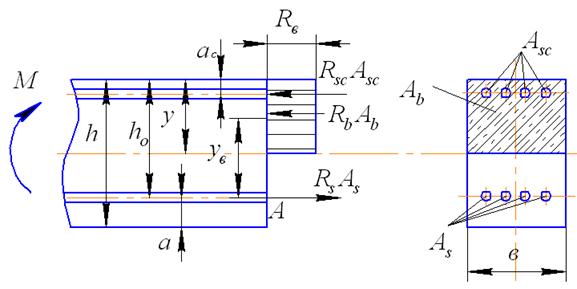
Рис.34. Расчетная схема железобетонной балки с двойной арматурой
В этом случае условие прочности можно также получить из условия равенства моментов относительно точки 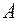
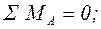
 , (5.11)
, (5.11)
где 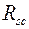 – расчетное сопротивление стали арматуры сжатию;
– расчетное сопротивление стали арматуры сжатию;
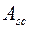 - площадь сечения сжатой арматуры.
- площадь сечения сжатой арматуры.
Положение нейтральной оси и площадь сжатой зоны определяются из условия равенства нулю продольных сил
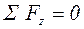
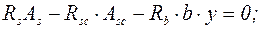
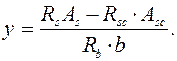 (5.12)
(5.12)
5.3 Расчет стальных балочных конструкций опор и эстакад.
На практике наиболее часто встречаются два варианта конструкций:
· прокатные балки;
· сварные двутавровые балки (составные).
Прокатные балки применяют, как правило, для перекрытия небольших пространств конструктивными элементами. Их несущая способность ограничена номенклатурой выпускаемых прокатных профилей.
В сравнении с составными балками, прокатные балки обладают рядом особенностей:
· они более металлоемки;
· менее трудоемки в изготовлении;
· более надежны в эксплуатации;
· отсутствие сварных швов в области контакта полок со стенкой существенно снижает концентрацию напряжений и возможность возникновения начальных дефектов.
5.3.1 Проверка двутавровой балки на прочность.
Проверку на прочность проводят в тех точках стальных балок, где возникают наибольшие нормальные или касательные напряжения. Кроме того, рассматриваются те опасные места в конструкции балки, где одновременно действуют как нормальные, так и касательные напряжения, так как именно в этих точках может выполняться условие перехода материала в пластическое состояние. Как правило, в поперечных сечениях, где возникают максимальный изгибающий момент 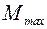 или максимальная поперечная (перерезывающая) сила
или максимальная поперечная (перерезывающая) сила 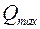 приложены сосредоточенные силы от нагрузок (например: от веса лежащей на балке трубы), в том числе опорные реакции.
приложены сосредоточенные силы от нагрузок (например: от веса лежащей на балке трубы), в том числе опорные реакции.
В поперечных сечениях балки, где изгибающий момент 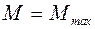 , проверку на прочность выполняют по нормальным напряжениям
, проверку на прочность выполняют по нормальным напряжениям
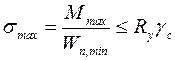 , (5.13)
, (5.13)
где 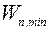 – момент сопротивления сечения нетто;
– момент сопротивления сечения нетто;
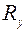 – расчетное сопротивление стали;
– расчетное сопротивление стали;
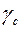 – коэффициент условий работы.
– коэффициент условий работы.
В тех случаях, когда в сечении с максимальным изгибающим моментом действуют еще и значительные поперечные силы, применяют следующую формулу (СНиП II-23-81)
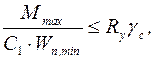 (5.14)
(5.14)
где 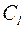 – коэффициент, учитывающий возможность развитие пластических деформаций.
– коэффициент, учитывающий возможность развитие пластических деформаций.
Коэффициент 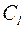 вычисляют следующим образом.
вычисляют следующим образом.
Сначала вычисляют средние касательные напряжения в сечении
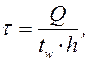 (5.15)
(5.15)
где 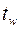 – толщина стенки двутавра;
– толщина стенки двутавра;
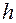 – высота сечения двутавра.
– высота сечения двутавра.
Коэффициент 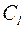 принимается равным
принимается равным 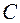 по таблице 5.1, если касательные напряжения
по таблице 5.1, если касательные напряжения 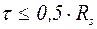 , где
, где  – расчетное сопротивление стали сдвигу.
– расчетное сопротивление стали сдвигу.
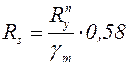 , (5.16)
, (5.16)
где 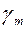 – коэффициент надежности по материалу.
– коэффициент надежности по материалу.
Таблица 5.1
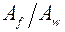
| 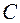
|
| 0,25 | 1,19 |
| 0,5 | 1,12 |
| 1,0 | 1,07 |
| 2,0 | 1,04 |
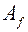 – площадь полки двутавра;
– площадь полки двутавра;
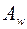 – площадь стенки двутавра.
– площадь стенки двутавра.
Для диапазона 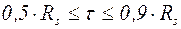 коэффициент
коэффициент 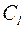 находят в зависимости от значения средних касательных напряжений в сечении
находят в зависимости от значения средних касательных напряжений в сечении 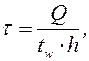
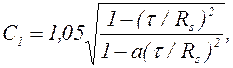 (5.17)
(5.17)
где 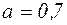 – для двутавров, изгибаемых в плоскости наибольшей жесткости;
– для двутавров, изгибаемых в плоскости наибольшей жесткости;
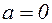 – для других сечений.
– для других сечений.
В сечения, где возникает максимальная поперечная сила 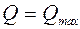 , проверка на прочность проводится по касательным напряжениям (рис. 35).
, проверка на прочность проводится по касательным напряжениям (рис. 35).
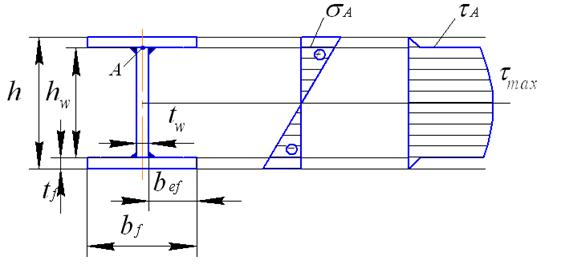
Рис.35. Расчетная схема изгиба стальной двутавровой балки
Для балки произвольного сечения касательные напряжения определяются по формуле Журавского
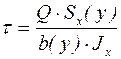 , (5.18)
, (5.18)
где 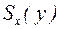 – статический момент отсеченной части сечения;
– статический момент отсеченной части сечения;
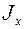 – момент инерции сечения;
– момент инерции сечения;
 – ширина сечения в точке с координатой
– ширина сечения в точке с координатой  .
.
Для двутавра максимальные касательные напряжения возникнут на линии горизонтальной оси симметрии, где 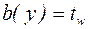
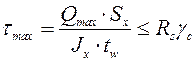 . (5.19)
. (5.19)
Для тех сечений изгибаемых балок, где приложены сосредоточенные нагрузки, а также в опорных сечениях балок необходимо выполнить расчет на срез стенки двутавра
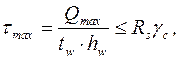 (5.20)
(5.20)
где 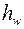 – высота стенки двутавровой балки.
– высота стенки двутавровой балки.
Для расчета на прочность балки в местах приложения нагрузки к верхнему поясу, а также в опорных сечениях балок, не укрепленных ребрами жесткости, следует выполнить проверку на прочность с учетом местных напряжений.
Величина местных напряжений 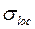 зависит от нагрузки
зависит от нагрузки 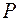 , передающуюся от трубы через опорное устройство, и размеров той площадки стенки двутавра, на которую передается деформация сжатия через изгибаемый пояс двутавра (рис. 36)
, передающуюся от трубы через опорное устройство, и размеров той площадки стенки двутавра, на которую передается деформация сжатия через изгибаемый пояс двутавра (рис. 36)
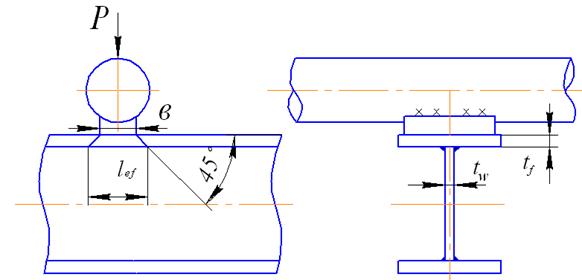
Рис.36. Расчетная схема двутавровой балки на изгиб в месте приложения нагрузки
Условие прочности при проверке только по местным напряжениям
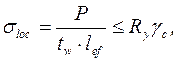 (5.21)
(5.21)
где 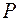 – расчетное значение нагрузки (сосредоточенной силы);
– расчетное значение нагрузки (сосредоточенной силы);
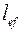 – условная длина распределения локальной нагрузки
– условная длина распределения локальной нагрузки
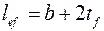 . (5.22)
. (5.22)
5.3.2 Сварные двутавровые балки
Расчет на прочность таких балок проводится аналогично по максимальным нормальным напряжениям 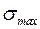 и максимальным касательным напряжениям
и максимальным касательным напряжениям 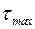 при соблюдении соотношений между конструктивными размерами (рис.33)
при соблюдении соотношений между конструктивными размерами (рис.33)
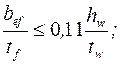
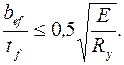 (5.23)
(5.23)
В опасных сечениях, где возникают неблагоприятные сочетания нормальных, касательных и местных напряжений (точки 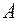 в зоне стенки у пояса) проверку прочности выполняют по
в зоне стенки у пояса) проверку прочности выполняют по 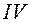 гипотезе прочности (удельной энергии формоизменения).
гипотезе прочности (удельной энергии формоизменения).
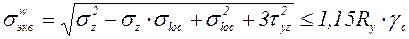 . (5.24)
. (5.24)
В этой формуле 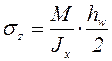 – нормальные напряжения на уровне поясных швов от изгибающего момента
– нормальные напряжения на уровне поясных швов от изгибающего момента 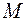 .
.
Касательные напряжения от поперечной силы 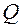
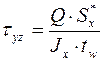 , (5.25)
, (5.25)
где 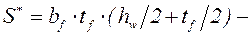 статический момент отсеченной части двутавра;
статический момент отсеченной части двутавра;
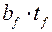 – площадь полки двутавра;
– площадь полки двутавра;
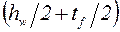 – координата центра тяжести полки относительно центра тяжести сечения двутавра.
– координата центра тяжести полки относительно центра тяжести сечения двутавра.
Если местные напряжения отсутствуют, тогда  .
.
Если это условие не выполняется, стенку балки под сосредоточенной силой укрепляют ребрами жесткости.
5.3.3 Проверка общей устойчивости балки
При изгибе высоких балок с узкими поясами может произойти боковое выпучивание сжатого пояса (рис.37). При этом балка изгибается не только в плоскости действия внешних сил, но и в плоскости min жесткости, вследствие чего происходит скручивание балки.
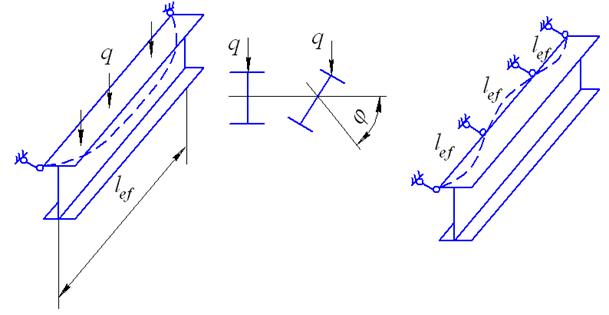
Рис.37. Расчетная схема потери устойчивости сжатого пояса
двутавровой балки при изгибе
Выпучивание происходит на участке между закреплениями верхнего пояса. Расстояния между закреплениями называются расчетной длиной балки 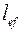 .
.
Расчет на общую устойчивость балок двутаврого сечения выполняют с учетом коэффициента уменьшения допускаемого напряжения на сжатие 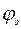 , который зависит от гибкости балки и материала из которого она изготовлена
, который зависит от гибкости балки и материала из которого она изготовлена
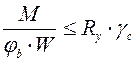 , (5.26)
, (5.26)
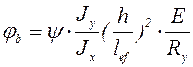 . (5.27)
. (5.27)
где 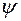 – коэффициент зависящий от характера нагружения, его величину необходимо принимать согласно СНиП II-23-81 «Стальные конструкции».
– коэффициент зависящий от характера нагружения, его величину необходимо принимать согласно СНиП II-23-81 «Стальные конструкции».
Например, для незакрепленного в пролете пояса и сосредоточенной силы
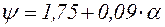 , (5.28)
, (5.28)
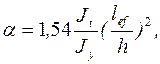 (5.29)
(5.29)
где 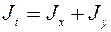 - полярный момент инерции сечения.
- полярный момент инерции сечения.
Общую устойчивость не требуется проверять при отношении 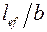 не превышающих критических значений (см. СНиП).
не превышающих критических значений (см. СНиП).
5.3.4 Проверка жесткости балок
Этот расчет относится ко второй группе предельных состояний.
Жесткость балок проверяют по формуле:
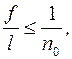 (5.30)
(5.30)
где 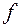 – максимальный прогиб, вызванный нормативной нагрузкой;
– максимальный прогиб, вызванный нормативной нагрузкой;
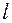 – пролет балки;
– пролет балки;
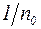 – предельный относительный прогиб.
– предельный относительный прогиб.
Обычно 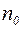 принимается в пределах 200 …400.
принимается в пределах 200 …400.
Например, прогиб однопролетной балки, нагруженной равномерно распределенной нагрузкой:
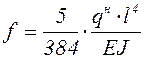 , (5.31)
, (5.31)
где 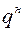 – нормативная погонная нагрузка на балку.
– нормативная погонная нагрузка на балку.
При предельном прогибе и при напряжении равном расчетному сопротивлению, получается выражение для минимально возможной высоты балки:
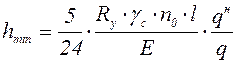 . (5.32)
. (5.32)
где 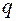 – расчетная погонная нагрузка на балку.
– расчетная погонная нагрузка на балку.
5.3.5 Расчет поясных швов
Рассмотрим расчет непрерывных сварных швов соединяющих стенку двутавра с его поясами.
Сварные швы препятствуют взаимному сдвигу поясов и стенки (рис. 38), вследствие чего в них возникают касательные напряжения. В случае воздействия поперечных сил на двутавр в соответствии с законом парности касательных напряжений усилие на сварной шов будет равно усилию от касательных напряжений в этой точке поперечного сечения (рис. 38).
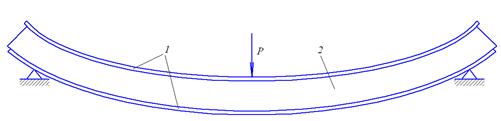
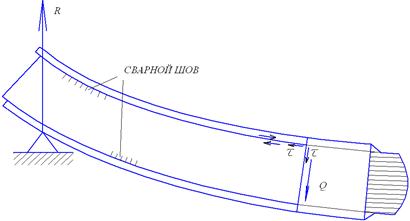
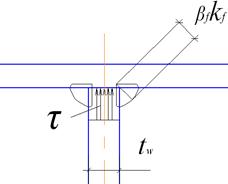
Рис. 38. Расчетная схема сварных швов поясов двутавра
Сдвигающее усилие на единицу длины пояса в соответствии с формулой Журавского
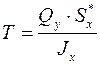 , (5.33)
, (5.33)
где 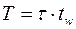 .
.
Условие прочности для поясных швов, воспринимающих сдвигающие усилия
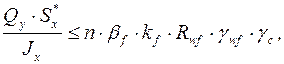 (5.34)
(5.34)
где  – для одностороннего сварного шва;
– для одностороннего сварного шва;
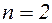 – для двустороннего сварного шва.
– для двустороннего сварного шва.
Отсюда получаем выражение для вычисления величины катета сварного шва
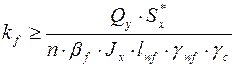 . (5.35)
. (5.35)
5.3.6 Расчет сварных стыков двутавровых балок
Различают сварные стыки балок (рис. 39), выполненные в заводских условиях 1 и монтажные стыки, выполненные при сооружении конструкции на строительной площадке 2.
Заводские стыки выполняют с целью увеличения длины отправочных строительных элементов. Такие стыки имеют несомненные преимущества технологии изготовления, точности и качества соединений.
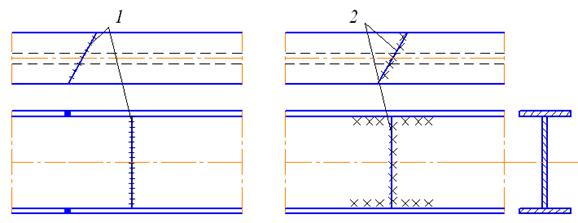
Рис. 39. Стыковка двутавровой балки с помощью сварки
Наиболее простым получается такой стык, когда пояса и стенка стыкуются в одном сечении. Однако он не обеспечивает равнопрочности стыкового сечения с поперечным сечением балки, когда в работе участвует только основной материал.
В связи с этим для достижения равнопрочного стыка:
· располагают стык в сечении, где момент не превышает 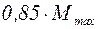 ;
;
· устраивают шов вразбежку.
Увеличение надежности стыка при действии значительных моментов и поперечных сил достигают с помощью горизонтальных накладок, установленных по верхней и нижней полкам, и вертикальных двусторонних накладок по стенке балки (рис.40).
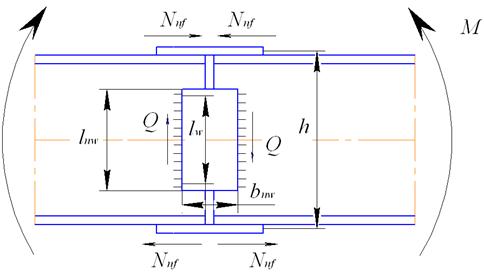
Рис 40. Стык двутавровой балки с помощью накладок
Изгибающий момент представляется парой сил 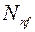 , действующих в срединных плоскостях поясных накладок.
, действующих в срединных плоскостях поясных накладок.
Требуемая площадь сечения поясных накладок:
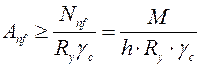 , (5.36)
, (5.36)
где 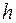 – расстояние между серединами накладок.
– расстояние между серединами накладок.
Ширина накладки принимается на 18-20 мм меньше или больше ширины полки двутавра.
Длину полунакладки находят из условия размещения 2-х угловых швов, рассчитанных на передачу действующего в накладке усилия 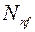 .
.
Поперечную силу в сечении стыка воспринимают накладки на стенке и вертикальные угловые швы.
Суммарная толщина накладок – не менее толщины стенки. Ширина 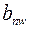 = 150…200 мм.
= 150…200 мм.
Накладки проверяют на срез:
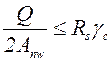 , (5.37)
, (5.37)
где 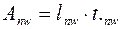 .
.
При расчете катетов вертикальных швов учитывают поперечную силу 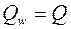 и момент
и момент 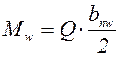 .
.
Условие прочности сварных швов:
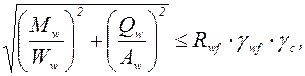 (5.38)
(5.38)
где 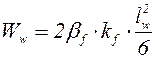 – момент сопротивления сечений сварных швов;
– момент сопротивления сечений сварных швов; 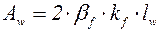 – площадь сечения сварных швов;
– площадь сечения сварных швов;
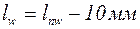 – расчетная длина сварного шва.
– расчетная длина сварного шва.
| <== предыдущая страница | | | следующая страница ==> |
| Конструирование и расчет отдельно стоящих опор | | | Расчет элементов строительных конструкций на сжатие |
Дата добавления: 2014-10-02; просмотров: 1139; Нарушение авторских прав

Мы поможем в написании ваших работ!