
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ НАПРАВЛЯЮЩИХ СИСТЕМ
§1.1 Постоянное и переменное электромагнитное поле. Электромагнитная волна
Постоянное электромагнитное поле.Постоянная разность потенциалов создаёт постоянное электрическое поле напряжённостью Еи постоянное во времени вихревое магнитное поле Н, направленное по правилу правой руки (рис.1.1.).
  | |||
 | |||
Переменное электромагнитное поле.
1) Переменное электрическое поле создаёт вокруг себя вихревое магнитное поле Н, направленное по правилу правого винта.
2) Вихревое магнитное поле изменяется с течением времени (изменяет свое направление вслед за изменением направления вектора 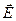 ) создаёт вокруг себя вихревое электрическое поле, направление которого определяется по правилу левой руки (рис.1.2.).
) создаёт вокруг себя вихревое электрическое поле, направление которого определяется по правилу левой руки (рис.1.2.).
§1.2.Электромагнитные процессы в проводных системах. Вектор Умова-Пойтинга.
На потерях энергии при распространении волн всегда сказывается влияние проводников и диэлектриков, встречающихся на их пути.
В проводной системе энергия передаётся за счёт протекания тока проводимости ( 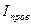 ). Электромагнитное поле возникает из-за движения зарядов по проводнику и изменения магнитного поля во времени (рис.1.3.).
). Электромагнитное поле возникает из-за движения зарядов по проводнику и изменения магнитного поля во времени (рис.1.3.).
В результате внутри проводника происходят волновые процессы, показанные на рисунке 1.2. Эти процессы препятствуют распространению электромагнитной энергии по проводнику, вызывая дополнительные потери.
 |
Введем характеристику количества энергии.
Количество энергии (мощность), распространяющее в единицу времени через плоскость, перпендикулярную направлению потока энергии, выражается величиной
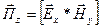 , (1.1.)
, (1.1.)
где 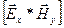 – называется вектором Умова-Пойтинга.
– называется вектором Умова-Пойтинга.
 |
В проводных системах в идеальном случае для того, чтобы возник Пz необходимо
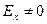 и
и 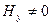 , следовательно, Ez=0.
, следовательно, Ez=0.
Однако вследствие потерь в металле возникает составляющая Ez≠0, которая будет характеризовать величину этих потерь (амплитуда сигнала уменьшается и вдоль оси z возникает разность потенциалов).
§1.3. Электромагнитные процессы в волноводах (диэлектриках).
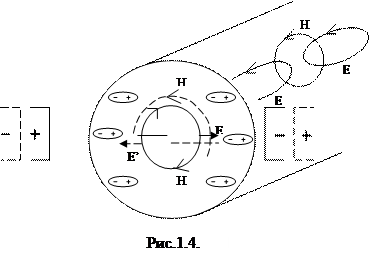
В отличие от проводной системы в диэлектрике отсутствует ток проводимости и энергия передаётся за счёт возникновения тока смещения, т.е. переменной поляризации диполей (рис.1.4.).
 |
Чем выше частота переменной поляризации, тем больше ток смещения.
Выводы:
1) В волноводах энергия передаётся за счёт внешнего изменения электрического поля с течением времени и за счет изменения вихревого магнитного поля.
2) В волноводе Евихр соответствует составляющей Еz, которая характеризует не потери, как в проводных системах, а мощность передаваемой энергии. Еz совпадает по направлению с вектором Пz
3) Для того чтобы поддержать постоянным электромагнитное поле в волноводе необходимо изменять полярность внешнего электрического поля с высокой частотой, иначе произойдут процессы аналогичные разряду конденсатора. При этом должно выполняться условие λ ≤ D, т.к.частота f = υ/λ
где λ – длина волны;
D – диаметр волновода;
υ – скорость распространения электромагнитной волны.
Т.к. распространение электромагнитной энергии по волноводам описывается в рамках волновой теории, то составляющие Еz и Hz будут описывать не потери энергии, а сам процесс распространения энергии по волноводу. Чем больше эти составляющие, тем больше мощность передаваемой энергии.
§1.4. Примеры структуры электромагнитного поля внутри волноводов
Пример №1.
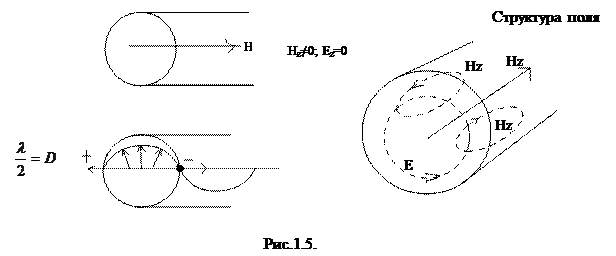 |
Пример №2.
 |
С точки зрения лучевой теории световые лучи, соответствующие структуре электромагнитного поля в приведённых примерах называются меридиальными. Для них одна из составляющих перпендикулярна плоскости волновода, а другая принадлежит плоскости волновода.
Такие лучи, распространяясь по световоду, пересекают его ось.
 |
Структура поля, показанная на рисунке 1.5. (волна типа Н01) обладает лучшими характеристиками, по сравнению со структурой поля на рисунке 1.6. (волна типа Е02). Это объясняется тем, что в первом случае в металлических стенках волновода будет отсутствовать Еz, т.е. ток проводимости.
 Во втором случае электрическая составляющая Еz будет пересекать металлические стенки волновода, вызывая в них ток проводимости, следовательно, дополнительные потери в металле.
Во втором случае электрическая составляющая Еz будет пересекать металлические стенки волновода, вызывая в них ток проводимости, следовательно, дополнительные потери в металле.
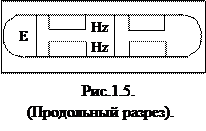 |
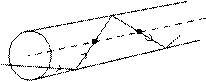
 В световодах, кроме меридиальных лучей, могут распространяться также косые лучи. Они в отличие от меридиальных огибают ось световода по определённой траектории (рис.1.7. Треугольник или многогранник в поперечном сечении).
В световодах, кроме меридиальных лучей, могут распространяться также косые лучи. Они в отличие от меридиальных огибают ось световода по определённой траектории (рис.1.7. Треугольник или многогранник в поперечном сечении).
§ 1.5. Классы электромагнитных волн.
В зависимости от структуры электромагнитного поля различают следующие классы электромагнитных волн: ТЕМ – поперечно-электромагнитная; Е - электрическая или поперечно-магнитная ТМ-волна; Н – магнитная или поперечно-электрическая ТЕ-волна; ЕН, НЕ – гибридные или смешанные. Основные данные по классам волн представлены в таблице 1.
I Поперечная электромагнитная волна.
Передается по проводникам в проводных системах (см. § 1.2.) за счёт тока проводимости, ток смещения присутствует в изоляции и вызывает дополнительные потери.
II Электрическая поперечно – магнитная волна.
Такие волны передаются по световодам и волноводам. Энергия передаётся за счёт тока смещения, при этом возникает в металлических стенках ток проводимости, вызывая дополнительные потери.
III Магнитная или поперечно – электрическая волна.
Такие волны передаются по световодам и волноводам. Определяющим является ток смещения; ток проводимости отсутствует.
IV Смешанные или гибридные волны.
Такие волны передаются по световодам и волноводам. Содержат обе продольные составляющие с преобладанием в поперечном сечении соответственно электрического или магнитного поля.
Таблица 1.1.
| Обозначение класса | Наименование класса | Определяющий ток | Длина волны | Вид направляющей системы | Частота тока | |
ЕZ =0,
НZ =0

| Т, ТЕМ | поперечно-электромагнитная | 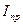 (
( 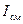 вызывает потери в изоляции) вызывает потери в изоляции)
| λ>D | ВЛС, СК, КК | f↑ потери↑ |
ЕZ ≠0,
НZ =0

| Е | электрическая или поперечно-магнитная | 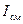 (
( 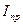 вызывает потери в металлических стенках) вызывает потери в металлических стенках)
| λ<D | МВ | f↑ потери↓ |
ЕZ =0,
НZ ≠0

| Н | магнитная или поперечно-электрическая | 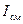
| λ<D | МВ | f↑ потери↓ |
Еz ≠0,
Нz ≠0

| ЕН, НЕ | гибридные или смешанные | 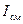
| λ<D | Световоды, диэлектрич. волноводы | f↑ потери↓ |
§ 1.6.Типы (моды) электромагнитных волн.
Наряду с делением на классы электромагнитные волны (кроме ТЕМ) подразделяются также на типы. Тип волны (или мода) определяется сложностью структуры электромагнитного поля в поперечном сечении направляющей системы и обозначается двумя индексами (m, n), которые записываются рядом с обозначением класса.
Например: 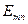 →
→ 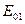 ;
; 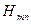 →
→ 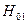 ;
;  ,
,
где для круглых волноводов m – число полных изменений поля по окружности волновода, а n – по диаметру.
В металлических волноводах круглого сечения наиболее перспективна волна 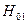 , затухание которой падает с ростом частоты. Электрические силовые линии поля этой волны замкнуты и не соприкасаются со стенками волновода, в которых нет в этом случае токов проводимости и потерь энергии в металле.
, затухание которой падает с ростом частоты. Электрические силовые линии поля этой волны замкнуты и не соприкасаются со стенками волновода, в которых нет в этом случае токов проводимости и потерь энергии в металле.
Волны различных типов можно рассматривать как световые лучи, отличающиеся углом падения и траекторией распространения.
Для меридианных лучей (пересекающих ось световода) индекс m=0, n – показывает число полупериодов (полуволн), укладывающихся вдоль горизонтальной стенки волновода.
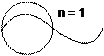 |  | ||
Для косых лучей индекс m ≠ 0. В этом случае m – показывает число полупериодов, укладывающихся вдоль вертикальной стенки волновода или число сторон многоугольника, образованного траекторией луча в торце световода (см. рис.1.7.).
Во всех случаях металлические и диэлектрические волноводы характеризуются так называемой критической частотой 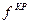 или соответствующей ей критической длиной волны
или соответствующей ей критической длиной волны 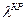 . Волны длиной больше
. Волны длиной больше 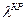 (частотой ниже
(частотой ниже 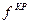 ) по волноводам не распространяются.
) по волноводам не распространяются.
Световоды, по которым распространяются две моды Е01 и Н01, называются одинаковыми. Световоды, по которым распространяются различные моды – многомодовыми.
§1.7. Исходные уравнения электродинамики в векторной форме и их физический смысл.
Исходными уравнениями электродинамики являются уравнения Максвелла, обобщающие два основных закона электродинамики: закон полного тока и закон электромагнитной индукции.
Для однородных сред основные уравнения электромагнитного поля в дифференциальной форме имеют вид:
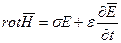 (1.2.)
(1.2.)
 (1.3.)
(1.3.)
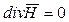 (1.4.)
(1.4.)
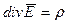 (1.5.)
(1.5.)
где 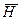 и
и 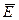 - векторы напряженности соответственно электрического и магнитного полей;
- векторы напряженности соответственно электрического и магнитного полей;
σ - проводимость среды (диэлектрик σ = 0);
ε – диэлектрическая проницаемость среды;
μ – магнитная проницаемость среды;
ρ – объемная плотность электрического заряда;
div (дивергенция)– векторный оператор, характеризующий скорость и количество вытекания частиц;
rot (ротор)– векторный оператор, описывающий изменение вектора по окружности в заданном направлении по правилу правой руки;
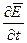 - приращение электромагнитного поля с течением времени t;
- приращение электромагнитного поля с течением времени t;
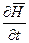 - приращение внешнего магнитного поля с течением времени t.
- приращение внешнего магнитного поля с течением времени t.
Физический смысл уравнений Максвелла:
1) Магнитное поле всегда вихревое (уравнение 1.4), и возбуждается оно как движущимися зарядами, так и изменяющимся во времени электрическим полем (уравнение 1.2).
2) Электрическое поле может быть вихревым (в этом случае оно возбуждается изменяющимся во времени магнитным полем – уравнение 1.3) и безвихревым (если оно возбуждается постоянными во времени электрическими зарядами – уравнение 1.5). Знак минус в уравнении 1.3 указывает на направление электрического поля (правило левой руки). Магнитное поле направлено по правилу правой руки (уравнение 1.2).
При решении конкретных задач должны быть учтены начальные и граничные условия.
§1.8. Уравнение Максвелла для гармонических процессов в комплексной форме.
Для гармонических процессов уравнение Максвелла удобно представлять в комплексной форме.
Гармонический процесс – любой процесс, подчиненный гармоническому закону, например:
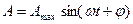
В показательно форме:
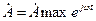
При временной зависимости вида 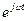 , пользуясь символическим методом, переменное электрическое и магнитное поле изменяются по закону:
, пользуясь символическим методом, переменное электрическое и магнитное поле изменяются по закону:
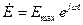
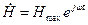
Т.к. первая производная 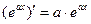 , следовательно
, следовательно 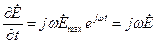
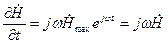
Тогда система уравнений (1.2-1.5) (см.§ 1.7.) будет иметь вид:
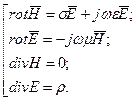 (1.6)
(1.6)
§1.9. Волновые уравнения в векторной форме
Путём математических преобразований из уравнений Максвелла могут быть получены волновые уравнения. Как и уравнения Максвелла, они описывают электромагнитные процессы в любой физической среде. Однако считается, что пространство, где происходят эти процессы, ограниченно и замкнуто (внутри проводника, световода, т.е. направляющей системы). При этом электромагнитная энергия распространяется в заданном направлении (вдоль направляющей системы).
В векторной форме волновые уравнения имеют вид:
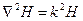
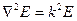
В левой части волнового уравнения находится дифференциальное уравнение, записанное в векторной форме, которое описывает электромагнитные процессы, происходящие внутри проводников или волноводов при передаче энергии ( 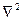 - оператор Лапласа;
- оператор Лапласа; 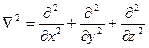 ). В правой части в виде коэффициента распространения среды k сгруппированы параметры среды σ, μ, ε, которые характеризуют материал, из которого изготовлена направляющая система.
). В правой части в виде коэффициента распространения среды k сгруппированы параметры среды σ, μ, ε, которые характеризуют материал, из которого изготовлена направляющая система.
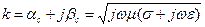 .
.
При помощи коэффициента k может быть рассчитана скорость распространения электромагнитных волн в металле и диэлектрике, например для диэлектрика (σ = 0):
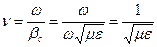 .
.
§1.10 Волновые уравнения в цилиндрической системе координат.
Так как направляющие системы имеют преимущественно форму стержня, то удобнее волновые уравнения записывать в цилиндрической системе координат (координаты r – радиус-вектор; z – координаты по оси z; φ – угол поворота радиус-вектора).

Оператор Лапласа 
в цилиндрической системе координат записывается как:
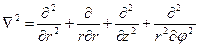
Следовательно, волновые уравнения в цилиндрической системе координат записываются как:
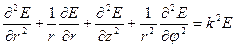

| <== предыдущая страница | | | следующая страница ==> |
| ГЛАВА 3. ОСОБЫЕ (ПРОЦЕССУАЛЬНЫЕ) ВИДЫ ЭКСПЕРТИЗ | | | ГЛАВА II. ТЕОРИЯ ПЕРЕДАЧИ ПО ПРОВОДНЫМ НАПРАВЛЯЮЩИМ СИСТЕМАМ |
Дата добавления: 2014-10-02; просмотров: 770; Нарушение авторских прав

Мы поможем в написании ваших работ!