Теплообмен

4.1 Основы теории передачи теплоты

4.1.1 Виды теплообмена

Теплообменом называется перенос тепла из одной области пространства в другую. Этот перенос может осуществляться с помощью теплопроводности, конвекции и теплового излучения.

Теплопроводностью называется процесс распространения тепла внутри тел посредствам столкновения молекул и путем термодиффузии. Теплопроводность в жидких телах обеспечивается распространением колебательных движений молекул и атомов в направлении менее нагретых областей.

В металлах большое значение в передаче тепла имеют свободные электроны, которые ведут себя подобно одноатомному идеальному газу. Передача тепловой энергии, теплопроводностью реализуется в газах, жидкостях и твердых телах.

Конвекцией называется перенос тепла из одной точки тела в другую частицами тела, перемещающимися в пространстве. Частицы тела в этом случае выполняют роль носителей тепла из области с высокой температурой в область с меньшей температурой. Конвекция может быть только в подвижных средах, т.е. в жидкостях и газах.

Различают свободную и вынужденную конвекцию.

Свободная конвекция проявляется тогда, когда перемещение частиц осуществляется под действием массовых сил (инерции и тяготения) при наличии различной плотности среды в условиях неоднородного температурного поля.

Вынужденная конвекция осуществляется под действием поверхностных сил (давления, трения).

Тепловым излучением тепло может распространяться внутри газов и между твердыми телами в виде электромагнитных волн с различными длинами. Это излучение может поглощаться другими телами, которые вследствие этого нагреваются. Таким образом, процесс излучения тепла в виде электромагнитной энергии называют тепловым излучением.

4.1.2 Температурное поле

В процессе теплообмена каждое тело в каждый момент времени характеризуется определенным распределением температур по всему объему этого тела. Распределение температуры по всему объему тела называется температурным полем данного тела.

В том случае, если это распределение не меняется во времени t, температурное поле называют стационарным, т.е. 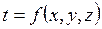, а если меняется, то нестационарным, т.е. 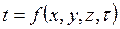(4.1)

В дальнейшем будем рассматривать только такие тепловые процессы, которые характеризуются одномерным, стационарным температурным полем. В этом случае температура каждой точки тела является функцией только одной координаты 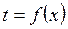. (4.2)

В общем случае температура каждой точки тела при стационарном режиме является функцией координат 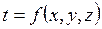. (4.3)

4.1.3 Температурный градиент

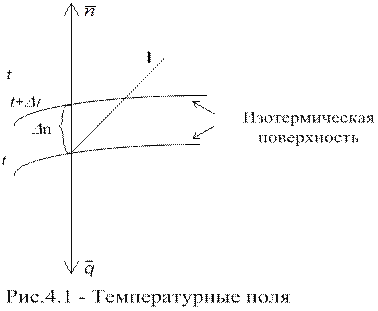
Если соединить все точки тела, обладающие одинаковой температурой, то получим поверхность равных температур, называемой изотермической.

Изотермические поверхности не пересекаются. Изменение температуры в теле наблюдается лишь в направлениях, пересекающих изотермические поверхности. Скорость изменения температуры с расстоянием вдоль какого-либо направления 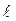характеризуется отношением .

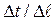Максимальная скорость изменения температуры соответствует направлению нормали n.

Придел отношения приращения температуры 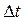к расстоянию между изотермами по нормали 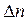называется температурным градиентом.

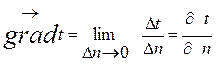(4.4)

Температурный градиент есть вектор, направленный по нормали к изотермической поверхности в сторону возрастания температур. Он имеет размерность .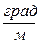

4.1.4 Тепловой поток

Для количественной характеристики процесса распространения тепла вводят понятие о тепловом потоке. Поток энергии, передаваемый частицами более горячего тела частицам тела более холодного, называется тепловым потоком.

Удельным тепловым потоком называется количество тепла, проходящее в единицу времени через единицу площади изотермической поверхности.

Тепловой поток обозначают буквой .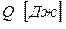

Удельный тепловой поток - .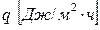

Величина 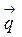является вектором, направление которого совпадает с направлением распространения тепла и противоположно направлению вектора температурного градиента в соответствии с рисунком 4.1.

4.2 Теплопроводность

Явление теплопроводности представляет собой процесс распространения тепловой энергии при непосредственном соприкосновении отдельных частиц тела или отдельных тел, имеющих различную температуру. Теплопроводность обусловлена движением микрочастиц вещества.

4.2.1 Закон Фурье

Опытным путем была установлена и выражена в виде закона зависимость, согласно которой количество тепла 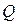, переданного за счет теплопроводности через изотермическую поверхность, зависит от физических свойств тела и пропорционально площади поверхности, времени и температурному градиенту, т.е.

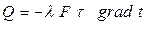, (4.5)

где 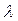- коэффициент теплопроводности, ;

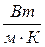F- площадь поверхности, ;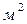

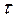- время.

Данная зависимость носит название закона Фурье.

При расчетах иногда пользуются удельным тепловым потоком q, который определяется как

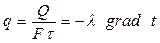(4.6)

В выражении (4.6) стоит знак “минус”. Это значит, что направление вектора 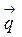противоположно направлению вектора .

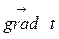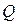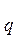Из выражений (4.5), (4.6) видно, что для определения и необходимо знать температурное поле внутри рассматриваемого тела. Нахождение температурного поля и является главной задачей теории теплопроводности.

Коэффициент теплопроводности – это физический параметр вещества. В общем случае он зависит от температуры, давления и рода вещества. В большинстве случаев коэффициент 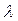для различных материалов определяется опытным путем. Он характеризует способность вещества проводить тепло. Лучшими проводниками теплоты являются металлы, у которых коэффициент 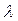изменяется 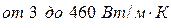; теплопроводность большинства капельных жидкостей 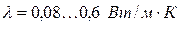; теплопроводность газов .

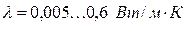Значение коэффициента теплопроводности для ряда материалов дано в таблице 4.1[1].

4.2.2 Теплопроводность плоской стенки

Плоская однослойная стенка толщиной 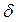разделяет две среды, имеющие различные температуры 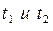, которые устанавливаются на различных поверхностях стенки. Выведем зависимость для температурного поля.

а) Однослойная стенка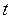

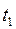
q dx q

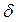
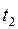
x

x

Рис. 4.2 - Однослойная стенка

внутри стенки и удельного теплового потока, проходящего через стенку. Температурное поле – стационарное, одномерное. Стенка изотропная, коэффициент 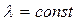, длина и ширина весьма велики по сравнению с ее толщиной.

На расстоянии x двумя изотермическими поверхностями выделим слой толщиной dx. Для него согласно закону Фурье удельный тепловой поток

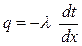(4.7)

Разделив переменные, получим

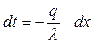(4.8)

Проинтегрируем выражение (4.8) слева 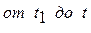и справа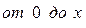

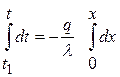
или ,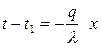

откуда 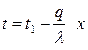(4.9)

При 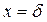; 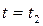из выражения (4.9) получим

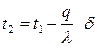
или после преобразований

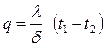(4.10)

Из выражения (4.10) следует, что количество тепла, проходящего через 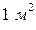плоской стенки в единицу времени, прямо пропорционально коэффициенту теплопроводности и разности температур наружных поверхностей стенки и обратно пропорционально толщине .

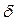Отношение 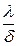- тепловая проводимость стенки; 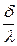- тепловое или термическое сопротивление. Полное количество тепла, переданное через стенку

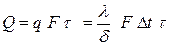(4.11)

В случае, если градиенты температур (dt/dx) в стенке велики, необходимо учитывать изменение коэффициента 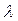в связи с изменением температуры t.

В этом случае вместо 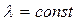принимается

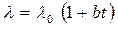, (4.12)

где 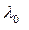- коэффициент теплопроводности при t=0;

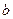- температурный коэффициент, определяемый опытным путем.

б) Многослойная стенка

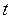
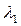
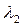
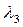
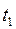
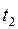
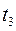q q

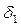
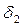
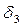
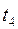
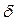
Рис. 4.3 - Многослойная стенка

В теплотехнических расчетах часто приходится определять тепловые потоки и температурные поля для многослойных стенок. Пусть стенка состоит из 3-х плотно прилегающих друг к другу слоев в соответствии с рисунком 4.3. На наружных поверхностях стенки установились постоянные температуры 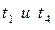. Следовательно, имеет место стационарный режим теплопроводности ( 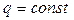для всех слоев).

Примем расчетную схему:

- каждый слой стенки однородный и изотропный;

- величины 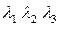постоянны;

- длина и ширина стенки велики по сравнению с ее суммарной толщиной.

При этих условиях температурное поле стенки будет одномерным и стационарным. Температура изменяется в направлении оси 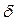. Изотермические поверхности внутри стенки-плоскости, параллельные наружным поверхностям стенки.

Так как величина удельного теплового потока для каждого слоя стенки одна и та же, то можно записать

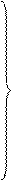
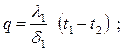
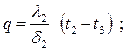(4.13)

,

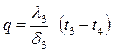отсюда температурные напоры в каждом слое равны

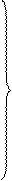
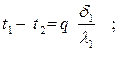
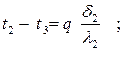(4.14)

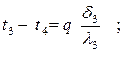
Сложив, левые и правые части выражения (4.14), получим

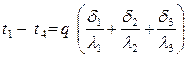. (4.15)

Обозначим 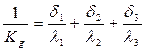- коэффициент теплового сопротивления.

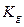- коэффициент теплопроводности многослойной стенки, .

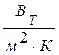Для выражения (4.15) получим

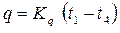(4.16)

Для стенки, состоящей из n – слоев, выражение (4.16) примет вид

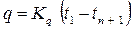, (4.17)

где 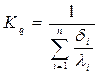(4.18)

Температуры на границе соприкасающихся двух соседних слоев согласно (4.14) равны

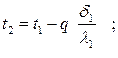
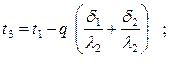
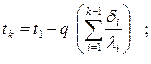(4.19)

На практике часто встречаются цилиндры, толщина стенок которых мала по сравнению с диаметром. В этом случае, допуская небольшую погрешность, расчет теплопроводности их стенок, можно проводить по формулам для однослойной плоской или многослойной стенок. Обычно, при 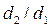меньше 2 погрешность расчета не превышает 4%.

Для многослойной цилиндрической стенки, имеющей n – слоев, не удовлетворяющих выше указанным условиям, т.е. 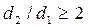могут использоваться зависимости

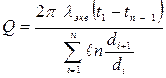, (4.20)

где 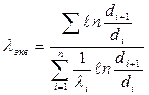(4.21)

Для удельного теплового потока для n – слойной стенки

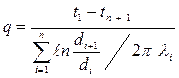(4.22)

Значение температуры на границе между n и n +1 слоями определится из уравнения (4.22) в виде

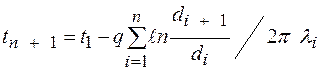(4.23)

4.2.3 Нестационарная теплопроводность плоской стенки

Процессы переноса тепла являются одним из основных разделов современной науки и имеют большой практическое значение в стационарной и промышленной энергетике, в технологических процессах, химической, строительной, лёгкой и других отраслей промышленности. Например, расчёт тепловых аппаратов, работающих при нестандартном режиме, расчёт теплоизоляции зданий, печей, трубопроводов, нагревание машин и др. Исследование кинетики процессов сорбции, сушки, горения и других химико-технологичеких процессов связано с решением задач диффузии, которые аналогичны задачам нестандартной теплопроводимости.

Если температуре поле меняется во времени, то тепловые процессы, протекающие в таких условиях, называют нестандартными.

Нестационарные процессы теплопроводимости встречаются при охлаждении металлических заготовок, прокаливании твёрдых тел, в производстве стекла, общие кирпича, нагревании дерева, вулканизации резины и т.п.

Теплоту при нестационарном режиме можно определить, если найти закон изменения температуры и теплового потока во времени и в пространстве; т.е.

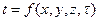и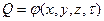

где x, y,z – координаты точки;

τ – время.

Указанные зависимости могут быть найдены из решения дифференциального уравнения теплопроводимости Фурье:

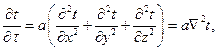(4.24)

где а – коэффициент температуропроводимости, определяемый по формуле

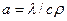(4.25)

(Здесь 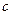– удельная теплоёмкость твёрдого тела; ρ – плотность материала стенки; 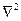- оператор Лапласа; 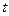- температура).

При решении уравнения (4.24) необходимо задавать граничные условия и начальное распределение температуры в теле (краевые условия).

Граничные условия задаются уравнением вида

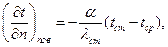(4.26)

где 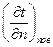- температурный градиент на поверхности;

α – коэффициент теплоотдачи между жидкой средой и поверхностью твёрдого тела;

λ_ст – коэффициент теплопроводности стенки;

t_ст - температура поверхности стенки;

t_ср – температура окружающей среды.

Физические параметры λ, с, ρ считаются постоянными. Температура рассматриваемого тела 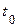в начальный момент времени при τ=0 распределена равномерно, т.е. 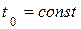. Это может быть температура газов, жидкости, омывающих стенку плоской пластины, цилиндра или шара.

Решение уравнений (4.24) и (4.26) с учётом граничных и временных условий даёт уравнение температурного поля вида

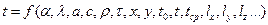(4.27)

Из уравнения (4.27) видно, что температура зависит от большого числа переменных и постоянных параметров и решение его представляет сложную математическую задачу.

Используя теорию подобия и метод размерностей, можно переменные величины сгруппировать в три безразмерных комплекса:

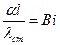- критерий Био;

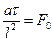- критерий Фурье; (4.28)

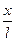- безразмерная координата,

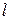– характерный размер тела.

Тогда искомая температура в виде безразмерного комплекса 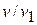может быть представлена следующим уравнением

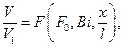(4.29)

где 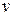– избыточная температура пластины (стенки), равная

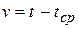
(t – текущее значение температуры стенки;

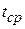– начальная температура окружающей среды);

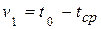(4.30)

разница между начальной температурой стенки и температурой окружающей среды.

Таким образом, температура поверхности стенки цилиндра определяется из соотношения (4.29)

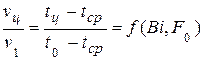, (4.31)

где 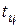– температура в центре пластины, цилиндра, шара.

Количество теплоты, которое отдаёт (или воспринимает) пластина за время τ, должно равняться изменению её внутренней энергии за период полного её охлаждения (нагревания).

Начальная внутренняя энергия пластины, отсчитанная от внутренней энергии при температуре среды, окружающей стенку, как от нуля, равна

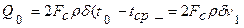(4.32)

При использовании безразмерных комплексов (критериев Bi и F₀) количество теплоты, выделившейся при охлаждении пластины, равно

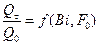(4.33)

или

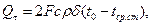(4.34)

где Q_τ – количество теплоты, переданное в окружающую среду за время τ;

t_cp.ст. – средняя температура стенки по истечении периода времени τ.

Зависимости (4.31), (4.32), (4.33) даются в виде таблиц или в виде графиков (рисунки 4.4, 4.5, 4.6, 4.7, 4.8).

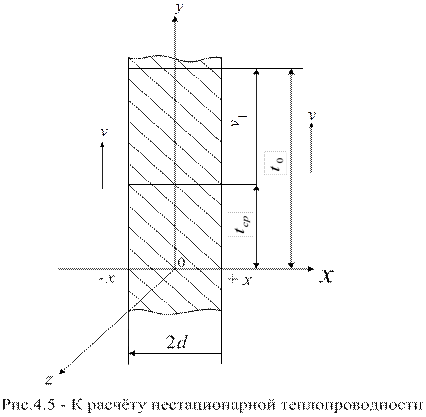
Порядок определения температуры на поверхности тела и в его центре.

Рассмотрим охлаждение плоскопараллельной пластины толщиной 2 δ ( 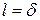). Размер пластины в направлении осей O_y и O_z бесконечно велики. Пластина омывается с обеих сторон жидкостью или газом с постоянной температурой t_cp, причём коэффициент теплопередачи α, для обеих поверхностей имеет одинаковое и постоянное значение.

В начальный момент времени пластина имеет во всех своих точках постоянную температуру t₀, поэтому и избыточная температура v₁=t₀-t_cp будет также постоянной для всех точек тела. Кроме того, заданы коэффициент теплопроводности λ_ст, плотность тела ρ_ст и теплоёмкость его с_ст , величины которых полагаются постоянными.

Порядок определения температуры на поверхности тела и в центре его следующий.

1. Определяют критерий Bi и F₀ по формулам (4.28).

2. По специальным таблицам (табл. 4.3, 4.4, 4.5) определяют относительные (безразмерные) температуры 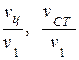и безразмерную теплоту Q_τ/Q₀.

3. Поскольку начальные значения t₁, t_cp и начальная теплота Q₀ известны, то по формулам 4.30, 4.31 и 4.33 определяют значения температур:

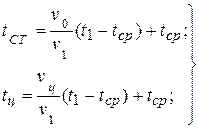(4.35)

и величину тепла Q_τ.

Аналогично определяются температура t_ст, t_ц, Q_τ для бесконечного цилиндра и шара. Однако в качестве характерного размера 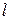в системе уравнений (4.28) принимается радиус цилиндра (шара), т.е.

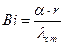и 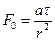(4.36)

Безразмерные температуры и безразмерные величины тепла цилиндра и шара даны в табл. 4.6, 4.7, 4.8.

Пример 4.2. Определить температуру на поверхности и в центре равномерно нагретого до t₁=927°C длинного стального цилиндра диаметром d_ц равным 400 мм через 0,5 часа и через 1,0 час после помещения его на воздухе с температурой 27°C. Коэффициент теплоотдачи от стенки, цилиндра к воздуху α=50 Вт/м²∙К, коэффициент теплопроводимости стали λ_ст=50 Вт/м∙К, плотность стали ρ_ст=7900 кг/м³.

Решение

1. Определим температуры поверхности t_ст и центра t_ц, спустя 0,5 ч после пребывания цилиндра на воздухе:

а) коэффициент температуропроводимости

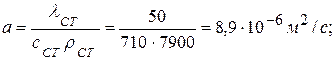
б) критерий Фурье

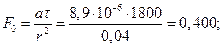
в) критерий Био

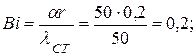
г) По табл. 4.7, 4.6 находим безразмерные температуры при известных критериях Био и Фурье

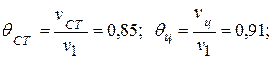
д) температура поверхности цилиндра определяется по формуле (4.35)

;

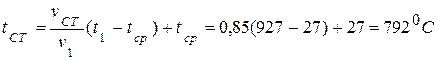е) температура в центре цилиндра

;

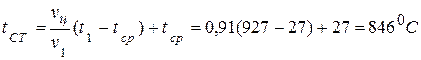ж) потери тепла цилиндра за 0,5 ч по табл. 4.8.

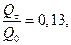т.е. цилиндр потерял 13% от своей начальной внутренней энергии.

2. Определим температуры поверхности t_ст и центра t_ц спустя 1,0 ч после пребывания цилиндра на воздухе:

а) критерий Фурье

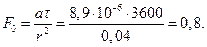
Критерий Био остаётся неизменным.

б) по значениям критериев Bi и F₀ из табл. 4.7 и 4.6 находим безразмерные температуры

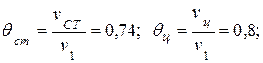
в) температура поверхности цилиндра

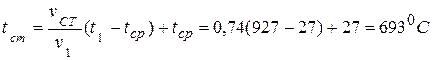
г) температура в центре цилиндра

;

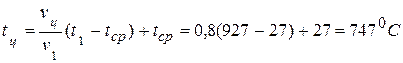д) потери тепла цилиндра за 1 ч. по табл. 4.8

е) 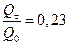, т.е. цилиндр потерял 23% тепла от своей начальной внутренней энергии.

На основании расчётных данных можно построить поле распределения температур по времени и пространству, как показано на рис. 4.6.

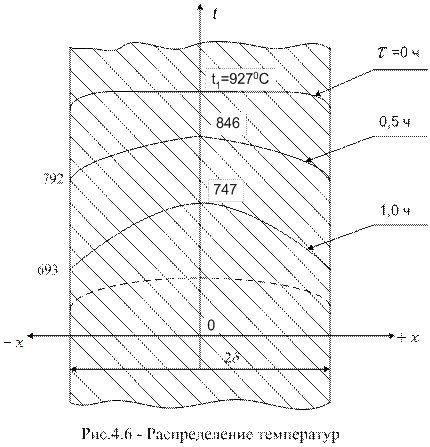
Данная задача может быть решена с использованием графиков (номограмм). На рис. 4.4, 4.5, 4.6 представлены номограммы для определения температуры в телах (пластине, цилиндре, шаре).

Недостатком номограмм, как и таблиц, является то, что они пригодны только для определения температуры в центре тела и на его поверхности.

Рассмотрим задачу, взятую с исходными данными из примера 4.2.

1. При известных значениях критериев Bi=0,2 и F₀=0,4 (для τ=0,5 ч) из номограмм (рис. 4.4, 4.5) получается 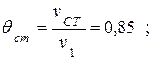и .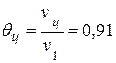

2. Используя формулу 4.35, получим:

а) температуру на поверхности цилиндра

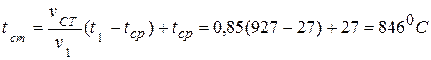
б) температура в центре цилиндра

.

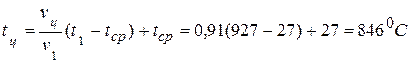3. При известных значениях критериев

Bi=0,2 и F₀=0,8 (τ=1,0 ч) из номограмм (рис. 4.4, 4.5) получаем

.

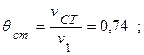
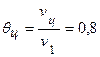Следовательно,

;

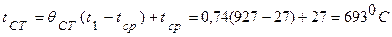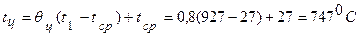
Таким образом, с увеличением времени охлаждения температуры поверхности и центра цилиндра уменьшаются.

Для решения аналогичной задачи при отсутствии таблиц и монограмм используется характеристическое уравнение вида [7]

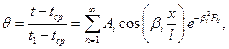(4.37)

или по формулам, приведённым к таблице.

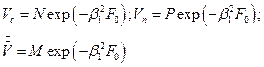
(при B_i<0,1; F₀≥0,3)

где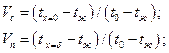

t – температура пластины на расстоянии к от средней плоскости в момент времени τ; считая от начала охлаждения (нагревания)

t₀ – начальная температура тела;

t_ж – постоянная температура жидкости (газа).

4.3 Конвективный теплообмен

4.3.1 Основные понятия теории конвективного теплообмена

Понятие конвективного теплообмена охватывает процесс теплообмена при движении жидкости или газа. При этом процесс переноса тепла осуществляется одновременно конвекцией и теплопроводностью.

Эксперименты и теоретические исследования показали, что конвективный теплообмен определяется многими факторами. Главными из них являются:

- характер и режим движения (вынужденное или свободное движение, ламинарный или турбулентный режим);

- скорость движения теплоносителя;

- физические свойства и состояние теплоносителя (газа или жидкости, передающих тепло стенкам сосудов или трубопроводов);

- форма, состояние и размеры поверхности твердого тела (стенки сосудов, труб);

- направление и величина теплового потока.

Решение задачи конвективного теплообмена сводится к определению теплового потока, идущего от теплоносителя в стенку и обратно.

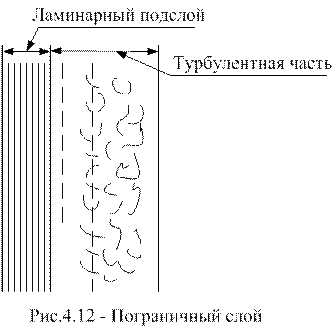
При движении теплоносителя на поверхности стенки возникает пограничный слой, состоящий из двух частей:

а) турбулентной части пограничного слоя – переходной зоны от турбулентного течения к ламинарному;

б) ламинарного слоя (ламинарного подслоя).

В турбулентной части основное количество тепла переносится за счет тепловой конвекции, путем интенсификации перемешивания частиц.

В ламинарной части перенос тепла в направлении нормали к стенке осуществляется в основном теплопроводностью.

Согласно закону сохранения энергии, количество теплоты, отдаваемой единицей поверхности тела окружающей среде в единицу времени вследствие теплоотдачи, должно быть равно теплоте, которая путем теплопроводности подводится к единице поверхности в единицу времени со стороны внутренних частей тела, т.е.

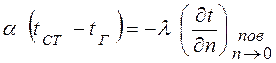(4.23)

или 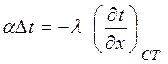- дифференциальное уравнение теплоотдачи.

Для определения теплового потока q необходимо знать температурный градиент 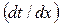_ст, что очень трудно осуществить.

Количество тепла, передаваемого стенке путем конвекции, определяется по формуле Ньютона – Рихмана

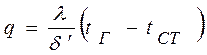, (4.24)

где 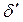- толщина пограничного слоя;

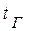- средняя температура в ядре потока газа (жидкости);

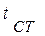- средняя температура у стенки.

Обозначив 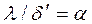- коэффициент теплоотдачи, формулу (4.24) можно выразить в виде

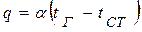(4.25)

В инженерной практике часто используют уравнение Ньютона-Рихмана в виде

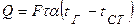, (4.26)

где 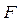- площадь поверхности теплообмена, ;

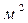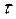- время, с.

Сложность расчета заключается в определении коэффициента 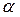. Коэффициент 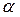определяет интенсивность теплообмена между поверхностью стенки и окружающей средой и численно равен удельному тепловому потоку при температурном напоре, равном 1°С.

Коэффициент 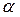зависит от многих факторов, но при решении задач теплоотдачи его в большинстве случаев принимают величиной постоянной.

Для определения коэффициента 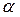используют теоретико-экспериментальный путь (метод).

4.3.2 Понятие о теории подобия

В исследовании теплообмена, как и в других науках, не все явления можно выразить аналитически, т.к. в большинстве случаев система дифференциальных уравнений, описывающая явление, включает неинтегрируемые дифференциальные уравнения. В этом случае большое значение приобретает эксперимент. Однако при экспериментах возникает необходимость создать модели для того, чтобы удешевить постановку опыта, упростить экспериментальную установку.

Исследование явлений на моделях называется моделированием. Научной базой метода моделирования является теория подобия в сочетании с методами теории размерностей.

Основной задачей моделирования является определение условий, обеспечивающих подобие явлений. Теория подобия указывает, как нужно провести эксперимент на модели, чтобы полученные в нем результаты можно было использовать при расчетах явлений, родственных изучаемому на натуре. Таким образом, теория подобия, по существу, является теорией организации и проведения эксперимента.

В основе теории подобия лежит понятие о подобных явлениях.

Различают геометрическое и физическое подобие. Обязательной предпосылкой подобия физических величин является геометрическое подобие.

Геометрическое подобие – это подобие геометрических фигур. Суть геометрического подобия заключается в том, что в геометрически подобных фигурах соответствующие углы равны и сходственные стороны пропорциональны (рис.4.13).

Б

а) натура Б¢ б) модель

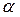
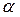
А С А¢ С¢

Рис. 4.13 - Подобные фигуры

Иными словами, геометрическое подобие наблюдается между 2-мя фигурами: натура (АВС) и модель (А¢ B¢ С¢), где линейные размеры и 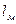, площади S_н и S_м и объемы W_н и W_м находятся в соотношениях

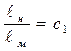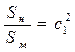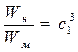; ; (4.27)

где 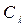- линейный масштаб моделирования; значки «н» и «м» означают «натура» и «модель».

Физическое подобие – это подобие физических явлений. Например, подобие движения потока жидкости, подобие тепловых процессов и т.д.

В физически подобных явлениях однородные величины, имеющие одинаковый физический смысл и размерность, характеризующее явление, подобны. Они сопоставляются в сходственных точках пространства в сходственные моменты времени.

Сходственными точками пространства называются такие точки, координаты которых связаны отношениями геометрического подобия (4.27), асходственными моментами времени называются такие моменты, которые имеют общее начало отчета и связаны условиями временного подобия.

В основе теории подобия лежат три теоремы.

1-я теорема подобия.

Подобные явления имеют одинаковые по величине критерия подобия. Таким образом, первая теорема подобия устанавливает связь между константами подобия и позволяет вывести уравнения для критериев подобия. Теорема указывает, что при выполнении опытов необходимо и достаточно измерять лишь те величины, которые входят в критерии подобия изучаемого явления.

Эта теорема была высказана еще И.Ньютоном в 1686г.

2-я – теорема подобия.

Любая зависимость между переменными, характеризующими явление, может быть представлена в виде зависимости между критериями подобия.

Эта теорема утверждает, что операция интегрирования дифференциальных уравнений, описывающих явление, не изменяет вида критериев подобия. Например, уравнение скорости частицы жидкости v=dt/dt и уравнение после интегрирования, если за период времени t скорость сохраняет свое значение, 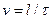дают возможность получить один и тот же критерий гомохронности (Н₀)

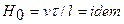
3-я теорема подобия. Необходимым и достаточным условием физического подобия является подобие условий однозначности при равенстве критериев, составленных из условий однозначности. Условиями однозначности являются:

- геометрическое подобие систем;

- одинаковость дифференциальных уравнений, описывающих данное явление.

- существование и единственность решения уравнений при заданных граничных условиях;

- известность численных значений коэффициентов и физических параметров, входящих в дифференциальное уравнение.

Совокупность всех перечисленных условий называется условиями однозначности явления.

Теория подобия дает общие методологические указания, как поступать в каждом отдельном случае при анализе уравнений, описывающих явление, устанавливает пути для правильной постановки опыта и дает указания по обработке полученных результатов.

Критериев подобия очень много и их можно получить для любого явления. Например:

а) Критерии подобия движения жидкости (газа) – критерий Эйлера, Е_u.

Запишем для двух подобных явлений уравнение движения газа в форме Эйлера:

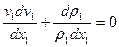
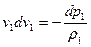; (4.28)

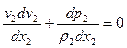
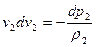(4.29)

Выразим параметры первого явления через параметры второго. В этомслучае

; ; ; .

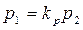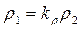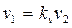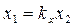С учетом того, что коэффициенты подобия 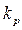, , 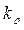, 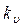и являются постоянными величинами, можно записать, подставив параметры (4.28) в выражение (4.29)

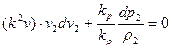. (4.30)

Из условия (4.29) следует, что для выполнения (4.30) необходимо, чтобы

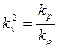, (4.31)

откуда

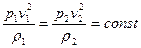(4.32)

или 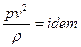(4.33)

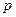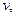
Очевидно, что на основе выражения (4.32) можно сделать вывод о том, что в двух подобных явлениях комплекс параметров , 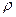один и тот же, что соответствует выражению (4.33).(«idem» - означает одно и то же).

Подобные безразмерные комплексы называют критериями подобия. Их называют, как правило, именами выдающихся ученых. Так, критерий 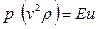- критерий Эйлера. Он характеризует соотношение между силами инерции и давлением газа.

Гидродинамические условия движения потока, соотношение сил инерции и сил трения характеризуются критерием Рейнольдса вида

,

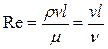где 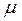- коэффициент динамической вязкости, ;

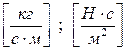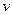- скорость потока;

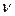- коэффициент кинематической вязкости, .

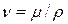б) Критерии теплового подобия

Тепловое подобие – это подобие температурных полей и тепловых потоков.

В технике широкое распространение получил метод теплового подобия. Благодаря применению этого метода расчет теплообмена в некоторых конкретных условиях значительно упрощается в связи с возможностью использовать для расчета экспериментальных зависимостей, полученных в других условиях. Для этого необходимо соблюдать равенство соответствующих критериев в данных условиях и в условиях эксперимента.

Конвективный теплообмен характеризуется пятью критериями подобия:

1. Критерий Нуссельта Nu

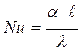(4.33)

где 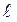- характерный линейный размер;

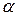- коэффициент теплоотдачи;

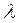- теплопроводность теплоносителя.

Критерий Нуссельта представляет собой безразмерный критерий теплоотдачи, характеризующий условия теплообмена на границе между стенкой и газом, т.е. характеризует интенсивность теплообмена.

2. Критерий Рейнольдса Re

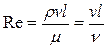; (4.34)

характеризует соотношение, сил инерции и сил вязкости в потоке (или сил трения)

3. Критерий Пекле Pe

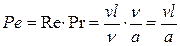? (4.35)

где 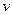- скорость потока;

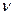- коэффициент кинематической вязкости;

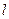- характерный размер;

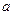– физический параметр или коэффициент температуропроводности, который характеризует скорость изменения температуры.

,

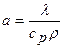где с_p - удельная изобарная теплоемкость теплоносителя;

Если в критерий Пекле вместо коэффициента 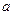подставить его значение 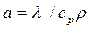и помножить числитель и знаменатель на избыточную температуру 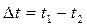, т.е

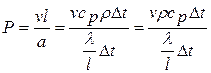, (4.36)

числитель критерия 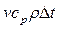- характеризует теплоту, переносимуюконвекцией, а знаменатель 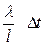- теплоту, переносимую теплопроводностью. Таким образом, чем больше величина критерия Pе, тем большая доля тепла, переносимая в теплоносителе за счет конвекции по сравнению с долей тепла, переносимой теплопроводностью.

4. Критерий Прандтля P_r

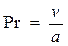; или 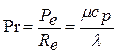(4.37)

Критерий Прандтля характеризует физические свойства теплоносителя.

Для жидкостей критерий P_r сильно зависит от температуры (Pr=1...2500).

Для газов критерий Pr не зависит от температуры (P=0,67...1,0).

5. Критерий Фурье (F₀)

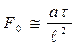(4.38)

где 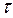- время;

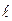- характерный параметр (например, толщина стенки );

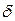Критерий Фурье характеризует подобие конвективного теплообмена при нестационарных процессах (в него входит время ).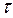

С учетом выше изложенных теорем подобия, рассмотрим исследуемое явление, которое характеризуется n – критериями подобия, полученными из уравнения, описывающее явление и условия однозначности: К_1, К_2, К₃ ...К_n.

Если в критерий К₁ входит 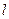интересующий нас параметр, то согласно 2 - ой теоремы подобия можно записать

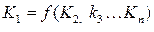/ (4.39)

Такое уравнение называют критериальным.

В явном виде критериальное уравнение записывается в виде произведения критериев в некоторой степени.

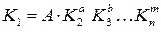(4.40)

где А – коэффициент пропорциональности;

a, b... m – показатели степени, определяемые опытным путем.

Так для расчета конвективного теплообмена используется зависимость вида

.

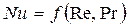Наиболее распространенной формулой, справедливой для конвективного теплообмена при течении жидкости (газа) с невысокой скоростью по каналу любого поперечного сечения, является формула академика М.А. Михеева, полученная на основе отработки большого числа опытов, которая имеет следующий вид:

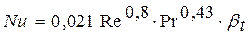. (4.41)

Так температура поперек пограничного слоя изменяется от температуры в ядре потока t_я до температуры его у стенки t_f , а физические параметры входящие в критерии подобия, являются функцией температуры, то для правильного использования формулы (4.41) всегда необходимо указывать, при какой температуре должны определяться критерии подобия. В данной формуле каждый критерий подобия снабжен индексом f.

Коэффициент 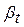называется коэффициентом неизотермичности и определяется следующим выражением

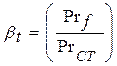, (4.42)

где 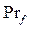- число Прандтля для жидкости (газа), вычисленное при температуре ядра потока;

Рr_ст - то же число, но вычисленное при температуре стенки.

Наличие этого коэффициента в формуле (4.41) объясняется следующим обстоятельством. Как показывает опыт, при одинаковых условиях теплообмена между стенкой и газом и при одной и той же разности температур t_f - t_ст(или t_ст - t_f) величина теплового потока будет различна в зависимости от его направления: от жидкости в стенку и наоборот.

Без коэффициента 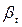формула (4.41) дала бы для коэффициента теплоотдачи 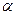один и тот же результат, что не согласуется с опытом.

Для капельных жидкостей формула (4.41) справедлива только при отсутствии кипения жидкостей.

В развернутой формуле выражение (4.41) примет вид:

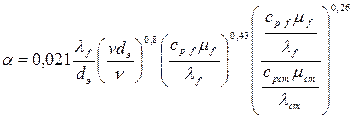. (4.43)

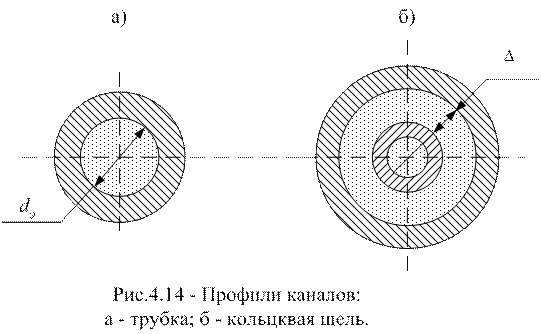
Определяющим геометрическим параметром, характеризующим геометрическое подобие явлений, в данной формуле служит эквивалентный диаметр d_э Он определяется по формуле

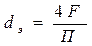, (4.44)

где F – площадь поперечного сечения канала;

П – смоченный периметр.

Для трубы диаметр d_э равен диаметру трубы; для кольцевой щели - 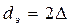(рис. 4.11).

Выражения (4.41) и (4.43) используются для расчета каналов всевозможных форм при критерии Рейнольдса от 10⁴ до 5·10⁶ и P_r =0,6 ... 2500 как для случая нагрева, так и для случая охлаждения жидкости (газа). Для газов 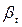=1 и 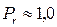формула (4.41) примет следующий простой вид

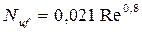(4.45)

Однако эта формула непригодна для расчета при околозвуковых и сверхзвуковых скоростях потока газа.

Расчетное выражение (4.41) или (4.43) справедливо для длинных труб, у которых отношение длины к диаметру 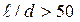. Для коротких труб значение коэффициента 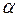, полученное по формуле (4.41), необходимо умножить на поправочный коэффициент 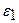, который берется из таблицы 4.11.

Для расчета коэффициента 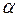от газов к стенке в случае больших дозвуковых скоростей газов также применяется формула Илюхина Н.А. и Гухмана А.А.

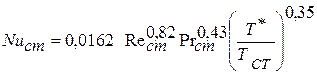(4.46)

где 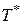- температура торможения в газовом потоке;

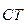« » - характеристики газа у поверхности стенки за исключением плотности газов при термодинамической температуре 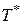газа.

4.4 Лучистый теплообмен

4.4.1 Законы теплового излучения

Тепловое излучение представляет собой вид электромагнитного излучения с длиной волны 0,8 мкм до 0,8 мм

Для лучистых потоков можно записать

Е= ,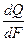

где Е – плотность потока излучения, Вт/м² (или излучательная способность тела)

Q – поток теплового излучения, Вт;

F – площадь поверхности излучения, м².

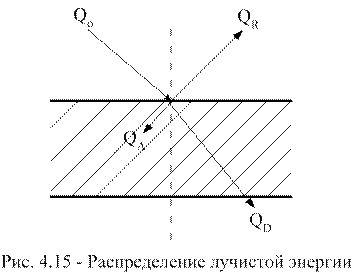
В соответствии с законом сохранения энергии, как показано на рисунке 4.6 тепловой поток распределяется

Q₀=Q_A+Q_R+Q_D,

или 1=A+R+D.

где А=Q_A/Q_o - (коэффициент поглощения) поглощательная способность тел;

R=Q_R/Q_o – (коэффициент отращения) отражательная способность тела;

D=Q_D/Q_o – (коэффициент проницаемости) пропускательная способность тела.

Если А=1, то тело называется абсолютно черным (АЧТ);

Если R=1, то тело называется абсолютно белым;

Если D=1, то тело называется абсолютно прозрачным.

У сажи ламповой А=0,945; у серебра полированного R=0,98; у одноатомных газов D=0,98…0,99.

Рассмотрим основные законы излучения.

Связь между излучательной (Е) и поглощательной способностью тела (А) устанавливается законом Кирхгофа.

Этот закон утверждает, что отношение лучеиспускательной способности к поглощательной для всех тел одинаково и зависит только от температуры

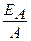=f(Т)

Если отнести это уравнение к абсолютно черному телу (которое будем отмечать индексом 0), то в связи с А₀=1 получится

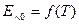
Таким образом, эта универсальная функция есть не что иное, как лучеиспускательная способность АЧТ.

Соответственно этому закон Кирхгофа будет изложен так: для любого тела отношение его лучеиспускательной способности к поглощательной способности равно лучеиспускательной способности абсолютно черного тела при той же температуре

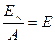или

Дата добавления: 2014-10-10; просмотров: 1084; Нарушение авторских прав

Мы поможем в написании ваших работ!