Лекция 23. Теплообмен при изменении агрегатного состояния вещества

Критерии подобия — это безразмерные комплексы, составленные из разноименных физических величин, описывающих данное явление и связанных взаимными уравнениями.

Критерии подобия одинаковы для подобных явлений.

Рассмотрим, как выводится один из критериев подобия на примере исследования передачи теплоты от стенки в омывающей ее жидкости с турбулентным режимом течения. Известно при этом, что:

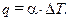(11.3)

Поскольку в ламинарном подслое единственным возможным механизмом передачи теплоты является теплопроводность, то согласно закону Фурье

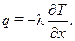(II.4)

Если рассматривать стационарный режим передачи теплоты (т.е. q=const ), то следует приравнять правые части в выра­жениях (11.3) и (11.4):

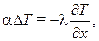
откуда

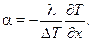(11.5)

Для подобного физического явления можно записать, что

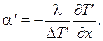(11.6)

Будем считать, что для явлений, описываемых уравнениями (11.5) и (11.6) известны все константы подобия, т.е.

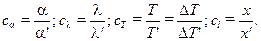(11.7)

Из (11.7) легко определить, что

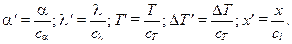(11.8)

Запишем уравнение (11.6) с учетом (11.8) через константы подобия. Получим

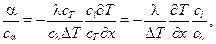
откуда

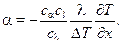(11.9)

Сравнив (11.9) и (11.5), нетрудно получить, что

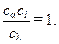
Отсюда следует

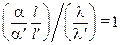
или

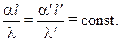
Полученный комплекс (подставив в него размерности 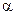и l, убедимся, что он безразмерный) носит название критерия подобия Нуссельта.

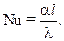(11.10)

Заметим, что в выражении (11.10) l — это характерный размер. Так, в случае омывания пластины жидкостью l — это толщина теплового слоя, в случае течения жидкости в цилиндрической трубе l — диаметр трубы.

Дадим физическое определение критерия подобия.

Критерий Нуссельта характеризует соотношение между интенсивностью теплопроводности в пограничном ламинарном подслое и интенсивностью общей конвекции.

Заметим, что все критерии теплообмена и гидродина-мики имеют определенный физический смысл и, как правило, им присвоены имена ученых, внесших большой вклад в исследование процессов теплообмена и гидродинамики.

Перечислим некоторые наиболее часто встречавшиеся в теории теплообмена и гидродинамики критерии.

Критерий Рейнольдса — характеризует соотношение между силами инерции и силами вязкого трения в жидкости или газе.

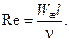
Здесь W_ж — скорость течения жидкости; ν — коэффициент кинематической вязкости жидкости, [ν]=м²/с; l — характерный размер, например, диаметр трубы.

Критерий Рейнольдса служит для определения режима течения жидкости. Так, в случае течения жидкости в трубе при скоростях течения, для которых Re<2300, наблюдается ламинарный режим. При Re>10⁴ устанавливается развитый турбулентный режим.

В случае продольного обтекания жидкостью пластины турбулентный режим наблюдается на таких от нее расстояниях, при которых Re>5∙10⁵.

Переход ламинарного режима течения в турбулентный с ростом критерия Re, который увеличивается, в свою очередь, только за счет роста скорости течения (при неизменных геометрии объекта и рода жидкости), легко объясним. Действительно, при ламинарном режиме течения жидкости силы вязкости должны преобладать над силами инерции и препятствовать ее перемешиванию в продольном направлении. Но как только силы инерции (определяемые скоростью течения) становятся больше сил вязкости, начинают интенсивно развиваться вихревые потоки в жидкости и наступает турбулентный режим.

Критерий Грасгофа характеризует соотношение подъемной вилы, возникающей при наличии сил тяжести в результате теплового расширения жидкости или газа, к силам вязкости

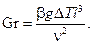(11.12)

Здесь g — ускорение свободного падения; β — температурный коэффициент объемного расширения среды, [β]= 1/K; ΔТ — температурный напор.

Критерий Прандтля характеризует теплофизические свойства вещества. Это соотношение между интенсивностями молекулярного переноса количества движения и переноса теплоты теплопроводностью.

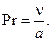(11.13)

Значения критерия Прандтля приводятся в теплофизических справочниках.

В случае нестационарного режима теплопередачи (т.е. неустановившегося во времени, например, при нагреве или охлаждении тел) часто пользуются критерием Фурье Fo

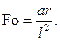(11.14)

и критерием гомохронности Нo;

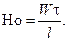(11.15)

Лекция 23. Теплообмен при изменении агрегатного состояния вещества.

Кипение — это процесс парообразования в толще жидкости. Считают, что этот процесс начинается тогда, когда при некотором давлений p_ж температура жидкости достигает температуры насыщенных паров при том же давлении, т. е.

Т_ж=Т_н=Т_s.

Так, для воды при нормальном давлений p_ж=101,325 кПа (p_ж=760 мм рт. ст.) T_s=373 К. Однако чтобы жидкость закипела, ее температура должна несколько превышать T_s. Другими словами, давление пара должно превысить давление окружающей жидкости. В случае отсутствия этого некоторого перегрева жидкости образование пузырей в толще воды становится невозможным.

Рассмотрим условия, при которых может существовать пузырек пара в толще воды (рис. 12.4).

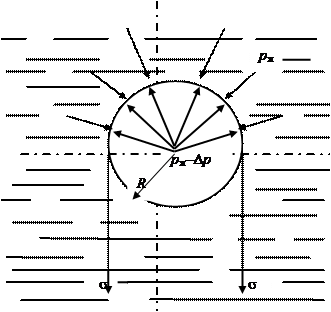
Рис. 12.4 Силы, действующие на сферический паровой пузырь в кипящей жидкости

Будем считать, что на пузырек пара действуют только давление жидкости и силы поверхностного натяжения. Напомним, что поверхностные силы — это силы, под действием которых свободная поверхность жидкости стремится сократиться (это касательные к поверхности силы).

Мысленно разрежем сферический пузырь по диаметру и заменим действие нижней его половины погонной силой поверхностного натяжения, как это показано на рис. 12.4.

Тогда из условия равновесия сил, действующих на поверхность половины пузыря, следует, что

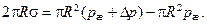
откуда нетрудно определить, что величина превышения давления пара над давлением жидкости определяется следующим образом:

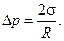
Таким образом, если в жидкости при достижении температуры Т_ж=Т_н+ΔТ будут находиться пузыри газа, для которых 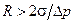, то такие пузыри будут расти. В этом случае давление пара превышает давление жидкости и силы поверхностного натяжения. Пузыри, у которых 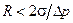, будут сокращаться под действием поверхностных сил. Следовательно, чтобы началось кипение жидкости, ее надо несколько перегреть.

Величина перегрева жидкости, как установлено экспериментально, зависит от таких факторов, как чистота жидкости, ее давление и состояние поверхности.

Жидкость, тщательно очищенную от растворенных в ней газов и различного рода взвешенных в ней частиц при нормальном давлении удавалось нагреть до температуры, на десятки градусов выше табличного значения температуры кипения. Наступавшее, в конце концов, кипение проходило очень бурно, напоминая взрыв.

Однако для того, чтобы жидкость закипела, одного перегрева недостаточно. Пузырьки пара не могут расти из ничего. Для их появления необходимы очаги или зародыши парообразования. К ним относятся растворенные в жидкости газы или взвешенные частицы, а также шероховатости поверхности, через которые к жидкости подводится тепло. Чем больше таких очагов, тем меньше требуется перегрев жидкости для ее кипения, и наоборот. Наибольшее число таких центров парообразования (микротрещин с парогазовыми пузырьками) находится у стенки. Именно здесь и начинается кипение.

Различают несколько режимов кипения (рис. 12.5), Для удобства на графике значения тепловой нагузки q в зависимости от перегрева поверхности нагрева ΔT будем рассматривать в логарифмической системе координат. Проанализируем так называемую кривую кипения воды (зависимость q=f(DT)), полученную при контролируемой температуре поверхности нагрева.

На участке AB при перегреве теплопередающей стенки примерно до 9 К в воде наблюдается естественная конвекция.

При дальнейшем перегреве (участок BC) начинается при DT=9 K пузырьковое кипение. Зарождающиеся на поверхности пузырьки растут, отрываются от поверхности и всплывают вверх. При этом они интенсивно перемешивают (барботируют) жидкость. За счет этого резко возрастает количество передаваемой через жидкость теплоты (заметим, что сами пузырьки забирают от стенки немного теплоты, но они способствуют ее переносу). При этом режиме q достигает величины порядка 1,2×10³ кВт/м², a α≈15 кВт/м²×К и выше.

Однако начиная со степени перегрева стенки порядка 25–55 К, наступает переходный режим кипения (участок CD), который характеризуется заметным падением величины q (до 25–30 кВт/м²) и α (до 8 кВт/м²∙К) Это обусловлено тем, что при дальнейшем росте перегрева пузырьки начинают сжиматься, образуя большие паровые полости. При этом ухудшается доступ жидкости к стенке. И поскольку воздух обладает плохой по сравнению с. водой приводимостью тепла, то теплопередача резко уменьшается.

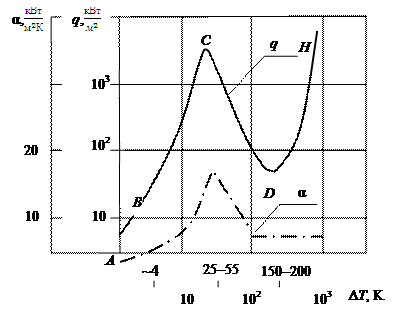Рис. 12.5 Зависимость удельного теплового потока и коэффициента теплоотдачи от степени перегрева поверхности нагрева при кипении воды в случае контролируемой температуры нагревателя

Начиная со значений ΔТ=150–200 К, наступает режим пленочного кипения (участок DH). При этом вся поверхность покрывается паровой пленкой. Эта пленка постоянно пульсирует: периодически пар, накапливаемый под пленкой, отрывается от стенки в виде больших пузырей. Условия теплопередачи не меняются (α=const). Рост же q на этом участке обусловлен только ростом ΔТ.

Режим пленочного кипения самый неблагоприятный при охлаждении нагреваемой поверхности жидкостью. При этом режиме к стенке подводится большое количество тепловой энергии, но жидкости передается энергии при этом значительно меньше, чем при пузырьковом кипении. Это может привести к пережогу стенки.

Поэтому тепловая нагрузка (т.е. количество тепловой энергии, отводимой с единицы поверхности в единицу времени) в точке C называется критической тепловой нагрузкой q_кр.

На рис. 12.6, 12.7 представлены кривые кипения воды полученные при контролируемой тепловой нагрузке. Количество тепла, передаваемое от металлической поверхности к кипящей воде, в этом случае всегда увеличивается с ростом температуры нагревателя.

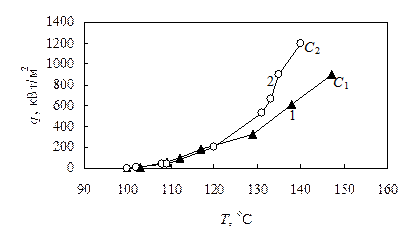Рис. 12.6. Кривая кипения воды, полученная на медном цилиндрическом нагревателе диаметром 100 мкм (1) и вольфрамовом твэле диамером 100 мкм (2) при контролируемой тепловой нагрузке

Материал поверхности нагрева при контролируемой тепловой нагрузке оказывает значительное влияние на форму кривой кипения. Так для цилиндрического нагревателя из меди (диаметр 100 мкм) и вольфрама (диаметр 90 мкм) на рис. 12.6 режим пузырькового кипения при росте тепловой нагрузки заканчивается перегоранием в точках C₁и C₂при низких температурах, составляющих 140 и 147 ^оС, а также критической тепловой нагрузке, равной 895 и 1191 кВт/м².

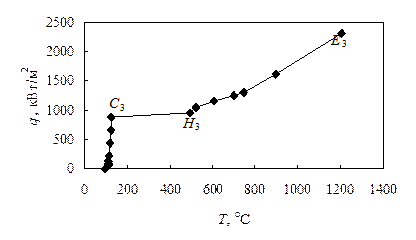Рис. 12.7. Рис. 7. Кривая кипения воды на цилиндрической поверхности нагрева из нихрома диаметром 150 мкм при контролируемой тепловой нагрузке.

Для поверхности нагрева из нихрома диаметром 150 мкм (рис. 12.7) режим пузырькового кипения при малом увеличении плотности теплового потока резко сменяется пленочным (из точки С₃ в H₃), что сопровождается большим увеличением температуры. Расплавление тепловыделяющего элемента в этом случае происходит при температуре 1202 ^оС и тепловой нагрузке 2323 кВт/м² в точке Е₃.

Таким образом, точка разрушения нагревательного элемента не всегда соответствует кризису кипения. Для этого необходимо знать температуру поверхности нагрева. В точках С₁ и С₂, приходящейся на максимум кривой кипения, происходит локальный пережог в целом «холодного» (Т=140 ^оС) нагревателя из медной и вольфрамовой проволоки (рис. 12.6). Для тепловыделяющих элементов из нихрома в точке Е₃ происходит расплавление в целом «горячего» (при температуре, близкой к температуре плавления металла Т=1202 ^оС) нагревателя (рис. 12.7).

Для атмосферного давления при контролируемой тепловой нагрузке существует некоторое кипения критическое (максимальное) значение тепловой нагрузки q_крдля кривой кипения. Абсолютная величина q_кр для всех размеров и материалов тепловыделяющего элемента определении экспериментально и приходится на интервал 779–1541 кВт/м². Этим значениям критической тепловой нагрузки соответствует температурный промежуток 124–152 ^оС.

Тепловая нагрузка, получаемая при пережоге, зависит от материала цилиндрического нагревателя при насыщенном и ненасыщенном кипении. Особенно эта зависимость выражена при ненасыщенном кипении. Опыты показали, что для цилиндрических нагревателей из меди и вольфрама критическая тепловая нагрузка совпадает с тепловой нагрузкой при пережоге. Для поверхностей нагрева из константана, манганина, нихрома критическую тепловую нагрузку необходимо отличать от тепловой нагрузки при пережоге, эти величины не совпадают. При проведении экспериментов по кризису кипения должна всегда определяться температура поверхности нагрева во избежание ошибочной фиксации критической тепловой нагрузки.

Барботаж — прохождение пузырьков газа через жидкость. При барботаже газа через жидкость во время отрыва пузырьки деформируются. Скорость подъема пузырьков W при барботаже для деформированных пузырьков остается постоянной и независимой от размера пузыря. Найдено, что данные для 16 жидкостей могут быть описаны с точностью до 3% следующей формулой:

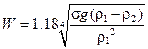. (12.9)

Процесс квазистатического образования пузырька завершается его отрывом под действием гравитации. Можно ожидать, что скорость подъема парового пузыря вблизи нагретой поверхности будет приблизительно равной величине, рассчитанной по уравнению (12.9).

Кружилин Г. Н. исследовал движение газа через слой жидкости в паровых котлах. Пар в виде отдельных пузырьков и струй проходит через слой воды и, разрывая поверхность испарения, поступает в паровой объем барабана котла. При этом оторванные капли жидкости поднимаются над поверхностью испарения или падают вниз обратно, или попадают в паропровод. Для теоретического анализа данной задачи автор применил метод размерностей. Оказалось, что влажность газа

.

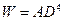Здесь D — напряжение парового объема при барботаже, м³/(м³∙с). Т.е. это объем газа, проходящего через единицу объема жидкости в единицу времени.

Найдено, что в данном случае наиболее существенным является критерий

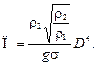
(12.10)

Здесь ρ₁ — плотность жидкости; ρ₂ — плотность пара; σ — поверхностное натяжение жидкости; g — ускорение свободного падения.

Напряжение парового объема D напрямую связано со скоростью пара W, величина П имеет некоторое постоянное значение, поэтому критерий (12.10) можно переписать в следующем виде:

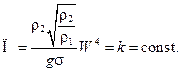(12.11)

Скорость движения паровой фазы выразим из уравнения (12.11):

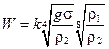. (12.12)

Соотношение (12.12), полученное для скорости движения паровой фазы при барботаже, можно применить к исследованию кипения. Будем считать, что механизм явлений барботажа и кипения аналогичен, тогда запишем подобно уравнению (12.12):

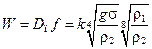. (12.13)

Здесь k=1, W — скорость движения паровой фазы от поверхности нагрева при кипении жидкости; D_п — диаметр парового пузырька; f — частота отрыва паровых пузырей от поверхности нагрева. Для воды при насыщенном кипении при одной атмосфере D_пf =85 мм/с.

Подобие процессов барботажа и кипения применим для описания критической тепловой нагрузки.

Изменение режимов потока при барботаже газа через слой жидкости приводит к следующему явлению. Оказалось, что существует некоторая предельная скорость газа, выше которой струи газа перестают двигаться устойчиво в жидкости. Этот верхний предел называют точкой «погружения» или «затопления». Для данного процесса величина скорости «затопления» определяется как скоростью газа, движущегося от поверхности, так и скоростью жидкости, направляющейся к поверхности. Если нам задана любая скорость газа, то имеется вполне определенная скорость жидкости, выше которой заполненная струя газа будет затопляться.

Механизм явления затопления (захлебывания) при барботаже можно описать следующим образом. Оно происходит в любом устройстве, в котором одна жидкость протекает прерывисто сквозь несмешивающуюся вторую. Дисперсная фаза, когда проходит сквозь непрерывную фазу, имеет меньшую скорость, чем на входе. Скорости сред, текущих навстречу друг другу независимы, поэтому при быстром их синхронном увеличении происходит затопление. Если оно происходит, то возможен один из двух случаев. Первый — прохождение непрерывной фазы задерживается, а дискретная фаза дает задний ход, второй — небольшая задержка в движении любой из сред становится достаточной, чтобы другая заполнила имеющийся в сосуде объем, при этом одна из фаз выливается более или менее сильно из аппарата.

Таким образом, затопление при барботаже происходит, когда встречные потоки жидкости и газа достигают таких скоростей, при которых жидкость и газ начинают конкурировать за свободный объем. Фотографическое исследование кипения показало, что при околокритических тепловых нагрузках от поверхности нагрева движутся струи пара, а жидкость течет в противоположном направлении — к поверхности нагрева. Кризис кипения наступает, если на теплообменной поверхности образуется больше пара по сравнению с тем его количеством, которое могут перенести устойчивые паровые струи.

Кризис кипения — это гидродинамическое явление, которое можно трактовать аналогично явлению затопления. Критическая тепловая нагрузка достигается, когда скорость паровой фазы примет максимальное (критическое) значение. Жидкость будет отброшена от поверхности нагрева, т.е. произойдет отжим жидкости паром.

Г. Н. Кружилин при рассмотрении задачи о влажности пара при барботаже в паровых котлах сделал вывод, что по уравнению (12.10) можно найти зависимость допустимой (критической) нагрузки парового объема от давления в случае прохода пара через свободный объем. В условиях захлебывания при барботаже, которые соответствуют кризису кипения, влажность пара достигает вполне определенного (критического) значения, и поэтому выражение (12.11) можно переписать в виде:

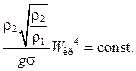(12.14)

Так получается важная в теории кризиса кипения «формула четвертой степени» для скорости движения паровой фазы.

Исходя из рассмотрения развития процессов кипения и барботажа, механизмы кризиса кипения и захлебывания при барботаже одинаковы. Тогда из уравнения (12.14) можно получить выражение для скорости движения паровой фазы:

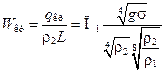. (12.15)

Здесь L – теплота парообразования. Для критической тепловой нагрузки выражение (10) можно переписать:

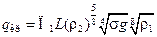. (12.16)

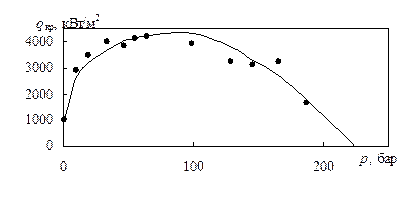Рис. 12.7 Критическая тепловая нагрузка q_кр при насыщенном кипении и воды в зависимости от давления p; кривые — расчет по (12.16); точки — экспериментальные данные Казаковой

На рис. 12.8 для сравнения представлены результаты расчета критической тепловой нагрузки q_кр по формуле (12.16) и экспериментальные данные, полученные при кипении воды в широком диапазоне давлений.

Постоянная П₁ оказалась равной 0.2–0.3. Видно, что согласование расчетных данных с экспериментом удовлетворительное в широком диапазоне давлений. Использование аналогии процессов барботажа и кипения при описании их характеристик является обоснованным.

Применение метода аналогии к процессам барботажа и кипения позволяет получить теоретическое соотношение для критической тепловой нагрузки в широком интервале давлений для различных органических жидкостей и воды.

Дата добавления: 2014-08-04; просмотров: 915; Нарушение авторских прав

Мы поможем в написании ваших работ!