
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ЛОГАРИФМ И ЕГО СВОЙСТВА
1. loga1 = 0
2. logaa = 1
3. 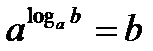 - основное логарифмическое тождество
- основное логарифмическое тождество
4. loga (xy) = logax + logay
5. loga ( 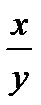 ) = logax - logay
) = logax - logay
6. loga xp = p logax
7. 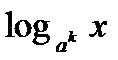 =
= 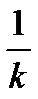 logax
logax
8. logab = 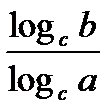
9. logab = 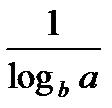
10. log10 x = lg x, loge x = ln x
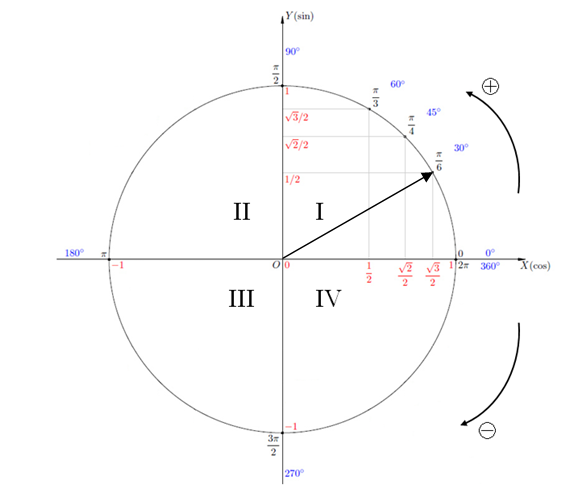
ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
| 00 | 300 | 450 | 600 | 900 | 1800 | 2700 | 3600 | |
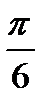
| 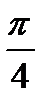
| 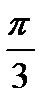
| 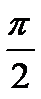
| π | 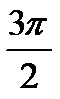
| 2π | ||
| sin x | 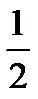
| 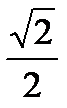
| 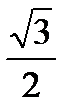
| -1 | ||||
| cos x | 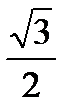
| 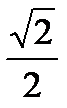
| 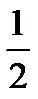
| -1 | ||||
| tg x | 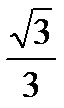
| 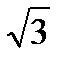
| - | - | ||||
| ctg x | - | 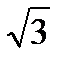
| 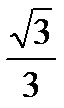
| - | - |
ЧЕТНОСТЬ-НЕЧЕТНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
sin(- x) = - sin x
cos(- x) = cos x
tg(- x) = - tg x
ctg(- x) = - ctg x
ЗНАКИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
| х |
| у |
| х |
| х |
| sinx |
| cosx |
| tgx, ctgx |
| + |
| + |
| + |
| + |
| + |
| + |
ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ
I группа. Соотношения между тригонометрическими функциями одного аргумента:
1) 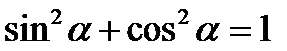
2) 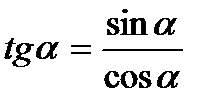
3) 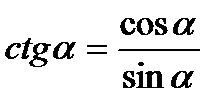
4) 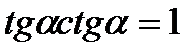
5) 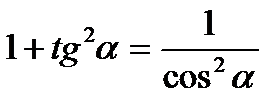
6) 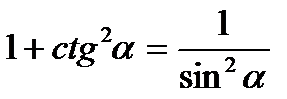
II группа. Формулы двойного аргумента:
1) 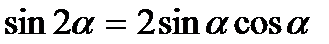 2)
2) 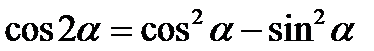 3)
3) 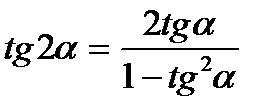
| III группа. Формулы понижения степени:
1) 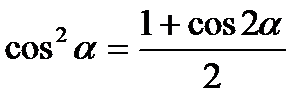 2)
2) 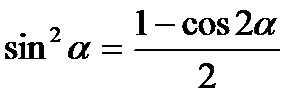
|
IV группа. Формулы сложения:
1) 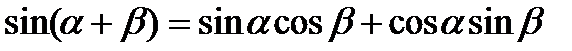
2) 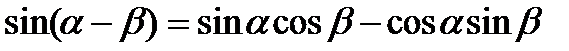
3) 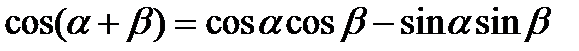
4) 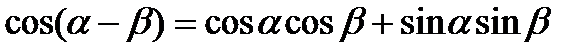
5) 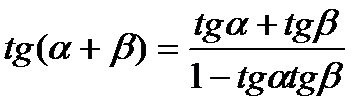 7) ctg
7) ctg 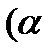 +
+ 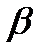 ) =
) = 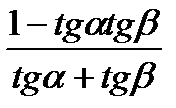
6) 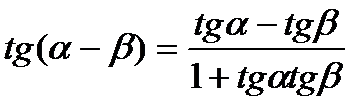 8) ctg (
8) ctg ( 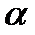 -
- 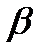 ) =
) = 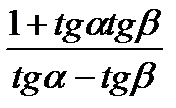
V группа. Формулы преобразования суммы или разности тригонометрических функций в произведение:
1) 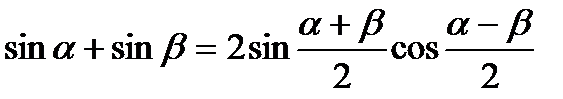 2)
2) 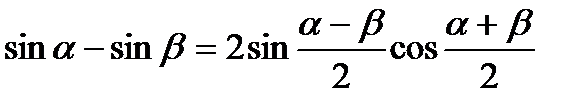 3)
3) 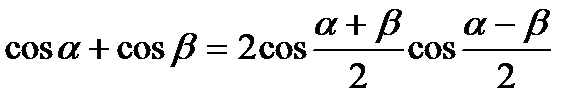 4)
4) 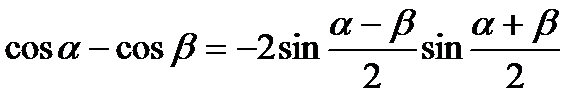
| 5) tg 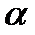 + tg + tg 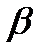 = = 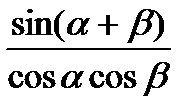 6) tg
6) tg 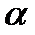 - tg - tg 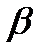 = = 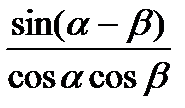 7) ctg
7) ctg 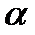 + ctg + ctg 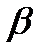 = = 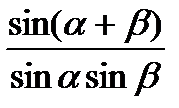 8) ctg
8) ctg 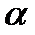 - ctg - ctg 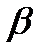 = = 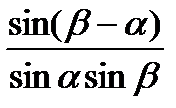
|
VI группа. Формулы преобразования произведений тригонометрических функций в сумму и разность:
1) 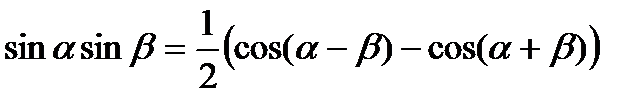
2) 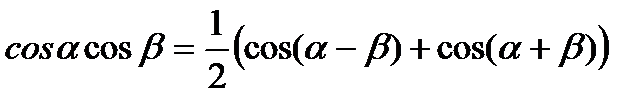
3) 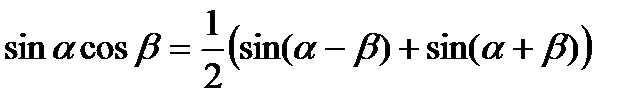
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
arcsin(- x) = - arcsin x
arccos(- x) = π - arccos x
arctg(- x) = - arctg x
arcctg(- x) = π - arcctg x
РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
| sin x = a | sin x = a, а>1 или а<1 | Уравнение корней не имеет | n 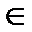 Z Z
|
| sin x = -1 | х = 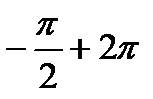 n n
| ||
| sin x = 0 | х = 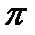 n n
| ||
| sin x = 1 | х = 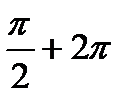 n n
| ||
| sin x = a, -1<а<1 | х = 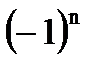 arcsin a + arcsin a + 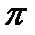 n n
|
| cos x = a | cos x = a, а>1 или а<1 | Уравнение корней не имеет | n 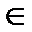 Z Z
|
| cos x = -1 | х = 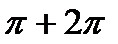 n n
| ||
| cos x = 0 | х = 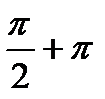 n n
| ||
| cos x = 1 | х = 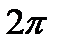 n n
| ||
| cos x = a, -1<а<1 | х = 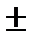 arccos a + arccos a + 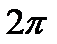 n n
|
| tg x = a | tg x = 0 | х = 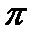 n n
| n 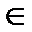 Z Z
|
| tg x = a | х = arctg a + 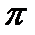 n n
|
| сtg x = a | ctg x = 0 | х = 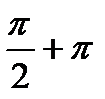 n n
| n 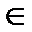 Z Z
|
| ctg x = a | х = arcctg a + 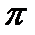 n n
|
| <== предыдущая страница | | | следующая страница ==> |
| ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ. Цель: формирование умения определять принадлежность чисел к множествам N, Z, Q, выполнять действия с десятичными и обыкновенными дробями | | |
Дата добавления: 2014-10-14; просмотров: 407; Нарушение авторских прав

Мы поможем в написании ваших работ!