
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ. Цель: формирование умения определять принадлежность чисел к множествам N, Z, Q, выполнять действия с десятичными и обыкновенными дробями
Раздел 1. АЛГЕБРА И НАЧАЛА АНАЛИЗА
Тема 1.1. Развитие понятия о числе
Задание 1. Множества N, Z, Q. Действия с обыкновенными и десятичными дробями. – 2 ч.
Цель: формирование умения определять принадлежность чисел к множествам N, Z, Q, выполнять действия с десятичными и обыкновенными дробями.
Задание для самостоятельной внеаудиторной работы:
& 1.1. Разберите, какие числа входят во множества натуральных, целых, рациональных чисел. В виде каких десятичных дробей представимы рациональные числа? Вспомните, как выполнить сложение, вычитание, умножение и деление обыкновенных дробей.
Основные сведения из теории:
1.2. Закончите определения:
а) Множество чисел, возникших в результате счёта, называют … и обозначают …
б) Множество, включающее натуральные числа, противоположные им числа и число 0, называют … и обозначают …
в) Множество чисел вида 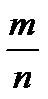 , где
, где 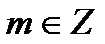 ,
, 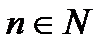 , называют … и обозначают …
, называют … и обозначают …
1.3. Заполните пропуски:
Любое рациональное число может быть представлено либо в виде … десятичной дроби, либо в виде … десятичной … дроби.
Примеры и упражнения:
?1.4. Внесите числа в соответствующие ячейки таблицы:
1; -5; 6,7; 0; 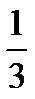 ; 0,(3); 1,23456…; -3,45(6).
; 0,(3); 1,23456…; -3,45(6).
| Числовые множества | N | Z | Q |
| Числа |
?1.5. Переведите:
а) десятичную дробь в обыкновенную: 0,2; 1,75; 4,5.
б) обыкновенную дробь в десятичную: 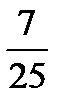 ;
; 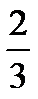 ;
; 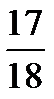 .
.
C1.6.Выполните действия:
а) 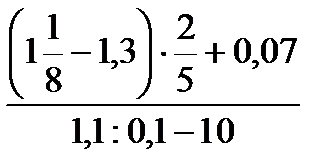 ; б)
; б) 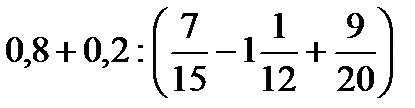 ; в)
; в) 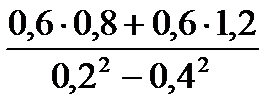 ; г)
; г) 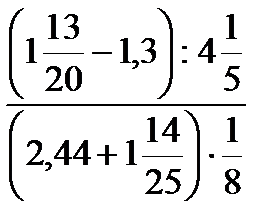 ;
;
д) 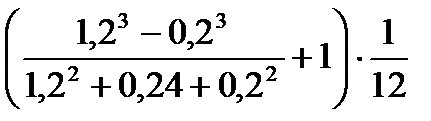 .
.
Выполнив задание 1.6 и заменив получившиеся ответы буквами из таблицы, Вы узнаете фамилию величайшего математика, единственного удостоившегося титула «Короля математиков».
Фамилия короля математиков:
| а) | б) | в) | г) | д) |
Карта ответов:
| А | В | Г | К | Н | О | Р | С | Т | У | Я |
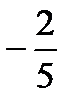
| -1 | -0,5 | 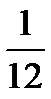
| 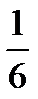
| 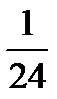
| -10 | 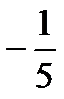
|
 Этот человек говорил про себя, что он «умел считать раньше, чем говорить». Самая ранняя математическая легенда о нем утверждает, что в возрасте трех лет он следил за расчетами отца с каменщиками и неожиданно поправил его, причем оказался прав.
Этот человек говорил про себя, что он «умел считать раньше, чем говорить». Самая ранняя математическая легенда о нем утверждает, что в возрасте трех лет он следил за расчетами отца с каменщиками и неожиданно поправил его, причем оказался прав.
| король математиков |
?1.7. Произведите указанные действия:
а) 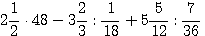 ; б)
; б) 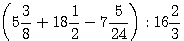 ;
;
в) 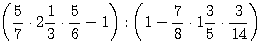 ; г)
; г) 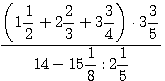 .
.
¶ 1.8. Произведите указанные действия:
а) 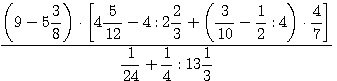 ; б)
; б) 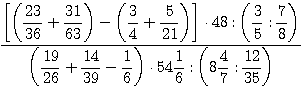 .
.
i1.9. Пройдите тесты на действия с дробями:
· http://reshuege.ru/test?theme=55&ttest=true;
· http://321start.ru/demo/demo.php;
· http://www.berdov.com/docs/fraction/.
Список литературы:
1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2010.- 395 с. - Глава 1, §1, п. 1 - 10, стр. 8 – 13.
Раздел 1. АЛГЕБРА И НАЧАЛА АНАЛИЗА
Тема 1.1. Развитие понятия о числе
Задание 2. Множества I, R, C. Действия над комплексными числами в алгебраической форме. – 2 ч.
Цель: формирование умения определять принадлежность чисел к множествам I, R, C, выполнять операции с комплексными числами в алгебраической форме.
Задание для самостоятельной внеаудиторной работы:
& 2.1. Разберите, какие числа входят во множество иррациональных чисел. Какие числа образуют множество действительных чисел? Что называют мнимой единицей? Какой вид имеет алгебраическая форма комплексного числа? Какова геометрическая интерпретация комплексных чисел? Разберите, как выполнить сложение, вычитание, умножение и деление комплексных чисел в алгебраической форме.
Основные сведения из теории:
2.2. Заполните пропуски:
а) Множество всех … называют множеством иррациональных чисел и обозначают …
б) Объединение множества рациональных и иррациональных чисел называют … и обозначают …
в) Множество чисел вида …. называют множеством комплексных чисел и обозначают …
2.3. Закончите определения:
а) Число, квадрат которого равен …, называют мнимой единицей и обозначают …
б) Алгебраическая форма комплексного числа имеет вид …, где а - …, b - …
в) Комплексное число … можно изобразить в виде … с координатами …
г) Два комплексных числа называются взаимно сопряжёнными, если …
Примеры и упражнения:
?2.4. Внесите числа в соответствующие ячейки таблицы:
-121; 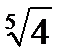 ; 5,2; 3i; 7;
; 5,2; 3i; 7; 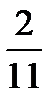 ; 1,(23); π; 0;
; 1,(23); π; 0; 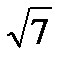 ; 3,243546…; 1-5i.
; 3,243546…; 1-5i.
| Числовые множества | N | Z | Q | I | C |
| Числа |
?2.5. Заполните таблицу по образцу:
| Комплексное число | действительная часть | коэффициент при мнимой части | сопряжённое число |
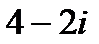
| -2 | 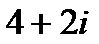
| |
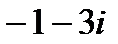
| |||
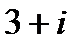
| |||
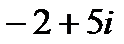
| |||
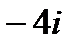
|
?2.6. Используя таблицу 2.5, постройте на комплексной плоскости следующие числа:
а) 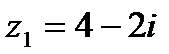 ; б)
; б) 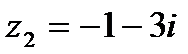 ; в)
; в) 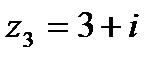 ; г)
; г) 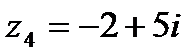 ; д)
; д) 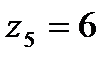 ; е)
; е) 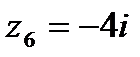 .
.
?2.7. Заданы числа: 1) 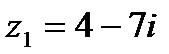 ,
, 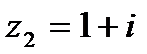 ; 2)
; 2) 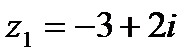 ,
, 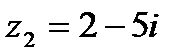 .
.
Для каждой пары 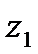 и
и 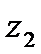 найдите
найдите
а) 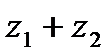 ; б)
; б) 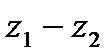 ; в)
; в) 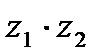 ; г)
; г) 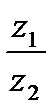 ; д)
; д) 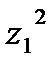 ; е)
; е) 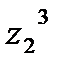 .
.
¶ 2.8. Произведите указанные действия:
а)  ; б)
; б) 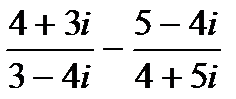 .
.
Список литературы:
1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2010.- 395 с. - Глава 1, §1, п. 11, 12, 15 - 20, стр. 13 – 15, 17 - 24.
Раздел 1. АЛГЕБРА И НАЧАЛА АНАЛИЗА
Тема 1.1. Развитие понятия о числе
Задание 3. Абсолютная и относительная погрешности – 1 ч.
Цель: формирование умения находить абсолютную и относительную погрешности приближённых значений числа.
Задание для самостоятельной внеаудиторной работы:
& 3.1. Разберите, что называют абсолютной и относительной погрешностями приближённых значений числа. Вспомните правила округления чисел.
Основные сведения из теории:
3.2. Заполните пропуски:
а) Модуль разности между … и … значением числа называют абсолютной погрешностью и обозначают …
б) Отношение … к … называют относительной погрешностью и обозначают …
в) Чем относительная погрешность меньше, тем … выше.
3.3. Заполните таблицу:
| Абсолютная погрешность | Относительная погрешность | |
| Формула для расчёта | ||
| Единицы измерения |
Примеры и упражнения:
?3.4. Внесите величины в соответствующие столбцы таблицы по образцу:
| Точные | Приближённые |
| книга содержит 134 страницы | длина стола 1,25 м |
· толщина книги 25 мм;
· температура воздуха 19° C;
· в самолете 122 пассажира;
· скорость звука в воздухе 322 м/с;
· масса дыни 2 кг 300 г;
· стоимость ручки 3 рубля;
· угол в тетради 50° .
?3.5. Заполните следующую таблицу по образцу:
| № | х0 | округлить до | х | 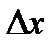
| 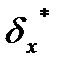
|
| 1,324 | десятых | 1,3 | 0,024 | 1,846 % | |
| 5,289 | сотых | 5,29 | |||
| 999,9 | единиц | ||||
| десятков | |||||
| сотен |
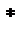 - произведите округление результата с точностью 3 знака после запятой
- произведите округление результата с точностью 3 знака после запятой
?3.6. Решите задачи:
1) Выполняя лабораторную работу по определению плотности железа, ученик получил результат 7,6 г/см3. Вычислите абсолютную и относительную погрешность экспериментального результата (табличное значение плотности железа равно 7,8 г/см3).
2) При измерении расстояния между далеко стоящими объектами первым прибором с точностью до 5 м получено 23,37 км, а при измерении расстояния между близко стоящими объектами вторым прибором с точностью до 0,5 см получено 3 м. Какое измерение по своему качеству лучше?
83.7. Выполните практическое задание:
Цель: Определение плотности твердого тела. Нахождение абсолютной и относительной погрешностей приближенных значений
Ход работы: Выберите брусок в форме параллелепипеда, изготовленный из известного Вам материала.
- Найдите массу бруска, используя динамометр (в лаборатории дисциплины «Физика»).
- Найдите объем бруска, для чего измерьте длину a, ширину b, высоту c бруска. Расчетная формула: V = abc.
- Вычислите плотность бруска по формуле: ρ= m/V.
- Зная, из какого материала сделан брусок, сравните полученное значение плотности с табличным (в специальных физических таблицах).
- Вычислите абсолютную и относительную погрешности экспериментального результата.
- Результаты измерений и вычислений занесите в таблицу (заполняйте ячейки только белого цвета!).
Название материала, из которого изготовлен брусок:
| Результаты измерений | Вычисления | |
| Длина бруска, a, см | ||
| Ширина бруска, b, см | ||
| Высота бруска, c, см | ||
| Масса тела, m, г | ||
| Объем, V, см3 | ||
| Плотность вещества, ρ , г/см3 | ||
| Табличное значение плотности, ρ , г/см3 | ||
| Абсолютная погрешность | ||
| Относительная погрешность |
Список литературы:
1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2010.- 395 с. - Глава 1, §3, п. 1, 3, 4, стр. 26 - 32.
Раздел 1. АЛГЕБРА И НАЧАЛА АНАЛИЗА
Тема 1.2. Корни, степени и логарифмы
Задание 4. Преобразование рациональных выражений. – 1 ч.
Цель: формирование умения выполнять преобразования рациональных выражений с использованием формул сокращённого умножения.
Задание для самостоятельной внеаудиторной работы:
& 4.1. Вспомните формулы сокращённого умножения. Что называют тождественными преобразованиями? Повторите, как выполнить сложение, вычитание, умножение, деление алгебраических дробей.
Основные сведения из теории:
4.2. Продолжите формулы сокращённого умножения:
1) 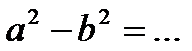
2) 
3) 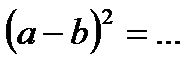
4) 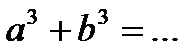
5) 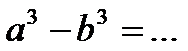
6) 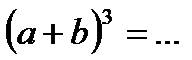
7) 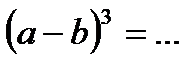
4.3. Выберите действия, которые относятся к тождественным преобразованиям:
· приведение подобных членов;
· раскрытие скобок;
· разложение на множители;
· умножение на отличное от нуля число;
· приведение алгебраических дробей к общему знаменателю.
Примеры и упражнения:
?4.4. Сократите дроби:
а) 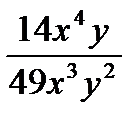 ; б)
; б) 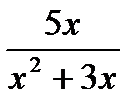 ; в)
; в) 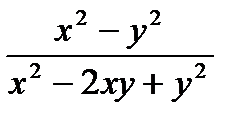 .
.
?4.5. Упростите выражения:
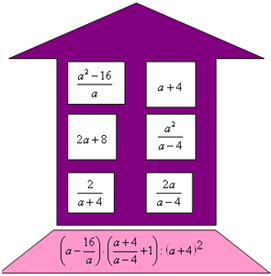 а)
а) 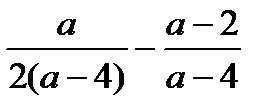 ; б)
; б) 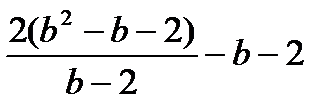 ; в)
; в)  ; г)
; г) 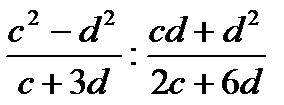 .
.
?4.6. Выполните действия:
а) 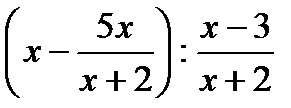 ; б)
; б) 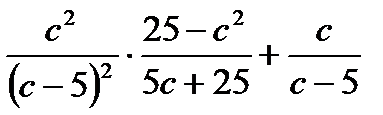 .
.
C4.7. Вы видите рисунок, изображающий ракету. В ракете есть 6 люков, в них записаны ответы каждого действия примера, приведённого снизу. Вычеркнув правильные ответы каждого действия, тем самым «закрыв люки», Вы получите изображение римской цифры. Назовите её.
¶ 4.8. Докажите тождество:
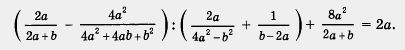
i4.9. Пройдите тесты на преобразование алгебраических выражений:
· http://grustlivaya.edusite.ru/p149aa1.html (умножение многочленов);
· http://grustlivaya.edusite.ru/p151aa1.html (формулы сокращённого умножения);
· http://grustlivaya.edusite.ru/p156aa1.html (формулы сокращённого умножения);
· http://reshuege.ru/test?theme=60&ttest=true;
· http://gorkunova.ucoz.ru/tests/1-6-0.
Список литературы:
1. Сайт «Алгебра, геометрия, физика» - сам себе репетитор (4 – 9 класс):
http://www.um100.ru/index.php?option=com_content&view=article&id=55&Itemid=53
Раздел 1. АЛГЕБРА И НАЧАЛА АНАЛИЗА
Тема 1.2. Корни, степени и логарифмы
Задание 5. Решение линейных, квадратных, рациональных уравнений. – 2 ч.
Цель: формирование умения решать линейные, квадратные, рациональные уравнения.
Задание для самостоятельной внеаудиторной работы:
& 5.1. Вспомните, что называют уравнением? Дайте определения корня уравнения. Что означает фраза «решить уравнение»? Какие уравнения называют линейными, квадратными, рациональными? Какова техника их решения?
Основные сведения из теории:
5.2. Закончите определения:
1) Уравнение- …, содержащее …
2) Корень уравнения- …, при подстановке которого уравнение обращается в …
3) Решить уравнение– значит найти все его … или доказать, что …
5.3. Заполните пропуски:
· Уравнение вида ах + в = 0, где а, в – заданные числа, 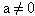 ; х – переменная, называется…
; х – переменная, называется…
· Метод решения линейных уравнений заключается в том, что …
· Уравнение вида ах2 + вх+ с = 0 где а, в, с – заданные числа, 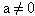 ; х – переменная, называется…
; х – переменная, называется…
· Квадратные уравнения бывают полными и …
· Корни полного квадратного уравнения находим через дискриминант, где D = …, по формуле 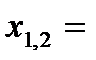 …
…
· Квадратное уравнение имеет два корня, если D = …
· Квадратное уравнение не имеет корней на множестве R, если D = …
· Полное квадратное уравнение имеет два равных корня, если D = …
· Метод решения неполного квадратного уравнения ах2 + вх = 0 заключается в том, что …
· Метод решения неполного квадратного уравнения ах2 + с = 0 заключается в том, что …
· Уравнение вида х2 + рх + q = 0 называется…
· Для решения приведённых квадратных уравнений можно использовать теорему …
· Теорема, обратная теореме Виета: Если числа 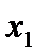 и
и 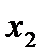 таковы, что их сумма равна …, а произведение равно …, то эти числа являются корнями уравнения …
таковы, что их сумма равна …, а произведение равно …, то эти числа являются корнями уравнения …
· Если … — рациональное выражение, то уравнение вида … называют рациональным.
· Метод решения рациональных уравнений заключается в том, что …
Примеры и упражнения:
?5.4. Решите уравнения, сводящиеся к линейным:
а) 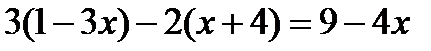 ; б)
; б) 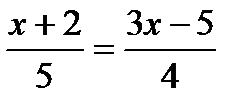 ; в)
; в) 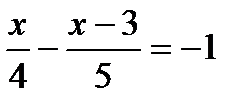 .
.
?5.5. Решите квадратные уравнения:
а) 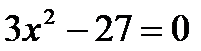 ; б)
; б)  ; в)
; в) 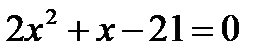 .
.
C5.6. Пусть х1 и х2 - корни квадратного уравнения. Используя теорему, обратную теореме Виета, заполните таблицу по образцу с учётом того, что х1<х2.
| Уравнение | Произведение корней | Сумма корней | х1 | х2 | Точка | Координаты |
| 1) х2-13х+22=0 | (х1; х2) | (2; 11) | ||||
| 2) х2-12х+35=0 | (х1; х2) | |||||
| 3) х2-10х+24=0 | (х1; х2) | |||||
| 4) х2-7х+12=0 | (х2; х1) | |||||
| 5) х2-11х+24=0 | (х2; х1) | |||||
| 6) х2-2х-8=0 | (х2; х1) | |||||
| 7) х2+6х+8=0 | (х1; х2) | |||||
| 8) х2+5х-24=0 | (х1; х2) | |||||
| 9) х2-5х+6=0 | (х1; х2) |
После решения уравнений точки с полученными координатами нанесите на координатную плоскость и последовательно их соедините. При правильном выполнении вы получите рисунок.
?5.7. Зная, что х1 и х2 - корни квадратного уравнения, применяя теорему Виета, составьте квадратные уравнения по образцу:
| № | х1 | х2 | х1+х2 | х1 ·х2 | Уравнение |
| 1. | -9 | -6 | -27 | 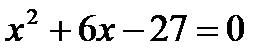
| |
| 2. | |||||
| 3. | -5 | -6 | |||
| 4. | 3-i | 3+i |
?5.8. Решите дробно-рациональные уравнения:
а) 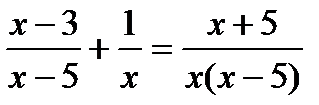 ; б)
; б) 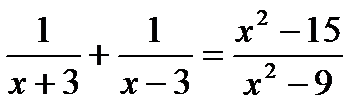 .
.
¶ 5.9. При каких k уравнение 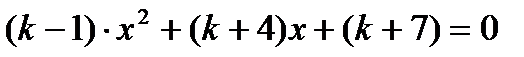 имеет ровно 1 корень?
имеет ровно 1 корень?
i5.10. Пройдите тесты на умение решать уравнения:
· http://grustlivaya.edusite.ru/p114aa1.html (линейные уравнения)
· http://www.ankolpakov.ru/testy-po-matematike-dlya-8-klassa-algebra-reshenie-kvadratnyx-uravnenij/ (квадратные уравнения);
· http://reshuege.ru/test?theme=14&ttest=true (линейные и квадратные уравнения);
· http://reshuege.ru/test?theme=9&ttest=true (рациональные уравнения);
· http://321start.ru/demo/demo.php (линейные, квадратные, дробно-рациональные уравнения).
Список литературы:
1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2010.- 395 с. - Глава 1, §5, п. 1, 2, стр. 39 – 42; глава 1, §8, п. 1 - 6, стр. 68 – 75.
Раздел 1. АЛГЕБРА И НАЧАЛА АНАЛИЗА
Тема 1.2. Корни, степени и логарифмы
Задание 6. Корень п-й степени и его свойства. – 1 ч.
Цель: формирование умения применять определение и свойства арифметического корня n–й степени.
Задание для самостоятельной внеаудиторной работы:
& 6.1. Вспомните, что называют арифметическим корнем n–й степени из числа а. Перечислите свойства арифметического корня n–й степени.
Основные сведения из теории:
6.2. Закончите определение:
Корнем n–й степени из числа а ( 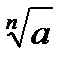 ) называют такое число, … степень которого равна …
) называют такое число, … степень которого равна …
6.3. Продолжите важные свойства корня n–й степени:
· 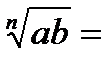 …
…
· 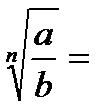 …
…
· 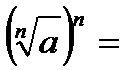 …
…
· 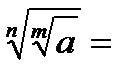 …
…
· 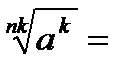 …
…
Примеры и упражнения:
?6.4. Вычислите:
а) 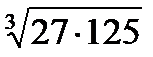 ; б)
; б) 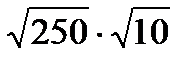 ; в)
; в) 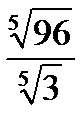 ; г)
; г) 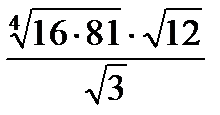 .
.
?6.5. Найдите значение выражения:
а) 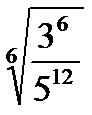 ; б)
; б) 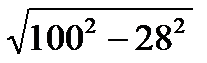 ; в)
; в)  ; г)
; г) 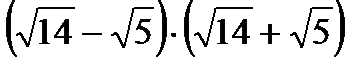 ; д)
; д) 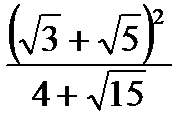 .
.
?6.6. Вынесите множители из-под знака корня:
а) 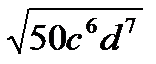 ; б)
; б) 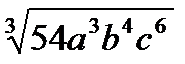 .
.
?6.7. Упростите выражение:
а) 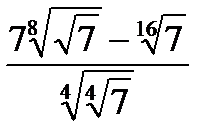 ; б)
; б) 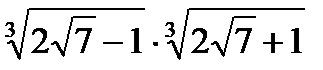 .
.
¶ 6.8. Вычислите:
а) 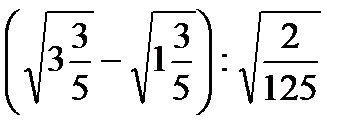 ; б*)
; б*) 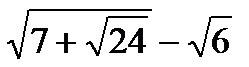 ; в)
; в) 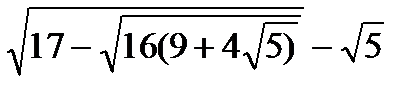 .
.
Указание: * - попробуйте выражение под квадратным корнем представить в виде 
i6.9. Пройдите тесты на умение преобразовывать выражения, содержащие корень п-й степени:
· http://reshuege.ru/test?theme=56&ttest=true;
· http://ipo.spb.ru/iumk2/MATH_XXI-10/Tests/Test_2.1.1/T_2.1.1.html.
Список литературы:
1. Башмаков М.И. Математика: учебник для 10 класса: среднее (полное) общее образование (базовый уровень) / М.И. Башмаков. - М.: Изд. центр "Академия", 2010. - 304с. – Глава 1, стр. 10 – 13.
2. Гипермаркет знаний – понятие корня п-й степени из неотрицательного числа. http://school.xvatit.com/.
Раздел 1. АЛГЕБРА И НАЧАЛА АНАЛИЗА
Тема 1.2. Корни, степени и логарифмы
Задание 7. Решение иррациональных уравнений. – 1 ч.
Цель: формирование умения решать иррациональные уравнения.
Задание для самостоятельной внеаудиторной работы:
& 7.1. Вспомните, какие уравнения называются иррациональными. Какова техника их решения?
Основные сведения из теории:
7.2. Закончите определение:
Уравнение, содержащее неизвестную переменную … называется иррациональным.
7.3. Продолжите высказывания:
· метод решения иррациональных уравнений – возведение …
· обязательными этапами решения являются запись … и выполнение …
Примеры и упражнения:
?7.4. Решите иррациональные уравнения:
а) 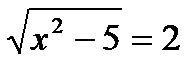 ; б)
; б) 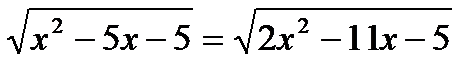 ; в)
; в) 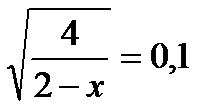 ; г)
; г) 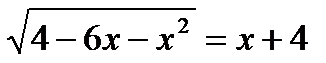 ;
;
д) 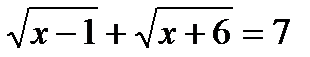 .
.
¶7.5. Решите иррациональные уравнения:
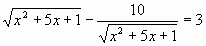 а)
а) 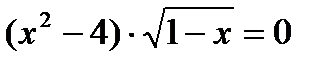 б)
б)
i7.6. Пройдите тест на решение иррациональных уравнений:
· http://reshuege.ru/test?theme=10&ttest=true.
Список литературы:
1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2010.- 395 с. - Глава 1, §11, п. 1, стр. 94 – 95.
Раздел 1. АЛГЕБРА И НАЧАЛА АНАЛИЗА
Тема 1.2. Корни, степени и логарифмы
Задание 8. Степень с натуральным, целым, рациональным, действительным показателем. – 2 ч.
Цель: формирование умения выполнять преобразования алгебраических выражений, содержащих степени с действительным показателем.
Задание для самостоятельной внеаудиторной работы:
& 8.1. Дайте определение степени числа а с натуральным, целым, рациональным показателем. Перечислите свойства степени.
Основные сведения из теории:
8.2. Закончите определение:
· 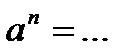 , где
, где 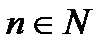 ;
;
· 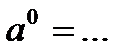 ;
;
·  , где
, где 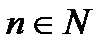 ;
;
· 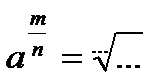 , где
, где 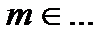 ,
, 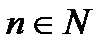 .
.
8.3. Продолжите основные свойства степени:
· 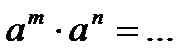 ;
;
· 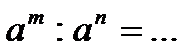 ;
;
· 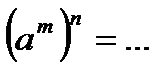 ;
;
· 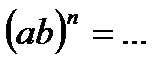 ;
;
·  ;
;
Примеры и упражнения:
При выполнении заданий по теме «Степень с натуральным, целым, рациональным, действительным показателем», мы будем обращаться к одному из драгоценных камней, который по блеску, красоте превосходит все минералы. Познакомимся с понятиями, которые используются в его добыче, обработке, с историей некоторых камней.
C8.4. Заполните таблицу:
| Буква | Пример | Ответ | Буква | Пример | Ответ | Буква | Пример | Ответ |
| Б | 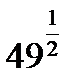
| Й | 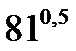
| З | 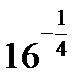
| |||
| Ы | 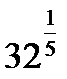
| С | 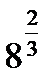
| О | 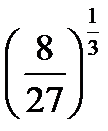
| |||
| Е | 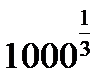
| Н | 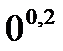
| А | 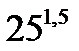
| |||
| П | 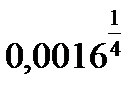
| Л | 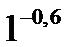
| М | 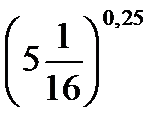
| |||
| И | 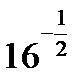
| Д | 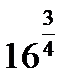
|

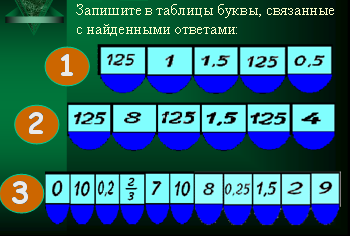 C8.5. Найдите значение выражений и заполните таблицу:
C8.5. Найдите значение выражений и заполните таблицу:
| Номер | Пример | Ответ | Буква | Номер | Пример | Ответ | Буква |
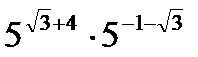
| 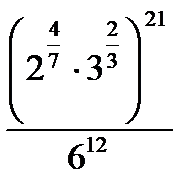
| ||||||
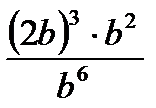 при b= 8 при b= 8
| 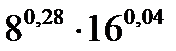
| ||||||
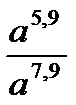 при a= 0,2 при a= 0,2
| 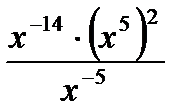 при х = 4 при х = 4
| ||||||
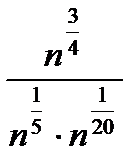 при n= 81 при n= 81
| 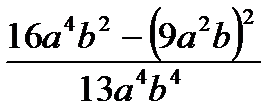 при a= -2, b= -5 при a= -2, b= -5
|

 C8.6. Заполните таблицу:
C8.6. Заполните таблицу:
| Выражение | Выражение в виде степени с рац. показателем | Слова |

| шатер | |
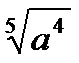
| павильон | |
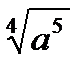
| остриё | |
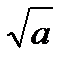
| коронка | |
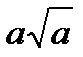
| плато | |
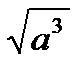
| арена | |
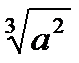
| площадка | |
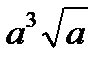
| крыша |


C8.7. Найдите значение выражений и заполните таблицу.
| Номер | Пример | Ответ | Название | Пример | Ответ = Масса |
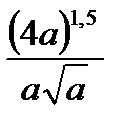 при a= 0,5 при a= 0,5
| 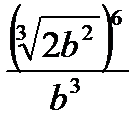 при b= 22 при b= 22
| ||||
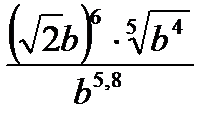 при b= при b= 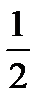
| 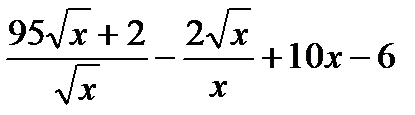 при х = 2 при х = 2
| ||||
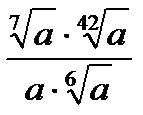 при a= 0,5 при a= 0,5
| 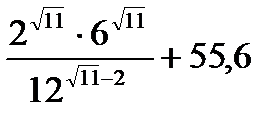
|
Выполнив это задание, Вы узнаете о самых знаменитых алмазах мира, у которых есть своя судьба.
Карта ответов (название алмаза):
| Екатерина | Царь Пётр | Меньшиков | Орлов | Кохинор | Шах |
| 0,5 |
 Масса драгоценных камней измеряется каратами: 1 карат = 0,2 г. Алмазы, имеющие массу более 53 карат, получают собственные имена. Наиболее крупные драгоценные камни России хранятся в Алмазном фонде страны, расположенном в Московском Кремле.
Масса драгоценных камней измеряется каратами: 1 карат = 0,2 г. Алмазы, имеющие массу более 53 карат, получают собственные имена. Наиболее крупные драгоценные камни России хранятся в Алмазном фонде страны, расположенном в Московском Кремле.
1) Одним из самых знаменитых бриллиантов является алмаз №1. Он был найден в Индии, затем попал в у «Персию», а в 1829 году был привезен в Россию в качестве выкупа за смерть А.С. Грибоедова.
 3) В алмазном фонде хранится еще один знаменитый бриллиант - №3. Он также был найден в Индии» в XVII веке и имел до огранки массу около 400 карат. После огранки бриллиант получил имя «Дерианур» - «море света». Алмаз неоднократно похищался, попадал в различные страны и к разным правителям. В 1773 году его приобрел фаворит Екатерины II Граф Григорий Орлов в дар императрице. Имя алмаза было изменено. Бриллиант был вставлен в Российский державный скипетр.
3) В алмазном фонде хранится еще один знаменитый бриллиант - №3. Он также был найден в Индии» в XVII веке и имел до огранки массу около 400 карат. После огранки бриллиант получил имя «Дерианур» - «море света». Алмаз неоднократно похищался, попадал в различные страны и к разным правителям. В 1773 году его приобрел фаворит Екатерины II Граф Григорий Орлов в дар императрице. Имя алмаза было изменено. Бриллиант был вставлен в Российский державный скипетр.
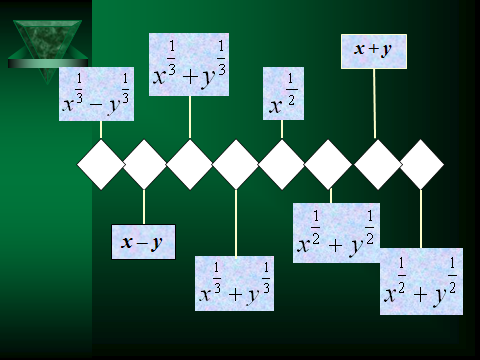
¶C8.8. Упростите выражение:
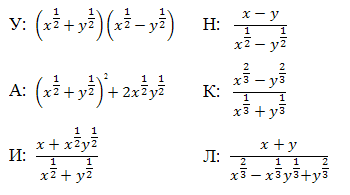
Упростив выражение, заполните пропуски на рисунке. Вы получите название крупнейшего в мире алмаза.
Долгое время основным местом добычи алмазов была Индия, а в начале XX века были открыты месторождения в Южной Африке. Там в 1905 году на одном из приисков был найден крупнейший алмаз, масса которого составляла 3106 карат, что равно 621 грамму. Он был назван именем хозяина прииска.
При огранке этот алмаз был рассечен на 9 частей. Наибольшая часть, имеющая массу 530 карат, была названа «Звезда Африки». Этот бриллиант, имеющий 74 грани, стал украшать британский державный скипетр.
i8.9. Пройдите тесты на умение выполнять действия со степенями:
· http://le-savchen.ucoz.ru/publ/4 (корни и степени - 3 теста);
· http://reshuege.ru/test?theme=61&ttest=true;
· http://reshuege.ru/test?theme=57&ttest=true;
· http://reshuege.ru/test?theme=62&ttest=true.
Список литературы:
1. Башмаков М.И. Математика: учебник для 10 класса: среднее (полное) общее образование (базовый уровень) / М.И. Башмаков. - М.: Изд. центр "Академия", 2010. - 304с. – Глава 1, стр. 13 – 16.
2. http://mirurokov.ru/otkrytyi-urok/25-vozvedenie-v-stepen/99-stepen-s-racionalnym-pokazatelem.html.
Раздел 1. АЛГЕБРА И НАЧАЛА АНАЛИЗА
Тема 1.2. Корни, степени и логарифмы
Задание 9. Решение показательных уравнений. – 1 ч.
Цель: формирование умения решать показательные уравнения.
Задание для самостоятельной внеаудиторной работы:
& 9.1. Вспомните, какие уравнения называются показательными. Какие основные методы решения показательных уравнений существуют?
Основные сведения из теории:
9.2. Закончите определение:
Уравнение, содержащее неизвестную переменную … называется показательным.
9.3. Продолжите высказывания:
Основными методами решения показательных уравнений являются:
· приведение обеих частей уравнения к …;
· вынесение за скобки …;
· введение … - метод …
Примеры и упражнения:
?9.4. Решите показательные уравнения методом приведения к одинаковому основанию:
а) 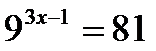 ; б)
; б) 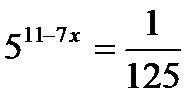 ; в)
; в) 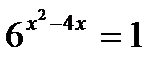 ; г)
; г) 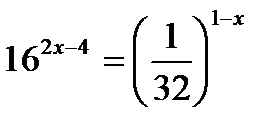 ; д)
; д) 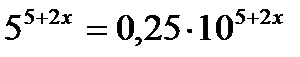 ;
;
е) 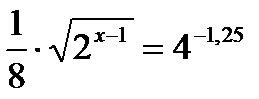 .
.
?9.5. Решите показательные уравнения, выбрав нужный метод решения:
а) 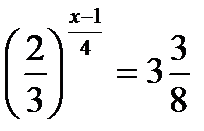 ; б)
; б) 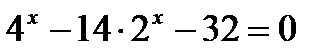 ; в)
; в) 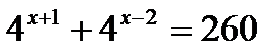 .
.
¶9.6. Решите показательные уравнения:
а)  ; б)
; б)  ; в)
; в) 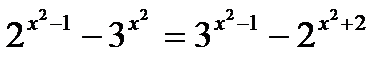 .
.
i9.7. Пройдите тесты на решение показательных уравнений:
· http://reshuege.ru/test?theme=11&ttest=true;
· http://le-savchen.ucoz.ru/publ/10-1-0-149.
Список литературы:
1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2010.- 395 с. - Глава 2, §18, п. 1, стр. 119 – 121.
Раздел 1. АЛГЕБРА И НАЧАЛА АНАЛИЗА
Тема 1.2. Корни, степени и логарифмы
Задание 10. Логарифм числа. Применение свойств логарифма. – 4 ч.
Цель: формирование умения вычислять логарифмы, использовать свойства логарифмов при преобразовании логарифмических выражений.
Задание для самостоятельной внеаудиторной работы:
& 10.1. Вспомните, что называют логарифмом числа b по основанию а. Какие основные свойства логарифма числа b по основанию а существуют?
Основные сведения из теории:
10.2. Закончите определение:
Логарифмом числа b по основанию а называют такой … , что …
Логарифм числа b по основанию … называют десятичным логарифмом числа b и обозначают …
Логарифм числа b по основанию … называют натуральным логарифмом числа b и обозначают …
10.3. Продолжите основные свойства логарифма числа b по основанию а:
1.  - основное логарифмическое тождество;
- основное логарифмическое тождество;
2. 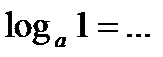 ;
;
3. 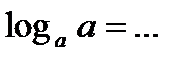 ;
;
4. 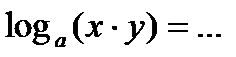 ;
;
5. 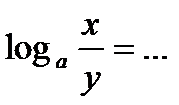 ;
;
6. 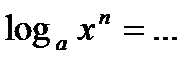 ;
;
7. 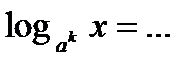 ;
;
8. 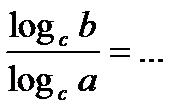 - формула перехода к новому основанию;
- формула перехода к новому основанию;
9. … = 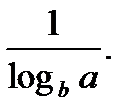
Примеры и упражнения:
?10.4. Заполните таблицу по образцу:
| № | Логарифм | Значение | Аргументация | № | Логарифм | Значение | Аргументация |
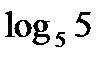
| 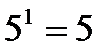
| 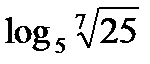
| |||||
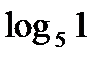
| 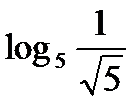
| ||||||
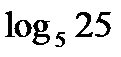
| 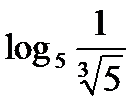
| ||||||
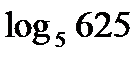
| 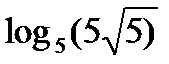
| ||||||
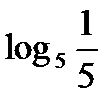
| 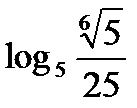
| ||||||
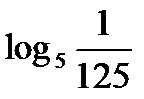
| 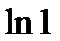
| ||||||
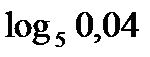
| 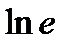
| ||||||
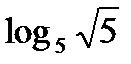
| 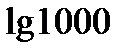
| ||||||
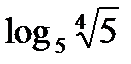
| 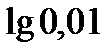
|
?10.5. Найдите значение выражения:
а) 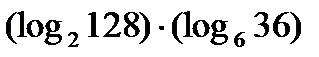 ; б)
; б) 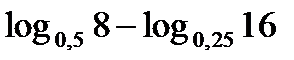 ; в)
; в) 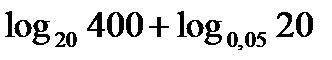 ; г)
; г) 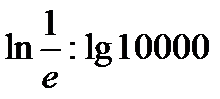 ; д)
; д) 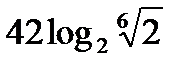 ; е)
; е) 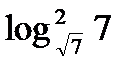 ; ж)
; ж) 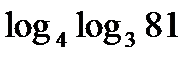 .
.
?10.6. Вычислите, используя свойства логарифма 4 -7:
а) 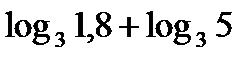 ; б)
; б) 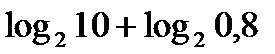 ; в)
; в) 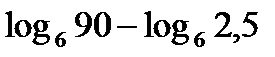 ; г)
; г) 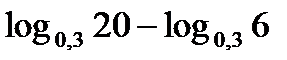 ; д)
; д) 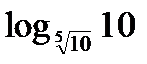 ; е)
; е) 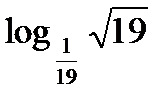 ; ж)
; ж) 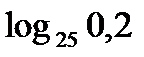 ; з)
; з) 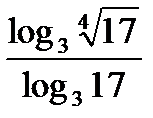 ; и)
; и) 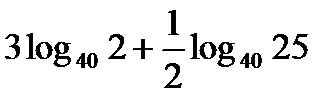 ; к)
; к) 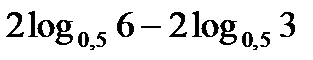 .
.
?10.7. Найдите число х по известному логарифму:
а) 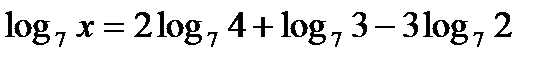 ; б)
; б)  .
.
¶10.8. Найдите значение выражения:
а) 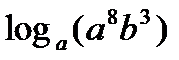 , если
, если 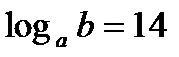 ; б)
; б) 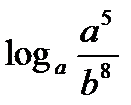 , если
, если 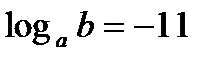 ; в)
; в) 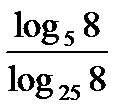 ;г)
;г) 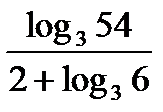 ; д)
; д) 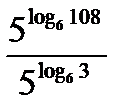 .
.
?10.9. Вычислите, используя свойства логарифма 8 - 9:
а)  ; б)
; б) 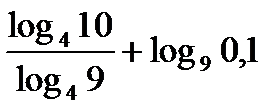 ; в)
; в) 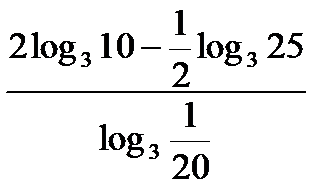 ; г)
; г) 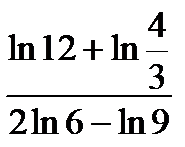 ; д)
; д) 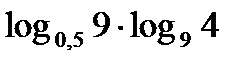 .
.
?10.10. Используя основное логарифмическое тождество, найдите значения выражений:
а) 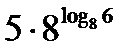 ; б)
; б) 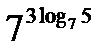 ; в)
; в) 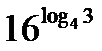 ; г)
; г) 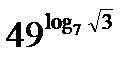 ; д)
; д) 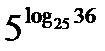 ; е)
; е)  ; ж)
; ж) 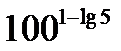 .
.
?10.11. Используя свойства логарифмов, найдите значения выражений:
а) 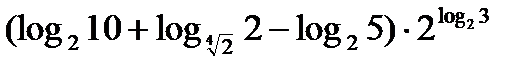 ; б)
; б) 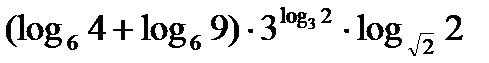 ;
;
в) 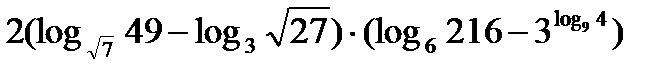 .
.
¶10.12. Найдите значение выражения:
а) 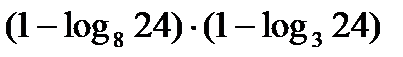 ; б)
; б) 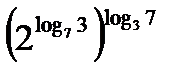 ; в)
; в) 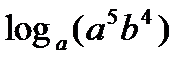 , если
, если 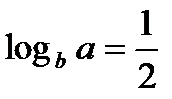 ;
;
г) 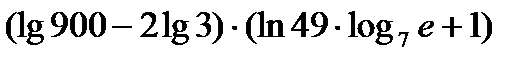 ; д)
; д)  .
.
i10.13. Пройдите тесты на преобразование логарифмических выражений:
· http://reshuege.ru/test?theme=58;
· http://reshuege.ru/test?theme=63;
· http://le-savchen.ucoz.ru/publ/12-1-0-93;
· http://le-savchen.ucoz.ru/publ/12-1-0-92;
· http://le-savchen.ucoz.ru/publ/12-1-0-91;
· http://le-savchen.ucoz.ru/publ/12-1-0-90.
Список литературы:
1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2010.- 395 с. - Глава 2, §18, п. 1, стр. 119 – 121.
2. Башмаков М.И. Математика: учебник для 10 класса: среднее (полное) общее образование (базовый уровень) / М.И. Башмаков. - М.: Изд. центр "Академия", 2010. - 304с. – Глава 1, стр. 16 – 21.
Раздел 1. АЛГЕБРА И НАЧАЛА АНАЛИЗА
Тема 1.2. Корни, степени и логарифмы
Задание 11. Решение логарифмических уравнений. – 1 ч.
Цель: формирование умения решать логарифмические уравнения.
Задание для самостоятельной внеаудиторной работы:
& 11.1. Вспомните, какое уравнение является логарифмическим. Перечислите основные методы решения логарифмических уравнений.
Основные сведения из теории:
11.2. Закончите определение:
Уравнение, содержащее неизвестную переменную … называют логарифмическим.
11.3. Продолжите высказывания:
Основными методами решения логарифмических уравнений являются:
· по …;
· приведение обеих частей уравнения к … - ...;
· введение … - метод …
При решении логарифмических уравнений необходимо выписать … и сделать … решения.
Примеры и упражнения:
?11.4. Решите логарифмические уравнения по определению:
а) 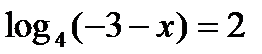 ; б)
; б) 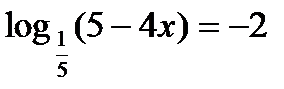 ; в)
; в) 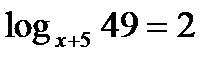 .
.
?11.5. Решите логарифмические уравнения методом потенцирования:
а)  ; б)
; б) 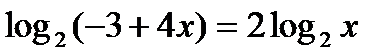 .
.
?11.6. Решите логарифмические уравнения, выбрав нужный метод решения:
а) 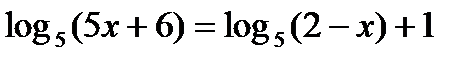 ; б)
; б) 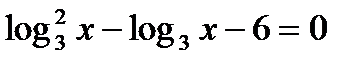 .
.
¶11.7. Решите логарифмические уравнения:
а) 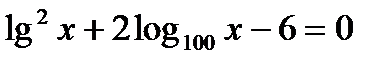 ; б)
; б) 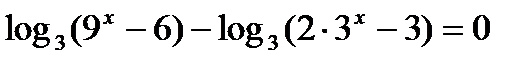 ; в)
; в) 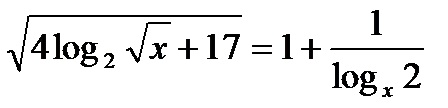 .
.
i11.8. Пройдите тест на решение логарифмических уравнений:
· http://reshuege.ru/test?theme=12&ttest=true.
Список литературы:
1. Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов, П.И. Самойленко. – М.: Дрофа, 2010.- 395 с. - Глава 2, §20, п. 1, стр. 123 – 124.
Раздел 1. АЛГЕБРА И НАЧАЛА АНАЛИЗА
Тема 1.2. Корни, степени и логарифмы
Задание 12. Итоговое повторение по теме 1.2. – 1 ч.
Цель: формирование умения проводить преобразования выражений, включающих степени, радикалы, логарифмы; находить значения корня натуральной степени, степени с рациональным показателем, логарифма; решать иррациональные, показательные, логарифмические уравнения.
Задание для самостоятельной внеаудиторной работы:
& 12.1. Вспомните основные свойства степени и логарифма, основные виды уравнений и методы их решений.
Основные сведения из теории:
12.2. Для успешного прохождения теста вспомните основные понятия и формулы, изученные в теме «Корни, степени и логарифмы». Заполните пропуски:
№1. 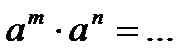 ;
; 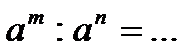 ;
; 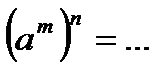
№2. Корнем n–й степени из числа а ( 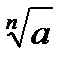 ) называют такое число, … степень которого равна …
) называют такое число, … степень которого равна … 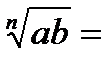 …
…
№3. 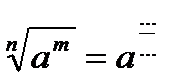 ,
, 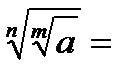 …
…
№4. Метод решения иррациональных уравнений – возведение … Обязательными этапами решения являются запись … и выполнение …
№5.Один из методов решения показательных уравнений - приведение обеих частей уравнения к … Если в показательном уравнении основания степени равны, то и показатели степени …
№6. 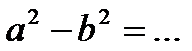
№7. Логарифмом числа b по основанию а называют такой … , что …
№8. Логарифм числа b по основанию … называют десятичным логарифмом числа b и обозначают … Логарифм числа b по основанию … называют натуральным логарифмом числа b и обозначают …
№9. 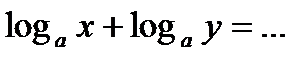 ;
; 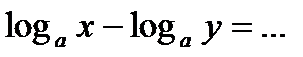 ;
; 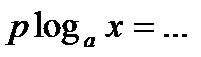 ;
; 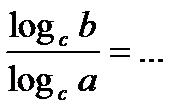
№10.  - основное логарифмическое тождество.
- основное логарифмическое тождество.
№11. Один из методов решения логарифмических уравнений является использование определения логарифма числа b по основанию а. При решении логарифмических уравнений необходимо выписать … и сделать … решения.
№12. 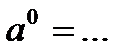 ;
;  .
.
Примеры и упражнения:
?12.3. Пройдите тест (в случае возникновения трудностей,
| <== предыдущая страница | | | следующая страница ==> |
| САМОСТОЯТЕЛЬНОЙ РАБОТЫ | | | ЛОГАРИФМ И ЕГО СВОЙСТВА |
Дата добавления: 2014-10-14; просмотров: 1441; Нарушение авторских прав

Мы поможем в написании ваших работ!